konsp_lektsiy_1ch

2

УДК 62(07)

Конспект лекций по дисциплине «Основы теории сооружений» Часть 1 (для студентов дневной формы обучения специальности 8.06010201

Архитектура зданий и сооружений ) / Сост. Денисов Е.В., Руднева И.Н. – ПЦ ДонНАСА, 2013. – 52 с.

Конспект лекций по курсу «Основы теории сооружений» предназначен для студентов специальности для студентов дневной формы обучения специальности 8.06010201 «Архитектура зданий и сооружений» и включает в себя основные теоретические сведения из трех дисциплин: теоретической механики, сопротивления материалов, строительной механики. Теоретический материал иллюстрируется рисунками, приводятся основные уравнения и расчетные формулы, а также примеры решения задач.

3

СОДЕРЖАНИЕ

ЛЕКЦИЯ № 1. ЗАДАЧИ КУРСА "ОСНОВЫ ТЕОРИИ СООРУЖЕНИЙ". КОРОТКИЙ

ЛЕКЦИЯ № 6. ПОПЕРЕЧНЫЙ ИЗГИБ БРУСА. ВНУТРЕННИЕ УСИЛИЯ, ПОНЯТИЕ

4

ЛЕКЦИЯ № 7. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ. РАЦИОНАЛЬНОЕ

СЕЧЕНИЕ БАЛОК. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ. АНАЛИЗ

7.4.АНАЛИЗНАПРЯЖЕННОГОСОСТОЯНИЯ ПРИИЗГИБЕНА ПРИМЕРЕ БАЛКИПРЯМОУГОЛЬНОГО

5

ЛЕКЦИЯ № 1. ЗАДАЧИ КУРСА "ОСНОВЫ ТЕОРИИ СООРУЖЕНИЙ". КОРОТКИЙ ИСТОРИЧЕСКИЙ ОБЗОР. ОСНОВНЫЕ ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ ПЕРЕРЕЗОВ. СОРТАМЕНТ ПРОКАТНЫХ ПРОФИЛЕЙ

1.1.ВВЕДЕНИЕ. РОЛЬ КУРСА В РАБОТЕ АРХИТЕКТОРА

Окружающий нас мир наполнен творениями рук и ума человека. Это машины, самолеты, корабли, высотные здания, мосты, плотины, нефтепроводы и т. д. Все это принято называть конструкциями. Основной задачей архитекторов и строителей в процессах проектирования и строительства зданий и сооружений является обеспечения прочности и долговечности конструкций. Известно много памятников архитектуры, которые пережили тысячелетие и сохранили достаточную прочность. Давнишние строители старались придать своим сооружениям большие запасы прочности, устраивая их слишком толстыми стенами, массивными колонами. К сожалению, сохранилось немного сведений о том, как определялись размеры элементов сооружений. Древние сооружения не отличались конструктивным разнообразием: строители копировали старые, проверенные временем конструктивные формы. Конструктивные изменения закреплялись в строительной практике очень медленно. При современном развитии техники и большому разнообразию типов сооружений уже нельзя в строительстве полагаться на время: сейчас необходимо строить быстро, прочно и экономично.

При проектировании конструкций необходимо определить внешние нагрузки, которые будут действовать на них, выяснить законы изменения внутренних усилий в разных частях конструкции, и подобрать размеры элементов этой конструкции так, чтобы все они были крепкие и не имели слишком больших запасов несущей способности.

Равновесие и движение сооружений или их элементов и методы их расчетов на прочность, жесткость и устойчивость изучает наука “Теория сооружений”.

Равновесие тела – это состояние относительного покоя или состояние, при котором все точки тела перемещаются равномерно и прямолинейно.

Абсолютно твердое тело – это такое тело, у которого расстояния между всеми его точками при любом механическом воздействии остаются неизменными.

Курс “Основы теории сооружений” состоит из нескольких дисциплин:

а) теоретической механики, б) сопротивления материалов, в) строительной механики.

Объектами изучения этих дисциплин в рамках настоящего курса являются абсолютно твердое тело, стержень, стержневые конструкции.

Все перечисленные дисциплины не задевают вопроса о внутреннем строении тела, но базируются на экспериментально проверенных предположениях (гипотезах), что учитывают их физические свойства.

Теоретическая механика изучает равновесие и движение твердого тела; состоит из трех частей: статики, кинематики, динамики. Сопротивление материалов и строительная механика изучают методы расчетов на прочность, жесткость и устойчивость соответствующих конструкций.

1.2. КРАТКИЙ ИСТОРИЧЕСКИЙ ОЧЕРК

Наука о поведении материалов под нагрузкой, очевидно, возникла тогда, когда у человека появилась потребность в создании сложных сооружений, постройке больших морских судов. Точно назвать такую дату нельзя. Первые сооружения - египетские пирамиды Хеопса высотой 145 метров были построены 1000 лет до новой эры. Мы не перестаем удивляться мастерству древних строителей, воздвигших прекрасные акведуки в Древнем Риме, дворцы в Византии, храмы в Древней Руси, культовые сооружения Востока.

7

Рассмотрим некоторое произвольное поперечное сечение стержня (рис. 1.1), помещенного в систему координат (x, y). Выделим в сечении элемент бесконечно малой площади dF 0. Положение такой площадки будет характеризоваться координатами (x, y). Расстояние от центра координат до площадки – полярный радиус, обозначим .

Рис.1.1.

Статическими моментами площади F относительно осей x и y называются величины Sx и Sy , определяющиеся по формуле:

Осевыми моментами инерции площади F относительно осей x и y называются величины Ix и Iy, определяющиеся по формуле:

Центробежным моментом инерции площади F относительно системы осей (x, y) называется величина Ix y, определяющаяся по формуле:

В связи с тем, что в формулах (1.2), (1.4) под интегралом находятся квадраты координат, значения осевых моментов инерции площади и полярные моменты инерции площади всегда будут положительными. Статические моменты инерции и центробежный момент инерции площади могут иметь любой знак и могут быть равными нулю.

При этом, поскольку 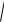x2 y2 , полярный момент инерции площади может быть найден как сумма осевых моментов инерции площади:

FF

Всоответствии с приведенными формулами (1.1)-(1.4) единицами измерения

статических моментов площади являются Sx, Sy [см3], осевых, центробежного и полярного моментов инерции площади - Ix, Iy, Ix y, I [см4].

Помимо приведенных выше основных геометрических характеристик следует познакомиться еще с несколькими производными характеристиками, которые также используются в расчетах на прочность и устойчивость.

Моментами сопротивления площади F относительно осей x и y называются величины Wx и Wy, равные отношению соответствующих моментов инерции Ix, Iy к координатам точек сечения уmax, xmax, максимально удаленных от данной оси:

9

Моменты сопротивления площади (1.14) прямоугольного сечения:

Радиусы инерции площади (1.15) прямоугольного сечения:

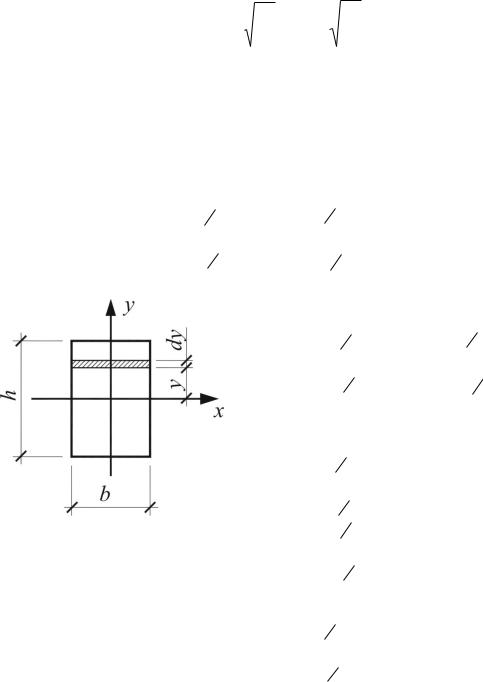
Иногда для получения геометрических характеристик удобно использовать полярную систему координат, как, например, в случае с круглым сечением (рис.1.4). В соответствии с (1.4) Полярный момент инерции площади (1.13) круглого сечения определится как:

В соответствии с (1.5) осевые моменты инерции площади (1.11) определятся как:

1.4. СОРТАМЕНТ ПРОКАТНЫХ ПРОФИЛЕЙ

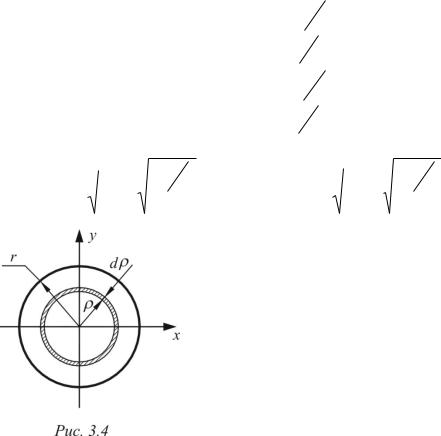
Изучение расчетов элементов конструкций будем производить на основе наиболее простого случая материала стержня – металлического стержня. Большинство металлов и сплавов являются изотропными материалами, что существенно облегчает расчет. Наиболее распространенный в строительной практике металл – это сталь. Сталью является сплав железа с углеродом. Доля углерода в стали и процентное содержание различных химических соединений и элементов, обуславливают наличие сталей разных марок по своим характеристикам. Для изготовления стержневых элементов применяются прокатные профиля, т.е. профиля полученные в заводских условиях способом прокатки. Основными прокатными профилями, применяющимися в строительстве, являются: двутавры, швеллера, уголки, листы, трубы, круги и квадраты. Номенклатура сечений этих профилей приведена в соответствующих ГОСТах (ДСТУ) и называется сортаментом.

Сортаментом прокатных профилей называется совокупность профилей по форме их поперечного сечения и размеров, которые изготавливаются в заводских условиях способом прокатки. Современный архитектор обязан знать и различать основные типы прокатных профилей, представленных в табл. 1.1.

10

Основные типы прокатных профилей

Таблица 1.1