
- •Лабораторная работа № 9 Вычисление корней уравнения методом деления отрезка пополам
- •I. Организационный момент
- •II. Мотивационное начало урока. Постановка цели урока
- •III. Изучение нового материала.
- •IV. Этап закрепления, проверки полученных знаний
- •V. Задания для самостоятельного выполнения
- •Пример: класс для решения уравнения методом деления отрезка пополам (метод бисекции, он же, метод дихотомии)
- •1. Краткое описание сущности метода касательных
- •2. Решение нелинейного уравнения аналитически
- •3. Блок схема программы
- •4. Программа на языке pascal7.0
- •5. Результаты выполнения программы
Лабораторная работа № 9 Вычисление корней уравнения методом деления отрезка пополам
Время проведения: первый урок по теме “Приближенные вычисления”
Цели урока:
Развитие представлений о применениях ЭВМ для научно-технических расчетов.
Формирование системно-информационного подхода к анализу окружающего мира.
Формирование общеучебных и общенаучных навыков работы с информацией.
Задачи урока:
Воспитательная – развитие познавательного интереса, воспитание информационной культуры, воспитание умения четко организовать самостоятельную работу.
Образовательная – изучить и закрепить приемы использования языка программирования для решения задач приближенного решения уравнений, закрепить знания и умения по теме “Алгоритмизация и программирование”.
Развивающая – расширение кругозора.
Методы: Словесные, наглядные, практические.
Организационные формы работы: фронтальные, индивидуальные.
Материально-техническая база: доска, ПК с установленным ПО ЯП Turbo Pascal 7.0.
Межпредметная связь: математика.
Требования к знаниям и умениям: учащиеся должны знать основные команды языка программирования для задач вычислительного характера, уметь составлять и записывать алгоритмы с использование циклов и ветвлений; по записи алгоритма записывать программу на языке программирования Turbo Pascal.
План урока:
|
Содержание этапа урока |
Вид и формы работы |
|
1. Организационный момент |
Приветствие |
|
2. Мотивационное начало урока. |
Постановка цели урока. |
|
3 Изучение нового материала. Ознакомление с новым методом приближенного решения уравнений, показ образца действий. |
Работа в тетради. |
|
4. Закрепление и проверка полученных знаний. |
Фронтальный опрос. Работа у доски. Работа в тетради по кодированию программ по заданному алгоритму. |
|
5. Упражнения творческого характера. |
Лабораторная работа: применение созданной программы для приближенного вычисления корня функции. Работа в тетради. Защита результатов. |
|
6 Подведение итогов урока, домашнее задание. |
Работа в тетради. |
ХОД УРОКА
I. Организационный момент
II. Мотивационное начало урока. Постановка цели урока
Учитель:
Вычисления
на компьютере обладают большей гибкостью,
чем привычные всем вычисления в
математике. Рассмотрим для примера
задачу вычисления корня уравнения f(x)
= 0. В курсе школьной математики вам
известен метод дискриминанта для
уравнений вида:
ax2
+ bx
+ c
= 0, выражаемой по формуле
![]() .
Однако, во многих случаях, ответ не
выражается формулой (например, для корня
уравненияcos(x)
= x
формулы просто нет). Но можно, не выводя
точных формул, вычислить корень
приближенно, с заданной точностью,
например, до 0,0001. Сегодня мы рассмотрим
один из приближенных методов вычисления
корня уравнения – метод деления отрезка
пополам.
.
Однако, во многих случаях, ответ не
выражается формулой (например, для корня
уравненияcos(x)
= x
формулы просто нет). Но можно, не выводя
точных формул, вычислить корень
приближенно, с заданной точностью,
например, до 0,0001. Сегодня мы рассмотрим
один из приближенных методов вычисления
корня уравнения – метод деления отрезка
пополам.
III. Изучение нового материала.
Учитель: Рассмотрим задачу в следующей постановке.
Дано уравнение f(x) = 0 и числа a и b: a < b, f(a) и f(b) имеют разные знаки на отрезке [a, b], т.е. f(a)* f(b)<0, а график функции y = f(x) есть непрерывная линия на отрезке [a, b]. В этом случае график функции обязательно пересечет ось OX. (См. рис 1).

Рисунок 1
Требуется определить корень уравнения W с точностью E > 0.
Если V–точный корень уравнения f(V) = 0, a < V < b, то требуется найти W: |W – V| < E, a < W < b.
При такой постановке алгоритм метода деления отрезка пополам следующий:
1) c = (a + b)/2 {вычисляем середину отрезка [a, b]}
2) если f(a) * f(b) < 0, то b = c иначе a = c. {выбираем левую или правую часть отрезка, где находится корень уравнения}
3) если |a – b| > E, то перейти к пункту 1). {если величина длины отрезка не достигла требуемой точности, то процесс деления отрезка продолжаем}
Любая точка отрезка [a, b] при таком алгоритме даст приближенное решение с заданной точностью.
Запишем алгоритм решения нашей задачи в виде блок схемы: (См. рис. 2).
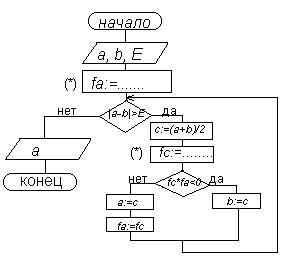
Рисунок 2
Учитель: Есть ли вопросы?
Если у учащихся есть вопросы, то необходимо все уяснить, прежде чем переходить к следующему этапу урока/
Учитель: Какой алгоритм по структуре у нас получился?
ПО: циклический, причем использовать надо цикл с предусловием.
Учитель: Что необходимо вписать в блоки, помеченные звездочкой ( * )?
ПО: Здесь необходимо записать команду вычисления конкретной функции в точке a и в точке c.
Учитель: Что необходимо предварительно сделать, прежде чем применять этот алгоритм для нахождения корня уравнения?
ПО: Необходимо, в первую очередь, проверить, удовлетворяет ли функция постановке задачи: является ли график функции непрерывной линией на отрезке [a, b], разные ли знаки имеет функция на концах отрезка [a, b].
