Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Евразийский национальный университет им. Л.Н. Гумилёва

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3lk_0

.pdf

Скачиваний:

Добавлен:

21.02.2016

Размер:

1.38 Mб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

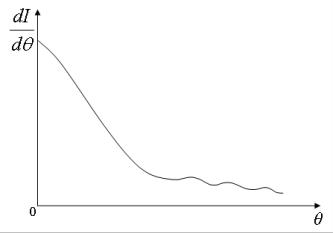
чередующиеся максимумы и минимумы в соответствии с длиной волны движущего электрона, равной λ= h/Pe.

Рис.4. Зависимость интенсивности рассеянных электронов от угла рассеяния от монокристалла никеля

Вскоре, эффекты дифракции наблюдались в рассеянии более тяжѐлых частиц нейтронов ( mn 2000me ), а также ионов и даже молекул, для

которых соответствующие λ были очень маленькие.

Дуальность света в природе уравновешивается дуальностью движущихся частиц, которые в определенных случаях проявляют себя как волны.

Резюме

Таким образом, для описания движения микрочастиц нельзя использовать механику, так как с еѐ помощью нельзя объяснить дифракцию и интерференцию, но нельзя было использовать и волновую теорию, которая не объясняла корпускулярные свойства частиц (перенос вещества, заряда). Необходима была новая теория: волновая механика частиц или квантовая механика волн.

Математический аппарат квантовой механики

Исааку Ньютону при создании своей механики потребовался математический аппарат – дифференциальное исчисление. Законы квантовой механики могут быть сформулированы и лучше усвоены с помощью своей математики – математики операторов.

Понятие оператора. Свойства операторов

Определение1. Оператором ˆ называется правило, закон, рецепт, с

помощью которого каждой функции	f, из некоторого класса функций,
ставится в соответствие другая функция φ, что обозначается так:
ˆ	.	(1)
Af

Операторы будем обозначать большими буквами со “шляпкой”. Равенство

(1) читается: оператор ˆ переводит функцию f в φ.

Примеры. Рассмотрим оператор дифференцирования:

		ˆ		d			f x arctg x ;
		A		dx		и	f x arctg x ;
	d							1
		arctg x			arctg x				.
	dx	arctg x			arctg x			1 x2	.
Другой оператор – умножения:
			ˆ		ˆ		ˆ
			A x ;				xf x xf x .

Не на всякую функцию можно действовать всяким оператором. В первом примере f(x) должна быть дифференцируемой. Поэтому, когда задают оператор, указывают класс функций, на которые он действует.

Опеределение 2. Оператор считается заданным, если наряду с правилом, законом, указано множество функций, на которые действует этот оператор.

Такое множество называется областью определения оператора.

	ˆ	ˆ
Определение 3. Произведением двух операторов A		и B называется оператор
ˆ	ˆ
A B , действие которого на функцию сводится к последовательному
	ˆ	ˆ
действию сначала оператора B , а потом оператора		A на результат действия

B или:

(2)

A B f

A B f .

Пример:

dx ,

B x ;

A B f x

xˆf x x f x

f x xf x 1

xˆ

f x ,

или можно получить произведение операторов (эквивалентный оператор):

ˆ ˆ		d
A B	1 xˆ		.
		dx

Изменим порядок действия этих операторов:

ˆ	ˆ	d
B A f x xˆ		dx
		dx

или:

		x f (x) (xˆ			d
f	x					) f x	,
f	x					) f x
					dx
					dx
ˆ	ˆ		d
B A		xˆ	dx	.

Поэтому, в общем случае операторы нельзя переставлять местами

		ˆ	ˆ		ˆ	ˆ				(3)
		A	B		B	A.				(3)
	Для произведения одинаковых операторов используют для краткости
обозначения:
			ˆ	ˆ		ˆ 2	,
			A A			A	,
		ˆ	ˆ	ˆ	ˆ		ˆ n			(4)
		A A		A...A			A			(4)
							ˆ	ˆ
Определение 4. Суммой двух операторов A								и B называется оператор
ˆ	ˆ
A ±	B , который действует на функцию f следующим образом:
		ˆ		ˆ			ˆ	ˆ		(5)
		( A ±		B ) f =			A f ± B f.			(5)
	ˆ	ˆ	ˆ	ˆ				ˆ	ˆ	(оператор
Операторы равны, A =		B , если (	A − B ) f = 0 или A − B =0							(оператор
умножения на ноль).
Определение 5. Выражение вида:
		ˆ	ˆ		ˆ	ˆ		ˆ ˆ		(6)
		A B − B ∙ A =						A, B		(6)
						ˆ		ˆ	ˆ ˆ

называется коммутатором операторов A и B . Если A, B =0, то говорят, что

операторы коммутируют. В противном случае операторы не коммутируют.

d		ˆ
Самостоятельно. Показать, что	, xˆ	1 .

dx

Операторы “набла” и дельта

Операторы в квантовой механике могут быть векторными, как, например, оператор - набла, который определѐн на дифференцируемых функциях трѐх переменных:

i		j		k		,	(7)
	x		y		z

где i, j, k – единичные, взаимно ортогональные векторы.

Под произведением двух векторных операторов будем подразумевать их скалярное произведение, если не оговорено противное:

2	2	2	2	.
					(8)
	x2	y2	z2

Полученный оператор носит название оператора Лапласа и обозначается греческой буквой . Он определѐн на функциях трѐх переменных, имеющих вторые частные производные. Заметим, что функции

в квантовой механике могут быть и комплексными, так же, как и операторы.

Например:

xˆ i	d		1 d 2

	dx	,		i dx	2 .
		,			2 .

Свойства квантовомеханических операторов

В дальнейшем будем иметь дело со специальными операторами, а

именно: линейными и самосопряжѐнными (эрмитовыми).

Определение 6. Оператор ˆ называется линейным, если:

ˆ	C2 f	ˆ	ˆ	,
A C1 f1	C2 f	2 C1 Af1	C2 Af2	,

где С1 и С2 – числа, а f1 и f2 – функции, на которых определѐн оператор

Пример: покажем, что оператор A

– линейный оператор:

df1

df2

C1 f1 (x) C2

f2 (x) C1 f1 (x)

C2 f

2 (x)

Для доказательства использованы правила дифференцирования.

Определение 7. Самосопряжѐнным или эрмитовым называется

(9)

A .

такой

ˆ			функциях		f1(x), f2(x), для	которого
оператор A , определѐнный на
выполняется равенство:
*	ˆ	(x)dx	f	ˆ * *	(x)dx ,	(10)
f1	(x) Af2			2 (x) A f1

где (*) обозначает комплексное сопряжение функции и оператора, x – совокупность непрерывных переменных, которых может быть больше, чем

одна, например, x x1 , x2 , x3 , x4 . Интеграл (10) − или определѐнный, или

многократный, поэтому пределы интегрирования здесь и в дальнейшем не конкретизируются. Не все операторы самосопряжѐнные, например, оператор

– несамосопряжѐнный.

Докажем

это.

Пусть

f1(x) и

f2(x) −

дифференцируемые

функции,

определѐнные

на

отрезке

[a,b],

удовлетворяющие условию:

a f1 b ;

f2 a f2 b .

Запишем определѐнный интеграл:

I1 f1

2 x dx ,

и ещѐ один:

f x

f * x dx.

Если оператор dx самосопряжѐнный, то по определению (10) I1 = I2

f *

x dx f x f * x

I f

f * x f x dx b

f * x

* f x dx I

Докажем, что оператор Β i

– эрмитов. Для доказательства будем

использовать те же функции:

* x

x dx

;

~	b				d *
I2		f2		i
I2		f2	x	i	dx
	a				dx

i f1* x f2 x dx

f1* x dx i f2 x f1* x b

b			d			~
	f * x	i		f		x dx I		.
	f * x	i		f		x dx I		.
	1				2		1
a			dx

Итак, оператор ˆ d и линейный, по ранее доказанному, и

Β i dx

самосопряжѐнный.

2 d

Самостоятельно. Проверить, будет ли эрмитов оператор i dx ?

Собственные функции и собственные значения операторов и их свойства. Вырожденные функции

После действия оператора на функцию получается, вообще говоря, другая функция. Но, иногда, функция, после действия на неѐ оператора изменяется не существенно, а лишь на постоянный множитель.

В общем виде такое “действие”оператора на функцию можно записать:

			ˆ	af ,	(11)
			Af	af ,	(11)
где a – число.
Пример.
ˆ	d 2
A			, f x cos 3x ,
A	dx	2	, f x cos 3x ,
	dx

dxd 22 cos(3x) cos3x 9cos 3x .

в операторном уравнении (11)

Определение 8. Величина a в уравнении (11) носит название собственного

значения оператора ˆ . Соответствующая этому собственному значению

функция f, обозначаемая обычно

f fa ,

называется собственной функцией оператора ˆ , принадлежащая

собственному значению a.

Совокупность собственных значений оператора ˆ называется

спектром собственных значений этого оператора, который может быть непрерывным, в конечном интервале или нет:

a0	a b0	,	(12)
a .			(12)
a .

Если оператор ˆ задан, то условие (11) можно рассматривать как

уравнение для нахождения собственных функций.

Пример.

ˆ d ,

A i dx

то:

if x a f x .

Решая это дифференциальное уравнение с разделяющимися переменными, получаем:

f x fa x C e iax ,

где C > 0, а в остальном произвольная константа. Замечание. Собственные функции fa x

определены только с точностью до произвольного множителя. Самостоятельно. Показать, что функция 25e-iax также будет собственной

ˆ	d
функцией оператора A i		.
функцией оператора A i	dx	.
	dx

Определение 8*. Если уравнение (11) имеет решение не при всех значениях a, а только некоторых an (n = 1, 2, 3, …), то спектр собственных значений становится дискретным конечным, или нет:

a1 , a2 , a3 , , an ,		,	(13)
а само уравнение приобретает вид:
ˆ	an fn ,		(11)*
Afn	an fn ,		(11)*
n – натуральные числа.
ˆ			могут быть
Так как оператор A и его собственные функции f			могут быть

комплексными, то комплексными могут быть и собственные значения a операторов.

Теорема 1. Если оператор ˆ самосопряжѐнный, то его собственные

значения a – вещественные.

Доказательство. Пусть:
ˆ	x afa x .	(14)
Afa
Умножим это уравнение слева на	fa* x и проинтегрируем левую и правую

части полученного равенства по x в заданных пределах (без их указаний):

fa x Afa x dx a

fa x fa

x dx a

fa x

dx.

(14а)

Перепишем (14) в виде:

ˆ * *

A fa

x a

fa ;

умножим это равенство слева на

x и также проинтегрируем по x:

ˆ *

x dx

fa x

dx .

fa x A

(14б)

Так как ˆ – самосопряжѐнный оператор, то левые части равенства (14а) и

(14б) равны, а правые отличаются только множителями, отсюда a = a*. Что и требовалось доказать.

Теорема 2. Собственные функции самосопряжѐнного оператора ˆ ,

принадлежащие разным собственным значениям – ортогональны, то есть:

fm* (x) fn (x)dx 0,

если am ≠ an.

Доказательство. Пусть:

ˆ	x an fn	x и	ˆ	x am fm x .
Afn			Afm

(15)

(*)

Перепишем (*):

*	ˆ			*	ˆ				*
dxfm	x Afn	(x) an fn (x) fm (x) Afn (x)dx an							fm	(x) fn (x)dx ,
	ˆ *	*	* *		ˆ *	*			*		*
dxfn x A fm			(x) am fm	(x) fn (x) A fm			(x)dx am				fn (x) fm (x)dx ,
*	ˆ			ˆ *		*		*
fm (x) Afn (x)dx fn (x) Afm (x)dx					(an am )			fm (x) fn (x)dx .
Левая	часть	последнего		равенства	есть	0	в	силу	самосопряжѐнности
	ˆ					*	an am 0
оператора A , а справа – из неравенства					an am		an am 0				, следует:

fm* x fn x dx 0,

что и требовалось доказать.

При m = n интеграл (15) не равен нулю, но должен быть конечным, так как именно такие функции будут рассматриваться в квантовой механике (квадратично-интегрируемые). Пусть:

fn* (x) fn (x)dx Cn2 ,

так как интеграл положителен. Рассмотрим функции:

ψn (x)	1	fn (x) ,	(*)

	Cn

которые также будут собственными функциями оператора			ˆ
			A при тех же
собственных значениях (см. замечание), тогда:
	n x	2 dx 1 .	(16а)

Объединяя это условие с (15), получим:
m* x n x dx δmn ,			(16б)

где δmn – символ Кронекера.

Определение 9. Функции, удовлетворяющие условию (16б), называются

ортонормированными, а числа Cn – коэффициентами нормировки.

В случае непрерывного спектра собственных значений оператора, ортогональность функций, принадлежащих разным собственным значениям a

и a´, должна была бы записываться в виде:				fa* x fa x dx 0, a a .
	fa* x fa	x dx 0,	a a ;

Выполнение обоих условий возможно, но функции fa(x), при этом, не могут быть квадратично - интегрируемы, то есть:

fa x 2 dx ,

атакие функции нормировать нельзя. Эта трудность обходится с помощью использования δ-функции Дирака, которая определяется следующим образом:

0,	a a
δ a a	a a	.	(17)
,	a a

С еѐ помощью ортогональность и нормировку функций непрерывного
спектра можно записать в форме:
fa* x fa x dx (a a ) .			(18)

Назвать δ-функцию функцией можно только с большой натяжкой, так как эта функция относится к классу обобщѐнных. Остановимся на еѐ

свойствах, используемых далее:		δ z δ z ,
		δ z δ z ,								(Д1)

	f z	δ z z0 dz f z0 ,								(Д2)
		f z0		, z0 a, b
b

f z δ z z0 dz			0, z0 a, b						,	(Д3)
a			0, z0 a, b
	δ z C f z dz		n		δ z		-zk	f z dz ,
					δ z		-zk			(Д4)
										(Д4)
			k 1
						z	z zk
							z zk

где zk – корни уравнения:

z C 0 ,

а C – число (константа), которое может быть и ноль.

Если в уравнении (11) у разных собственных функций оператора ˆ

собственные значения одинаковые, то такие функции не обязаны быть ортогональными (см. Теорему 2), что не позволяет использовать свойства ортонормируемости всех собственных функций оператора, так необходимого в дальнейшем.

Определение 10. Если в уравнении:

ˆ	x an	fn x ,
Afn

начиная с n = p + 1, (p – натуральное число)

ap 1 ap 2 ap k ,

то, соответствующие им разные функции fp+1, fp+2, …, fp+k называются

вырожденными, а целое число k называется кратностью вырождения.

Теорема 3. Если в уравнении:

ˆ	x an	fn x ,
Afn
ˆ		оператор, имеет место k-кратное
где A – линейный самосопряжѐнный

вырождение (при ap+1), то линейная комбинация из k-вырожденных различных функций будет собственной функцией этого оператора с тем же собственным значением.

Доказательство: рассмотрим случай k = 2, то есть ap+1 = ap+2 = a, тогда

ˆ	x a f p 1 x ,	ˆ	x a f p 2 x
Af p 1		Af p 2

Покажем, что линейная комбинация f = C1fp+1 + произвольные постоянные, удовлетворяет условию:

		ˆ	af ;
		Af	af ;	a C1 f
ˆ	C2	ˆ	ˆ
A C1 f p 1	C2	f p 2 C1 Af p 1	C2 Af p 2

что и требовалось доказать.

C2fp+2, где C1 и C2 –

p 1 C2 f p 2 ,


Следствие. Из разных вырожденных функций			fp+i ( i 1, k ) с помощью

надлежащего выбора констант Ci ( i 1, k )			можно построить k-

линейнонезависимых функций, которые будут ортогональны между собой. В

итоге, все собственные функции оператора ˆ , включая и вырожденные,

можно, в принципе, сделать ортогональными.

Теорема 4. Для того, чтобы два линейных оператора ˆ и ˆ имели общую

A B

систему собственных функций необходимо и достаточно, чтобы они коммутировали.

Необходимость:		пусть,		{Ψn}	–	общая	система	собственных функций
ˆ	ˆ
операторов A и	B :
ˆ		ˆ				ˆ ˆ	ˆ	bn an n ,
A		B n	bn n A B n				Abn n	bn an n ,
ˆ		ˆ	an n			ˆ ˆ	ˆ	anbn n .
B		A n	an n		B A n		Ban n	anbn n .
Вычтем из верхнего уравнения нижнее:
		ˆ	ˆ	ˆ	ˆ	bn an	anbn n 0 ,
		AB n BA n				bn an	anbn n 0 ,

ˆ ˆ	ˆ ˆ	0 , что и требовалось доказать.
то есть (AB BA) n		0 , что и требовалось доказать.
Достаточность: пусть
		A, B 0 ,
а { n } –	собственные функции			одного	ˆ
а { n } –	собственные функции			одного	из операторов, например, A :
ˆ					ˆ
A n an n	. Подействуем на это равенство оператором B :
		ˆ ˆ		ˆ ˆ	ˆ
		B A n an n		BA n	an B n .
		ˆ ˆ	ˆ	ˆ
Используя условие теоремы AB BA , получим:
		ˆ	ˆ	ˆ	,
		A B n		an B n	,
то есть n	ˆ				ˆ
то есть n	и B n	– собственные функции оператора A , принадлежащие

одному собственному значению an. Значит, они могут различаться между собой только на константу, которую назовѐм bn и:

B n bn n ,

что доказывает наше утверждение.

Полнота системы собственных функций операторов

Теорема 5. Система собственных функций {fn} операторного уравнения:

ˆ	(x) an	fn (x)	(11)*
Afn

полна; это значит, что любую функцию Ψ(x), определяемую в той же области переменных x, можно представить в виде:

x Cn fn x ,	(19)
n
где Cn – числа коэффициенты разложения.
Если спектр собственных значений непрерывен:
ˆ	(11)
Afa (x) afa (x) ,	(11)
то:
x Ca fa x da ,	(20)

где интегрирование ведѐтся по всем возможным непрерывным собственным значениям a в уравнении (11), а Ca – функции непрерывной переменной a, записанные в форме коэффициентов разложения.

Доказательство: правильность разложений (19), (20) будет доказана, если мы найдѐм коэффициенты этих разложений через заданные функции Ψ(x) и f(x).

Умножим равенство (19) на f*k(x) и проинтегрируем по всем

непрерывным x:
fk* x x dx Cn fk* x fn x dx Cn δkn			Ck . (21)
	n	n
Умножим равенство (20) на	f * x	и проинтегрируем по x:
	a

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.12.2019570.37 Кб03044_sp_matem_kod_20.doc
#
21.09.2019157.7 Кб43095_bilet_2012.doc
#
08.12.2019450.56 Кб0312_9_tarih.doc
#
21.02.2016189.25 Кб49324-334.docx
#
21.02.2016112.18 Кб15350-360.docx
#
21.02.20161.38 Mб213lk_0.pdf
#
18.11.201927.84 Кб44 тема Айбек,Тенелбек.docx
#
21.02.201683.46 Кб144.Теория удара.doc
#
21.02.201627.99 Кб4640 самых лучших книг по саморазвитию.docx
#
21.02.2016779.11 Кб104069.docx
#
21.02.20161.03 Mб1206417_teploraschet201.doc