
- •Краткий конспект лекций
- •Транспонирование матрицы
- •Квадратная матрица
- •Определитель квадратной матрицы
- •Минор и алгебраическое дополнение
- •;. Свойства определителей
- •Практическое правило вычисление определителей
- •Обратная матрица
- •Ранг матрицы
- •Базисный минор матрицы
- •Эквивалентность матриц
- •Тема 1.2. Системы линейных алгебраических уравнений (слау)
- •Правило Крамера
- •Матричный метод
- •Метод Гаусса
- •Тема 1.3. Общее исследование систем линейных алгебраических уравнений
- •Теорема Кронекера‑ Капелли. Система линейных алгебраических уравнений (1.4) совместная тогда и только тогда, когда ранг матрицы коэффициентов систем уравнений равняется рангу расширенной матрицы: .
- •Определение 1.19. Рангом совместной системы линейных алгебраических уравнений называется ранг ее матрицы .
Тема 1.2. Системы линейных алгебраических уравнений (слау)
Система mлинейных алгебраических уравнений сnнеизвестными имеет вид:
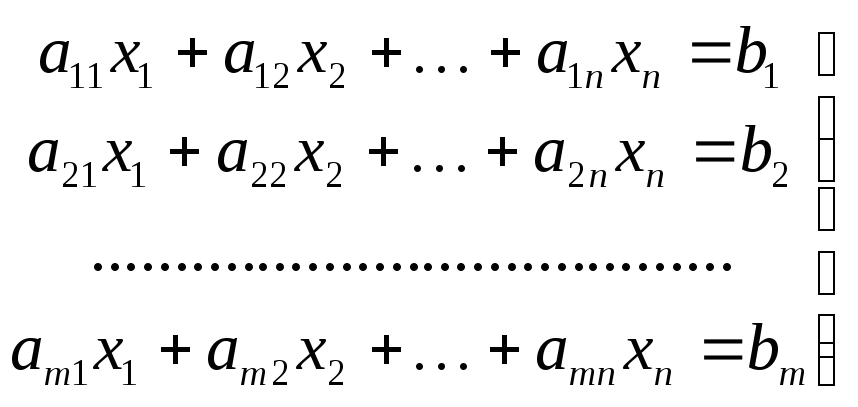 (1.2)
(1.2)
Совокупность чисел
![]() ,
которые, будучи подставленными в систему
(1.2) вместо неизвестных, обращают все
уравнения СЛАУ в числовые тождества,
называетсярешением системы.
,
которые, будучи подставленными в систему
(1.2) вместо неизвестных, обращают все
уравнения СЛАУ в числовые тождества,
называетсярешением системы.
Если система (1.2) имеет хотя бы одно решение, она называется совместной, в противном случае –несовместной.
Совместная система может обладать либо единственным решением, либо бесчисленным множеством решений.
Пусть А - матрица коэффициентов системы,
![]() - вектор- столбец неизвестных,
- вектор- столбец неизвестных,![]() -
вектор-столбец свободных членов. Тогда
в матричном виде система запишется в
виде
-
вектор-столбец свободных членов. Тогда
в матричном виде система запишется в
виде
![]()
Если количество уравнений m равно
количеству неизвестных n, система имеет
квадратную матрицу А порядка n. Определитель
![]() называетсяопределителем системы.
называетсяопределителем системы.
Правило Крамера
Теорема 1.6.Если определитель системы![]() отличен от нуля (т. е. r(A) = n), то система
совместна и имеет единственное решение,
которое определяется по формулам:
отличен от нуля (т. е. r(A) = n), то система
совместна и имеет единственное решение,
которое определяется по формулам:
![]() ( j = 1, 2, ..., n ), (1.3)
( j = 1, 2, ..., n ), (1.3)
где
![]() есть определитель, полученный из
определителя системы
есть определитель, полученный из
определителя системы![]() заменой j-го столбца столбцом свободных
членов. Формулы (1.3) называютсяформулами
Крамера.
заменой j-го столбца столбцом свободных
членов. Формулы (1.3) называютсяформулами
Крамера.
Доказательство
Поскольку
![]() ,
матрица А коэффициентов системы
невырожденная и имеет обратную матрицу
А-1, причем А-1 является
единственной.
,
матрица А коэффициентов системы
невырожденная и имеет обратную матрицу
А-1, причем А-1 является
единственной.
Умножим левую и правую части системы АX = B на А-1
слева. Получим А-1АX = А-1-B, откуда EX= А-1B и, окончательно,
X= А-1B (1.4)
Решение (1.4) – единственное решение СЛАУ в силу единственности существования обратной матрицы.
Запишем равенство (1.4) в координатной форме:
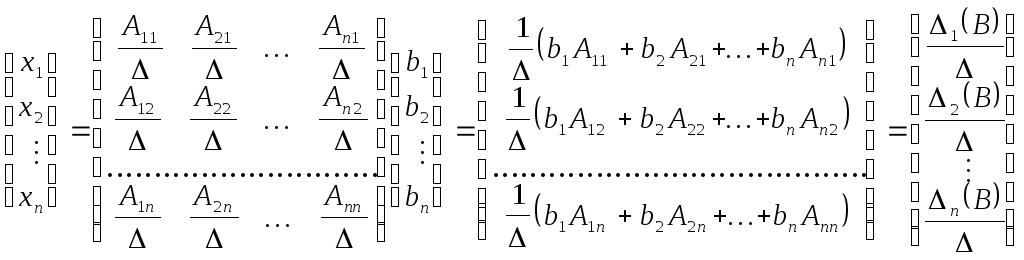
Выражение b1A1j + b2A2j+ ...+ bnAnjесть разложение
определителя![]() по элементам j-го столбца (теорема
Лапласа).
по элементам j-го столбца (теорема
Лапласа).
Таким образом,
![]() (j = 1, 2, ..., n).
(j = 1, 2, ..., n).
Задача 1.6. Решить СЛАУ

Решение
Найдем определитель системы
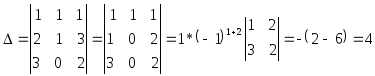
![]() ,
следовательно, система совместна и
имеет единственное решение, которое
может быть найдено по формулам Крамера.
Вычислим вспомогательные определители:
,
следовательно, система совместна и
имеет единственное решение, которое
может быть найдено по формулам Крамера.
Вычислим вспомогательные определители:
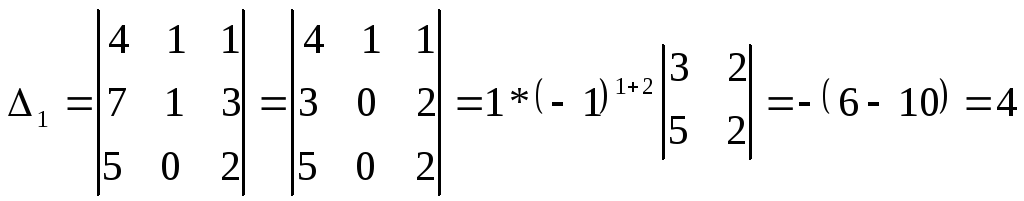

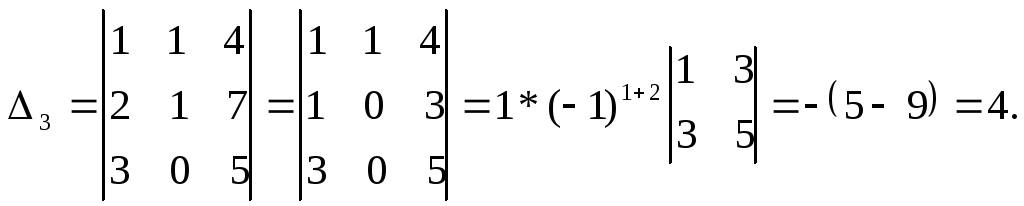
![]()
Тогда решение СЛАУ
![]() ;
;
![]() ;
;![]()
![]()
Матричный метод
Для систем с невырожденной квадратной матрицей коэффициентов системы довольно часто используют матричный метод.
Итак, пусть система уравнений заданная своей матричной формой записи:
![]() .
.
В соответствии с условием задачи матрица есть невырожденной, тогда у нее существует обратная матрица , причем такая матрица будет единственной.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Последнее соотношение задает матричную форму решения систем линейных алгебраических уравнений размерностей с невырожденной матрицей коэффициентов .
Задача 1.7.Найти решение СЛАУ матричным методом
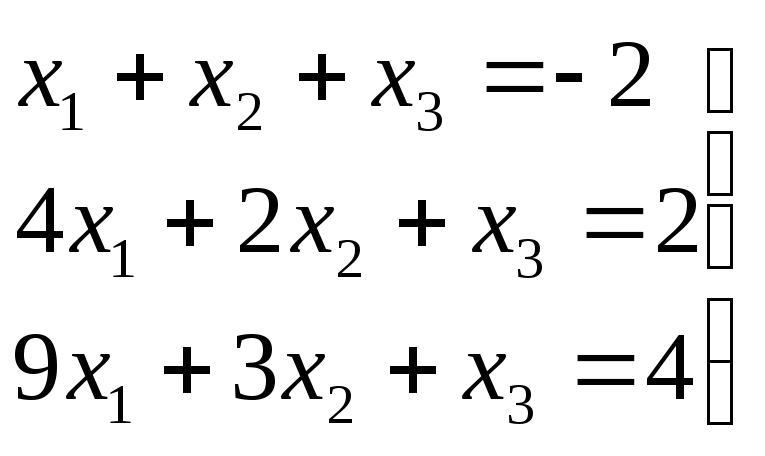
Решение
Вычислим определитель матрицы коэффициентов системы

![]()
Поскольку
![]() ,
то исходная система имеет единственное
решение.
,
то исходная система имеет единственное
решение.
На
следующем этапе необходимо найти
обратную матрицу
![]() к матрице коэффициентов системыA.
к матрице коэффициентов системыA.
Для этого найдем соответствующие алгебраические дополнения.
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Присоединенная матрица будет иметь вид
 .
.
Обратная матрица определяется таким образом:
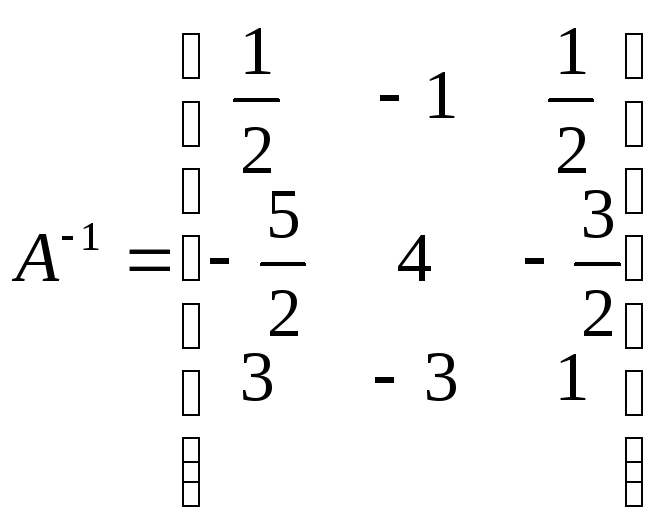 .
.
Непосредственно решение исходной системы найдем из соотношения:
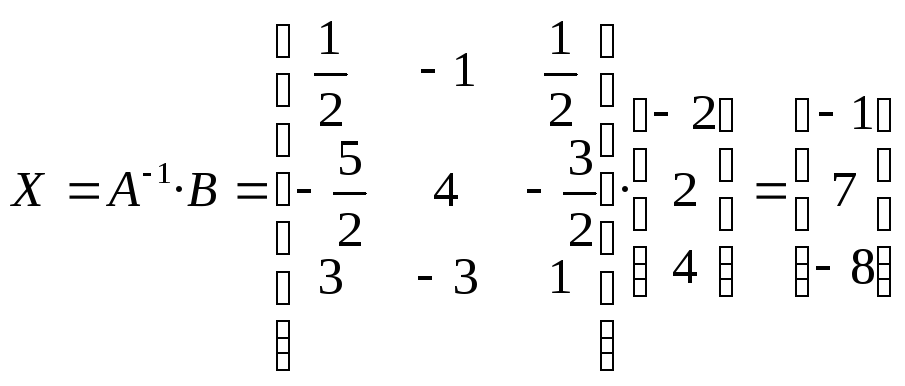 .
.
Итак,
![]()
![]() ,
,![]() .
.
Проверка:

СЛАУ решена верно.
