
- •Краткий конспект лекций
- •Транспонирование матрицы
- •Квадратная матрица
- •Определитель квадратной матрицы
- •Минор и алгебраическое дополнение
- •;. Свойства определителей
- •Практическое правило вычисление определителей
- •Обратная матрица
- •Ранг матрицы
- •Базисный минор матрицы
- •Эквивалентность матриц
- •Тема 1.2. Системы линейных алгебраических уравнений (слау)
- •Правило Крамера
- •Матричный метод
- •Метод Гаусса
- •Тема 1.3. Общее исследование систем линейных алгебраических уравнений
- •Теорема Кронекера‑ Капелли. Система линейных алгебраических уравнений (1.4) совместная тогда и только тогда, когда ранг матрицы коэффициентов систем уравнений равняется рангу расширенной матрицы: .
- •Определение 1.19. Рангом совместной системы линейных алгебраических уравнений называется ранг ее матрицы .
Практическое правило вычисление определителей
При вычислении определителей широко используются формулы разложения по строке или столбцу (теорема Лапласа), а также свойство, позволяющее, не изменяя величины определителя, преобразовать его к такому виду, когда какой-либо ряд содержит максимально возможное число нулей. Именно этот ряд рационально принять в качестве ряда для разложения по Лапласу. Такой подход к вычислению определителей называется правилом понижения порядка.
Задача 1.2.Вычислить определитель

В качестве ряда для разложения рационально использовать вторую строку, которая содержит два нулевых элемента. Для уменьшения объема последующих вычислений можно добиться большего числа нулей в этой строке. Работать будем со столбцами. Сложим соответствующие элементы второго и третьего столбцов и запишем результат на месте третьего столбца.
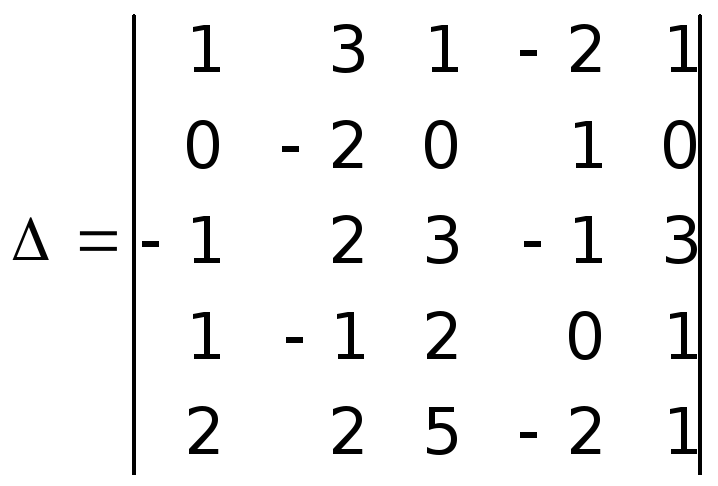
Используя свойство 8, добавим к элементам второго столбца соответствующие элементы четвертого столбца, умноженные на число 2. Получим

Далее разложим определитель по элементам второй строки.
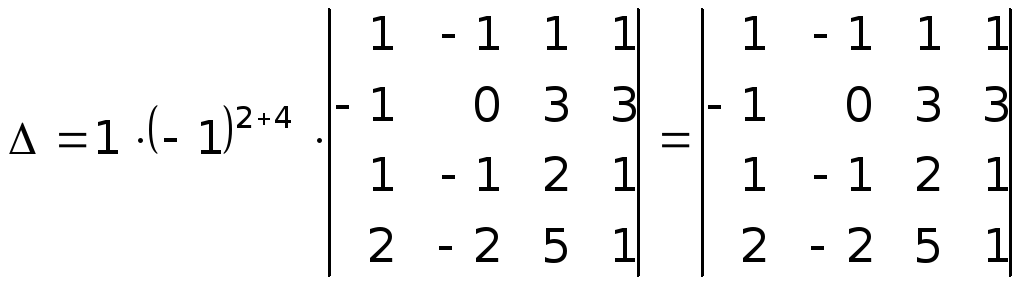 .
.
Теперь
в определителе четвертого порядка
добьемся наибольшего числа нулей в
третьей строке. Для этого умножим на
![]() элементы первой строки и сложим их с
соответствующими элементами третьей
строки.
элементы первой строки и сложим их с
соответствующими элементами третьей
строки.
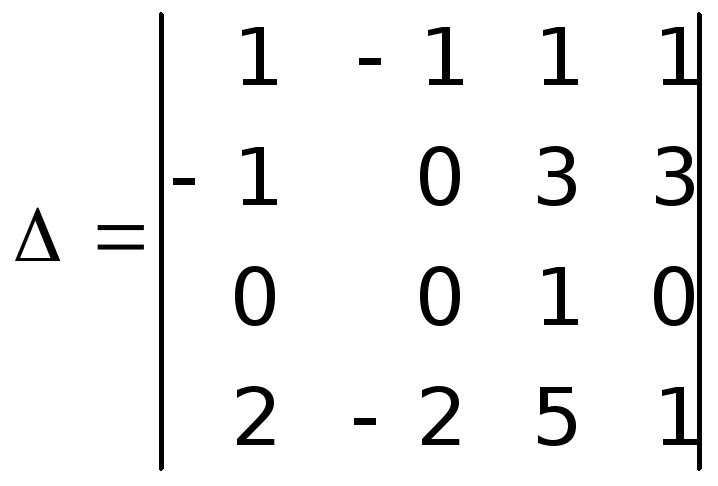 .
.
Разложим определитель четвертого порядка по элементам третьей строки
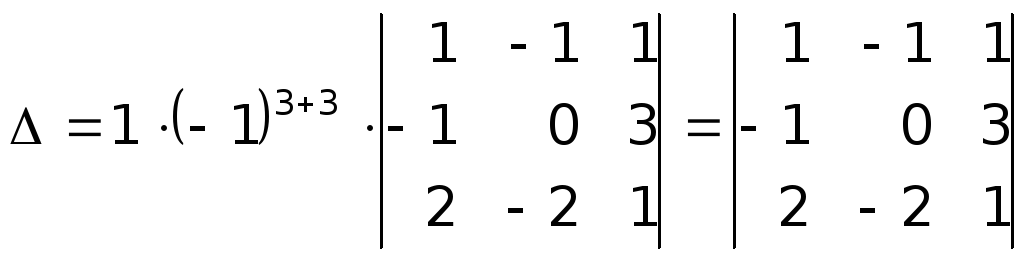 .
.
В
определителе третьего порядка добьемся
наибольшего числа нулей во втором
столбце. Будем работать со строками.
Все элементы первой строки умножим на
число
![]() и сложим с соответствующими элементами
третьей строки
и сложим с соответствующими элементами
третьей строки
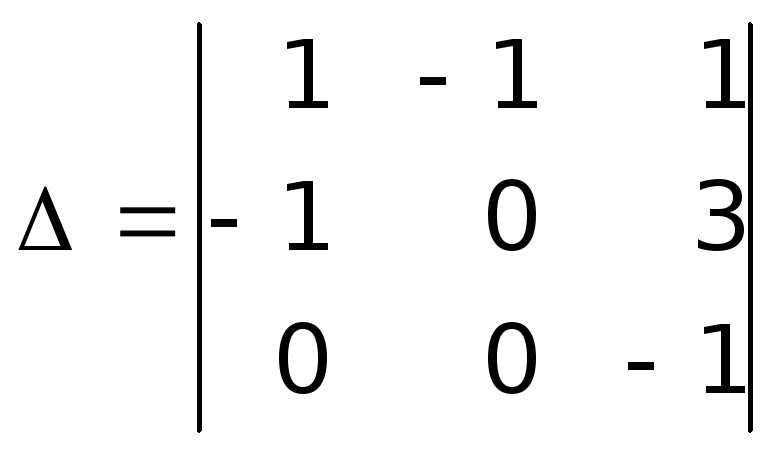 .
.
Применим теорему Лапласа, выбрав в качестве ряда для разложения второй столбец. Получим:
![]() .
.
Наконец, вычисляя определитель второго порядка, окончательно имеем
![]()
Обратная матрица
Одно
из важнейших свойств умножения чисел
состоит в том, что для каждого числа
![]() ,
отличного от нуля, существует обратное
,
отличного от нуля, существует обратное![]() такое, что
такое, что
![]() .
.
Оказывается,
что нечто подобное имеет место и для
матриц, причем роль условия
![]() играет условие, состоящее в том, что
определитель матрицы
играет условие, состоящее в том, что
определитель матрицы![]() отличен от нуля.
отличен от нуля.
Определение
1.13.Квадратная матрица называетсяневырожденной, если ее определитель
не равен нулю![]() .
В противном случае
.
В противном случае![]() матрица называетсявырожденной.
матрица называетсявырожденной.
Определение
1.14.Матрица![]() называется обратной по отношению к
матрице
называется обратной по отношению к
матрице![]() ,
если выполняется соотношение:
,
если выполняется соотношение:
![]() .
.
Условие существования обратной матрицы сформулируем в виде теоремы.
Теорема
1.1.Для того, чтобы квадратная матрица![]() имела обратную, необходимо и достаточно,
чтобы она была невырожденной.
имела обратную, необходимо и достаточно,
чтобы она была невырожденной.
Обратная матрица находится по следующей схеме:
1.
Вычисляется определитель
![]() исходной квадратной матрицы
исходной квадратной матрицы![]() -го
порядка.
-го
порядка.
2.
Формируется матрица, составленная из
алгебраических дополнений элементов
![]() исходной квадратной матрицы
исходной квадратной матрицы![]() .
Такая матрица называетсясоюзной по
отношению к матрице
.
Такая матрица называетсясоюзной по
отношению к матрице![]() и обозначается
и обозначается![]() :
:
 .
.
3.
Транспонируют союзную матрицу, определяя
тем самым так называемую присоединенную
матрицу. Такая матрица обозначается![]() и выглядит следующим образом:
и выглядит следующим образом:
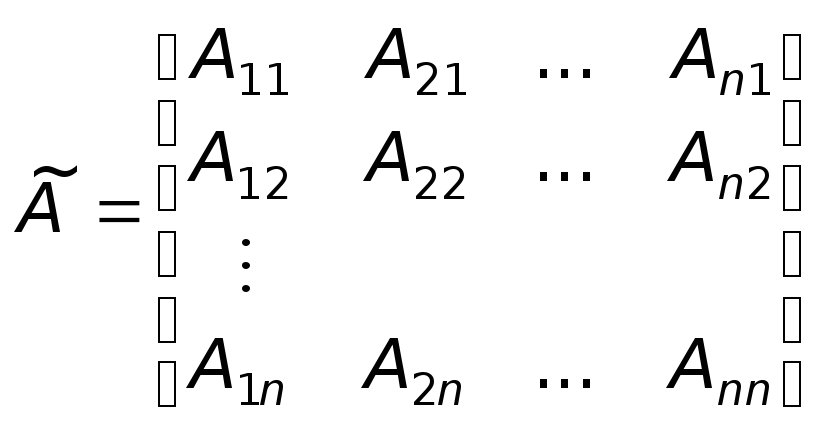 .
.
4.
Обратная матрица
![]() по отношению к матрице
по отношению к матрице![]() находится по формуле:
находится по формуле:
![]() .
.
Задача
1.3.Дана матрица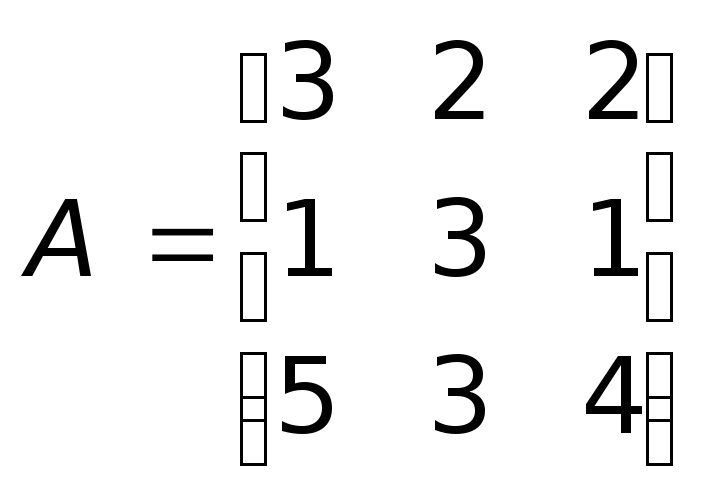 .
Найти обратную матрицу по отношению к
заданной.
.
Найти обратную матрицу по отношению к
заданной.
Вычислим
определитель матрицы
![]() .
.
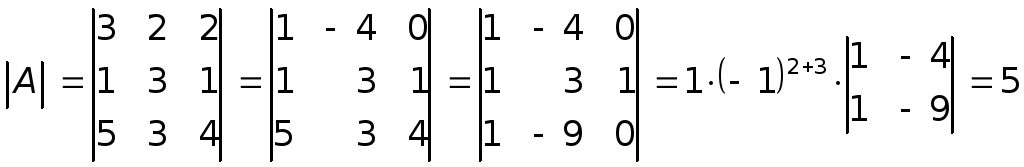 .
.
Матрица невырождена, следовательно, обратная матрица существует.
Найдем алгебраические дополнения элементов определителя.
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Формируем союзную матрицу
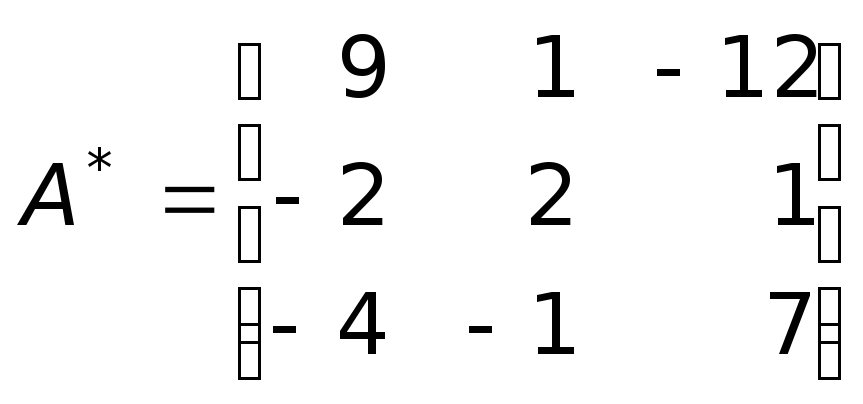 .
.
Определим присоединенную матрицу
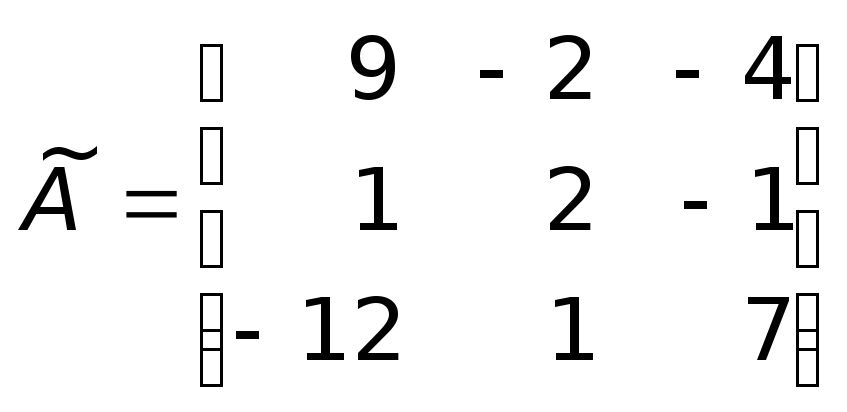 .
.
Найдем
обратную матрицу
![]() по отношению к матрице
по отношению к матрице![]() :
:
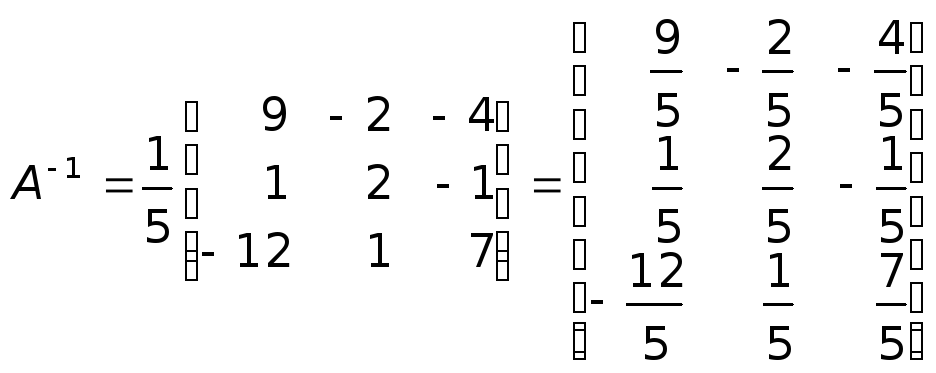 .
.
