І ітерація

Вибираємо точку, що належить множині допустимих планів задачі. Розглянемо, наприклад, точку .

Визначимо градієнт цільової функції:

.

В точці обчислюємо значення градієнта:

.

Використовуючи розраховане значення градієнта, записуємо і вводимо нову цільову функцію: . Маємо таку задачу лінійного програмування:

.

Розв’язуючи цю задачу симплексним методом, знаходимо її оптимальний план: .

Знайдемо новий допустимий план задачі, використовуючи формулу для визначення координат наступної точки.

Визначаємо координати точки Х₁:

, ,

Знайдемо крок такий, за якого досягається максимальне значення цільової функції. Для цього підставимо розраховані значення для х₁, х₂, які виражені через , у цільову функцію :

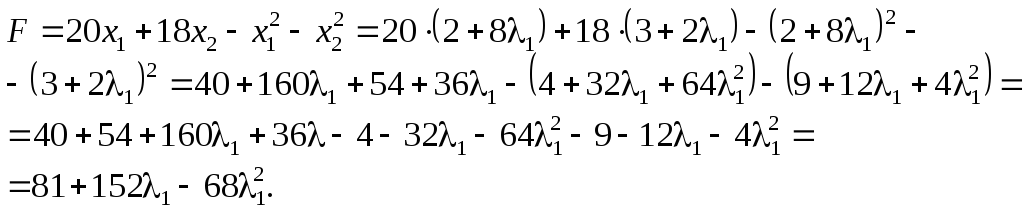
Отримали функцію, що залежить від . Знайдемо значення , за якого функція досягає максимуму, тобто коли її похідна дорівнює нулю:

Оскільки , то беремо . Тоді наступна точка Х₁ має координати:

.

Для знайденої точки обчислюємо значення цільової функції: .

Іі ітерація

Узявши точку , обчислюємо значення градієнта в ній:

Використовуючи розраховане значення градієнта, вводимо нову цільову функцію: . Отримуємо таку задачу лінійного програмування:

.

Розв’язавши її симплексним методом, отримуємо оптимальний план: .

За формулою визначаємо координати наступної точки наближення.

Визначаємо координати точки Х₂:

,

.

Знайдемо такий крок λ₂, за якого досягається максимальне значення цільової функції:

Матимемо .

Обчислимо координати наступної точки Х₂:

Для знайденої точки значення цільової функ­ції дорівнює: .

Продовжуючи процес у аналогічний спосіб, на ІІІ ітерації визначаємо точку і переконуємося, що значення цільової функції знову зростає: .

На IV ітерації розраховуються координати точки , для якої .

V ітерація

Узявши точку , обчислюємо значення градієнта в ній:

.

Використовуючи значення цього вектора (градієнта), вводимо нову цільову функцію: і маємо таку задачу лінійного програмування:

,

.

Розв’язавши цю задачу, отримаємо значення оптимального плану , тобто повертаємося до попереднього значення. Отже, точку з координатами вважаємо оптимальним планом, оскільки маємо нульовий градієнт функції, тобто цей план поліпшити вже не можна.

Заключні зауваження

Задачі нелінійного програмування часто виникають як в теорії управління, так і в інших науках, і їх систематичне дослідження, що почалося в кінці 40-х років, привело до виникнення самостійної наукової дисципліни — нелінійного програмування.

У рамках вищеописаного розділу сформульовані лише основні теоретичні засади та найбільш вивчені методи розв’язування задач нелінійного програмування.

Оскільки для задач нелінійного програмування не існує універсального методу їх розв’язання, то не всі наведені методи однаково зручні для розв’язування певної практичної задачі. В кожному конкретному випадку необхідно вибирати кращий метод. Не можна в рамках даного посібника викласти всі відомі нині методи нелінійного програмування, тому залишилися поза увагою деякі цікаві методи. Бажаючим детальніше вивчити нелінійне програ­мування, доцільно ознайомитися з літературою [13, 19, 20, 28].

Головною метою розгляду даної теми було звернення уваги майбутніх фахівців-економістів на практичне значення використання моделей нелінійного програмування. У більш узагальнених постановках економічних задач визначення точного виду функцій у математичній моделі може видатися неможливим, однак за конкретних умов точний вигляд функцій часто визначається безпосередньо. Тоді розв’язок на основі побудованої моделі дає оптимальний план, адаптований до реальних умов.

Контрольні запитання

1. Як записується в загальному вигляді задача нелінійного програмування?

2. Труднощі розв’язування задач нелінійного програмування.

3. Функція Лагранжа.

4. Метод Лагранжа.

5. Яка функція називається опуклою (угнутою)?

6. Сформулюйте необхідні та достатні умови існування сідлової точки для деякої диференційовної функції.

7. Теорема Куна—Таккера.

8. Сформулюйте задачу квадратичного програмування.

9. Назвіть етапи розв’язування задачі нелінійного програмування методом кусково-лінійної апроксимації.

Приклади та завдання для самостійної роботи

Задача 8.1. Використовуючи метод Лагранжа, знайдіть точку умовного екстремуму.

1) , 2) ,

. .

Задача 8.2. На виробництво трьох видів продукції (A; B; C) використовують матеріальні, трудові та фінансові ресурси. Норми витрат цих ресурсів на одиницю продукції, їх запаси, а також фор­мули визначення прибутку від реалізації одиниці продукції, що залежать від обсягів виробництва, наведено в табл. 8.3.

Таблиця 8.3

Вид ресурсу, показник	Продукція			Запас ресурсу
	А	В	С
Матеріальні	4	5	7	100
Трудові	3	6	8	120
Фінансові	2	1	4	75
Прибуток				—
Обсяг виробництва				—

Передбачаючи, що попит на продукцію видів В і С відомий і становить 12 і 8 од., а ресурси необхідно використати повністю, визначте оптимальний план виробництва продукції кожного виду. Розрахуйте оцінки ресурсів і здійсніть економічний аналіз оптимального плану.

103