
OM-labi-1
.pdf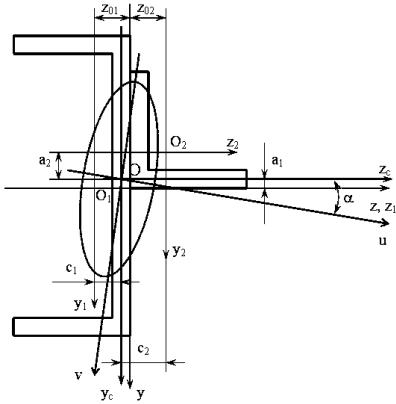
де y1 =0 , z1 =0 – координати центру ваги першої фігури;
y2 =−z02 =−2,19 см, z2 =z01 +z02 =1,94+2,19=4,13 см – координати центру ваги другої фігури.
Визначаємо центральні моменти інерції перерізу відносно осей Оyс , Оzс:
I |
z |
|
=I |
z |
+a 2 A +I |
z |
+a |
2 A = |
|
|||
|
c |
|
|
1 |
1 |
2 |
2 |
2 |
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
=1090+0,682 20,7+67+1,512 9,38=1178 см4, |
||||
де |
a1 =y1 −yc =0−(−0,68)=0,68 |
см; a2 =y2 −yc =−2,19−(−0,68)=−1,51 см – |
||||||||||
відстані між осями zс |
і z1, z2 відповідно. |
|||||||||||
|
|
|
Iy |
c |
=Iy |
+c12 A1 +Iy |
+c22 A2 =86+1,292 20,7+57+2,842 9,38=253 см4, |
|||||
|
|
|
|
|
1 |
|
|
|
|
z |
|
|
де с1 =z1 −zc =0−1,29=−1,29 см; |
c2 =z2 −zc =4,13−1,29=2,84 см – відстані між |
|||||||||||
осями yc і y1 , y2 відповідно.
Визначаємо відцентровий момент інерції перерізу відносно осей Оyс , Оzс
Izc yc =Iz1y1 +a1c1A1 +Iz2 y2 +a2c2 A2 =
=0−1,29 0,68 20,7+33,45−1,51 2,84 9,38=−24,9 см4.
Положення головних центральних осей інерції перерізу
|
2Izc yc |
|
2 (−24,9) |
|
′ |
|
tg2α= |
|
= |
|
|
=−0,054 ; |
α=−1°33 . |
Izc −Iyc |
1178−253 |
|||||
Якщо кут від’ємний, то центральні осі слід повернути за годинниковою стрілкою.
Головні центральні осьові моменти інерції дорівнюють
21

Iu,v = |
Izc +Iyc |
± |
1 |
(Izc −Iyc )2 |
+4I Z2 Y = |
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
||||||||
|
|
2 |
|
=1178+253 |
±1 |
c c |
|
|
|
|
|
|||
|
|
|
|
|
(1178−253)2 +4 (−24,9)2 = |
|||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
=715,5± |
1 855625+4 620,01=715,5±1 |
855625+2480,04 = |
||||||||||||
|
|
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
||
|
|
|
|
|
=715,5±2 |
858102,04 =715,5±463,2 см . |
||||||||
|
|
Iu =715,5+463,17=1178,7 см4; |
Iv =715,5−463,17=252,3 см4. |
|||||||||||
Головні радіуси інерції: |
|
|
|
|
|
|
|
|||||||
|
|
i |
= |
|
Iu |
= |
1178 |
=6,3 см; |
i = |
Iv |
= |
253 |
=2,9 см. |
|
|
|
|
|
|
|
|
||||||||
|
|
u |
|
|
A |
30,08 |
|
|
v |
A |
30,08 |
|
||
|
|
|
|
|
|
|
|
|
||||||
У даному випадку головні моменти інерції не суттєво відрізняються від центральних моментів інерції відносно осей, які проведені паралельно основним розмірам.
Слід пам’ятати, що в розрахунках на міцність та жорсткість балки при їх згині у формулах використовують головні центральні моменти інерції.
Задача № 4
Розрахунок вала постійного перерізу на міцність та жорсткість при крученні
Вихідні дані:
схема – 2; довжини дільниць: a = 2, 2 м, b =1,5 м, |
c = 2,9 м, d =1,5 м; кру- |
тні моменти: T1 =1, 2 кН·м, T2 =1, 2 кН·м, T3 = 0,8 |
кН·м; допустиме напру- |
ження [τ]= 4 кН/см2 ; модуль пружності при зсуві G =8 104 МПа. |
|
Розв’язання: |
|
1. Визначимо величину крутного моменту T , при якому кут повороту в перерізі 4 на вільному кінці стержня дорівнюватиме ϕ4 = 0 .
Він визначається, як сума кутів закручування на кожній ділянці:
ϕ4 = ϕ0 +ϕ0−1 +ϕ1−2 +ϕ2−3 +ϕ3−4 = 0 .
Запишемо вирази кутів закручування для кожної ділянки, починаючи з вільного кінця.
22

Ділянка 3-4:
|
|
ϕ |
= |
Mкр3−4 d |
; M |
3−4 |
=T ; |
ϕ |
|
= |
T d |
. |
||||||||
|
|
|
|
|
|
|
кр |
|
|
|||||||||||
|
|
3−4 |
|
|
G |
Iρ |
|
|
|
|
|
3−4 |
|
G I ρ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ділянка 2-3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ϕ |
2−3 |
= |
Mкр2−3 c |
; M |
3−4 |
=T −T ; ϕ |
2−3 |
|
= (T −T3 ) c . |
|||||||||||
|
|
кр |
|
|||||||||||||||||
|
|
|
G Iρ |
|
|
|
|
|
3 |
|
|
|
G Iρ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ділянка 1-2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
Μ1−2 |
b |
|
|
|
|
|
|
|
|
|
||
|
|
|
ϕ |
|
= |
|
|
кр |
|
|
; |
Μ |
1−2 =T |
−T +T ; |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1−2 |
|
|
|
G Iρ |
|
|
|
кр |
|
|
|
3 |
2 |
|
||
|
|
|
|
|
|
|
|
|
(T −T3 +T2 ) b |
|
|
|
|
|||||||
|
|
|
|
|
|
|
ϕ1−2 = |
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
G Iρ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23

Ділянка 0-1: |
|
|
|
|
|
||||
|
|
|
M |
0−1 a |
|
|
|
||
ϕ |
|
= |
|
кр |
|
; M 0−1 =T −T +T |
+T ; |
||
0−1 |
|
|
|
||||||
|
|
G Iρ |
|
кр |
3 2 |
1 |
|||
|
|
|
(T −T3 +T2 |
+T1 )a |
|
|
|||
|
|
|
ϕ0−1 = |
. |
|
||||
|
|
|
|
G Iρ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
ϕ0 = 0 – кут закручування в затисненні.
Отримані вирази кутів закручування для кожної ділянки підставимо у вираз для визначення ϕ4:
ϕ4 |
= |
(T −T3 +T2 +T1 ) a |
+ |
(T −T3 +T2 ) b |
+ |
(T −T3 ) c |
+ |
T d |
= 0 . |
||
G Iρ |
G |
Iρ |
G Iρ |
G Iρ |
|||||||
|
|
|
|
|
|
||||||
На підставі принципу суперпозиції та закону Гука одержуємо:
T(a +b +c +d )−T3 (a +b +c)+T2 (a +b)+T1 a = 0;
Т8,1−Т3 6,6 +Т2 3,7 +Т1 2, 2 = 0;
Т = 0,8 6,6 −1, 2 3,7 −1, 2 2, 2 = −0, 222 кН·м. 8,1
2. Побудуємо епюру крутних моментів.
Користуючись методом перерізів, визначимо крутні моменти на відповідних ділянках вала:
|
0 ≤ x |
|
≤1,5 |
м; |
|
|
M 3−4 |
=Т = −0,222 кН·м; |
||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
кр |
|
|
|
|
|
||||
|
0 ≤ x ≤ 2,9 |
м; |
|
M 2−3 =Т −Т |
3 |
|
= −0,222 −0,8 = −1,022 кН·м; |
|||||||||||||
|
3 |
|
|
|
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 ≤ x ≤1,5 м; |
M |
1−2 =Т −Т |
3 |
|
+Т |
2 |
|
= −0,222 −0,8 +1,2 = 0,178 кН·м; |
||||||||||||
|
2 |
|
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 ≤ x |
≤ 2, 2 м; M 0−1 |
=Т −Т |
3 |
+Т |
2 |
+Т |
1 |
= −0,222 −0,8 +1,2 +1,2 =1,378 кН·м. |
||||||||||||
1 |
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Виконаємо підбір діаметра стержня. |
||||||||||||||||||||
Складемо умову міцності: |
|
Mкрmax |
|
|
|
|
|
|
Mкрmax |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
τmax |
= |
|
|
|
|
|
|
= |
|
≤[τ]. |
||||||
|
|
|
|
|
W |
|
|
|
0, 2D3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
Визначаємо необхідний діаметр стержня: |
||||||||||||||||||||
|
|
D ≥ 3 |
|
Mкрmax |
|
|
|
|
|
|
|
|
137,8 |
|
||||||
|
|
|
= |
3 |
|
0,2 4 =5,564 см. |
||||||||||||||
|
|
0,2 [τ] |
|
|||||||||||||||||
Приймаємо D = 6 см.
Полярний момент інерції перерізу:
24
Iρ = π32D4 = π3264 =127, 235 см4. 4. Побудуємо епюру кутів закручування.
Приймаємо, що кут закручування в затисненні дорівнює нулю. Далі визначаємо послідовно кути закручування для перерізів, у яких прикладені зовнішні
моменти Т1 , Т2 , Т3 |
та Т . Таким чином одержуємо ординати, на підставі яких |
|||||||||||||
будується епюра кутів закручування. |
|
|
|
|
|
|||||||||
Визначаємо кут закручування перерізу 1 на відстані a |
від лівого кінця |
|||||||||||||
стержня: |
|
|
|
|
|
|
Mкр0−1 |
а |
|
|
|
|
|
|
ϕ = ϕ |
0 |
+ϕ |
0−1 |
= 0 |
+ |
= |
137,8 220 |
= 29,78 |
10 |
−3 |
рад; |
|||
|
|
|
|
|||||||||||
1 |
|
|
|
G Iρ |
|
|
8 103 127, 235 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Визначаємо кут закручування перерізу 2 на відстані a +b від лівого кінця
стержня: |
|
|
|
|
17,8 150 |
|
ϕ |
2 |
= ϕ +ϕ |
= 29,78 10−3 + |
|
=32, 4 10−3 рад; |
|
|
|
|||||
|
1 1−2 |
|
8 |
103 127, 235 |
||
|
|
|
|
|||
Визначаємо кут закручування перерізу 3 на відстані a +b +c від лівого
кінця стержня: |
|
|
|
|
|
|
102, 2 290 |
|
ϕ = ϕ |
2 |
+ϕ |
2−3 |
=32, 4 10−3 |
− |
|
=3, 28 10−3 рад; |
|
|
|
|||||||
3 |
|
|
|
8 |
103 127, 235 |
|||
|
|
|
|
|
|
|||
Визначаємо кут закручування перерізу 4 на відстані a +b +c +d від лівого кінця стержня, тобто кут закручування вільного кінця стержня:
ϕ |
4 |
= ϕ +ϕ |
|
=3, 28 10−3 − |
|
|
22, 2 150 |
|
|
= 0 . |
||||
|
|
|
|
|
|
|
||||||||
|
3 |
3−4 |
|
|
|
8 103 127, 235 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
5. Визначимо найбільший відносний кут закручування: |
|
|||||||||||||
θ = |
|
Mкрmax |
= |
|
137,8 |
|
= |
0,133 10 |
−3 |
рад/см. |
||||
|
G Iρ |
8 |
103 127, 235 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Задача № 5 |
|
|
|
|
||||
|
Розрахунок балки на міцність при згині |
|||||||||||||
|
|
|
|
|
|
Вихідні дані: |
|
|
|
|
||||
консольна балка; схема 2; |
геометричні розміри: A=6 м; a1 =0,3A=1,8 м; |
|||||||||||||
a2 =0,3A=1,8 м; навантаження: M =9 кН·м; |
F =14 кН; |
q=10 кН/м; розрахун- |
||||||||||||
ковий опір R=1,6 кН/см2; співвідношення розмірів балки прямокутного перерізу h:b=1,5 .
За вказівкою викладача студенти можуть розрахувати одну із цих двох схем.
25

Розв’язання
Розв’язання задачі виконуємо відповідно до пп. 1-5 (с. 11).
Розрахункова схема
|
Епюри поперечних сил та згинальних моментів |
|||
Визначимо опорні реакції |
|
|
||
ΣmА =0 ; |
−МА −М −q 1,8 0,9+F 6=0; |
|||
|
МА =−9−10 1,8 0,9+14 6=58,8 кН·м; |
|||
ΣmВ=0 ; |
−МA −М −q1,8 5,1−RА6=0 ; |
|||
|
R = |
−58,8−9+10 1,8 5,1 |
=4 кН. |
|
|
|
|||
|
A |
6 |
|
|
|
|
|
|
|
Перевіримо правильність визначення опорних реакцій |
||||
ΣY =0 ; |
q 1,8−F −RA =0 ; 10 1,8−14−4=0 . |
|||
Побудуємо епюри внутрішніх зусиль.
У даному випадку слід розглянути дві ділянки.
Перша ділянка: 0≤x1 ≤1,8 м (ліворуч від проведеного перерізу)
Поперечні сили:
Q(x1)=RA −qx1; Q(0)=4 кН; Q(1,8)=4−10 1,8=−14 кН,
де qx1 – рівнодіюча сила від рівномірно розподіленого навантаження, яке
прикладене в центрі ваги.
Ордината нуля поперечної сили Q=0
RA −qx1 =0 ; x1 =RqA =104 =0,4 м.
26

Згинальні моменти
Mзг(x1)=M A +RAx1 −qx212 ;
Mзг(0)=58,8 кН·м;
Mmax (0,4)=58,8+4 0,8−10 0,42 2 =62 кН·м; Mзг(1,8)=58,8+4 1,8−10 1,82 2 =49,8 кН·м.
Друга ділянка: 0≤x2 ≤4,2 м (праворуч від проведеного перерізу) Поперечна сила Q(x2 )=−F =−14 кН; Згинальний момент Mзг(x2 )=Fx2 ;
Mзг(0)=0 ; Mзг(4,2)=14 4,2=58,8 кН·м.
Небезпечний переріз: M =58,8 кНм, Q=14 кНм.
Виконаємо підбір прямокутного перерізу. Момент опору згинанню
Wz =bh62 =b(1,56b)2 =0,375b3 .
Умова міцності
σmax =Mmax = Mmax3 ≤R .
Wz 0,375b
b≥3 |
Mmax |
|
5880кН см |
=21,4 |
см; |
|
|
=3 |
|
|
|||
0,375 R |
0,375 1,6кН/см2 |
|||||
|
h=1,5b=1,5 21,4=32,1 см. |
|
||||
Балка на двох опорах, R = 20 |
кН/см2. |
|
|
|||
Розрахункова схема
27
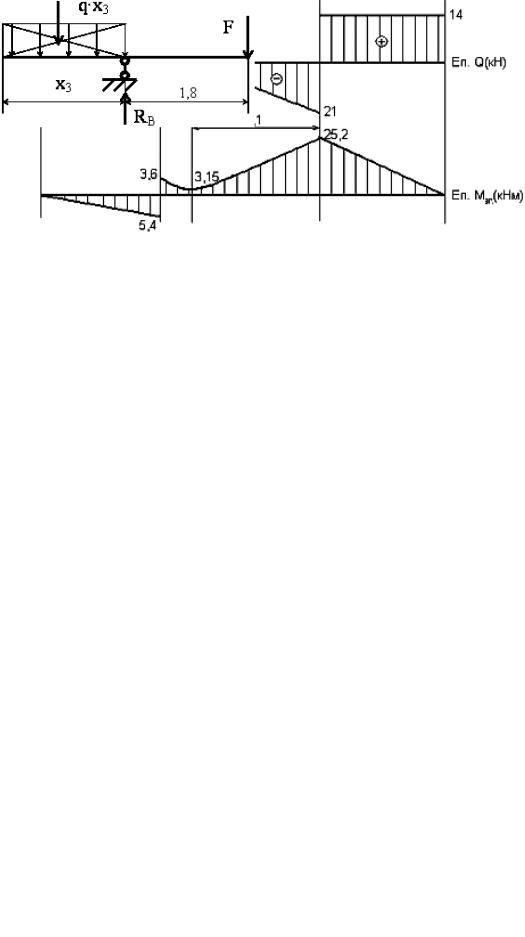
Епюри поперечних сил та згинальних моментів
Визначимо опорні реакції |
|
|
||
ΣmB =0 ; |
−RА4,2+М +q2,4 1,2−F1,8=0 ; |
|||
|
R = |
9+10 2,4 1,2−14 1,8 |
=3 кН; |
|
|
|
|||
|
A |
4,2 |
|
|
|
|
|
|
|
ΣmA =0 ; |
RB 4,2−F 6−q 2,4 3−M =0 ; |
|
|
R =−9+10 2,4 3+14 6 =35 кН. |
|
|
B |
4,2 |
|
|
|
Перевіримо правильність визначення опорних реакцій |
||
ΣY =0 ; |
|
q 2,4+F −RA −RB =0 ; |
|
|
10 2,4+14−3−35=0 . |
Побудуємо епюру внутрішніх зусиль. Розглянемо три ділянки:
Перша ділянка: 0≤x1 ≤1,8 м (ліворуч від проведеного перерізу)
Q(x1)=RA =3 кН;
Mзг(x1)=RA x1;
Mзг (0)=0 ; Mзг (1,8)=3 1,8=5,4 кН м.
Друга ділянка: 0≤x2 ≤1,8 м (праворуч від проведеного перерізу)
Q(x2 )=F =14 кН кН;
Mзг(x2 )=−Fx2 ;
Mзг(0)=0 ; Mзг(1,8)=−14 1,8=−25,2 кН·м.
Третя ділянка: 0≤x3 ≤2,4 м (праворуч від проведеного перерізу)
Q(x3)=F −RB +qx3 ,
де q x3 – рівнодіюча сила від рівномірно розподіленого навантаження, яке прикладене в центрі ваги.
28

Q(0)=14−35=−21 кН;
Q(2,4)=−2,1+10 2,4=3 кН.
Ордината нуля поперечної сили Q=0
F −RB +qx3 =0 ; x3 =−F q+RB =−1410+35 =2,1 м.
qx2
Mзг =−F(1,8+x3)+RBx3 − 23 ;
Mзг(0)=−14 1,8=−25,2 кН·м;
Mmax (2,1)=−14 3,9+35 2,1−10 22,12 =−3,15 кН·м; Mзг(2,4)=−14 4,2+35 2,4−10 2,42 2 =−3,6 кН·м.
Небезпечний переріз: M =25,2 кНм, Q=−21 кНм. |
|
|
||||||
Підбір двотавру |
|
|
|
|
|
|
||
σ |
max |
=Mmax ≤R ; |
W ≥ |
Mmax |
=2520 кН см |
=126 |
см3. |
|
|
||||||||
|
Wz |
A |
z |
RA |
20 кН/см2 |
|
|
|
|
|
|
|
|
|
|||
З таблиці |
сортаментів |
та |
ГОСТ обираємо двотавр |
№ 18, у якого |
||||
Wz =143 см3.
Враховуючи, що момент опору, необхідний за розрахунками (Wz =126 см3), більший від обраного, у даній системі буде невеликий запас міцності.
Задача № 6
Визначення переміщень при згині балок
Вихідні дані:
схема – 2; геометричні розміри: A=6 м; a=0,9 м, b=1,4 м, c=1,4 м; навантаження: F =6 кН, M =3 кН·м, q=3 кН/м; тип балки – двотавр № 24 ( IZ =3460 см4 =3460 10−8 м4); E =2 105 МПа = 2·108 кН/м2.
Потрібно:
Знайти прогин v та кут закручування θ в перерізі B .
29
Розв’язання:
Знайдемо опорні реакції
ΣmC =0 ; −RA 3,7+F 2,8+q 2,3 2,55+M =0 ;
RA =6 2,8+3 2,3 2,55+3 =10,11 кН; 3,7
ΣmA =0 ; |
RC 3,7+M −F 0,9−q 2,3 1,15=0 ; |
||
|
R = |
−3+6 0,9+3 2,3 1,15 |
=2,79 кН. |
|
|
||
|
C |
3,7 |
|
|
|
|
|
Перевіримо правильність визначення опорних реакцій
ΣY =0 ; q 2,3+F −RA −RC =0 ; 3 2,3+6−10,11−2,79=0 .
Скористуємося універсальним рівнянням зігнутої осі стержня, яке має вигляд
|
|
|
|
M |
|
x2 |
|
Q x3 |
qx4 |
|
q(x−2,3)4 |
|
F(x−0,9)3 |
|
|
υ(x)=v |
+θ |
0 |
x− |
|
0 |
|
− |
0 |
+ |
|
− |
|
+ |
|
. |
|
|
|
|
|
|
||||||||||
0 |
|
|
2!EI |
|
3!EI |
4!EI |
|
4!EI |
|
3!EI |
|
||||
|
|
|
|
|
|
|
|
||||||||
У цьому рівнянні: υ0 ; θ0 ; |
M0 ; Q0 – початкові параметри, які являють со- |
||||||||||||||
бою відповідно прогин, кут закручування, згинальний момент і поперечну силу на початку координат, інші складові – це ті величини, які залежать від
навантаження, що діє у прогоні балки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Граничні умови: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
при x=0 : |
|
υ0 =0 ; |
|
|
|
M0 =0 ; |
|
|
|
|
|
|
|
Q0 =10,11 кН; |
|
|
|
|
|
||||||||||||||
при x=3,7 : |
|
υ(3,7)=0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Після підстановки значень маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
υ(x)=θ0x− |
10,11x3 |
|
3x4 |
|
|
|
3(x−2,3)4 |
|
6(x−0,9)3 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
. |
|
|
|
|||||||||
|
3!EI |
4!EI |
|
|
4!EI |
|
3!EI |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Скористуємось умовою υ(3,7) і визначимо θ0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
θ0 3,7−10,11 3,73 |
+ |
3 3,74 |
− |
3 1,44 |
|
+ |
6 2,83 |
=0 ; |
|
|
|
|
|||||||||||||||||||
|
|
|
24EI |
24EI |
|
|
6EI |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
6EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
θ0 = |
40,45 |
=10,93 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
3,7EI |
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Підставимо θ0 у рівняння |
|
υ(x) |
|
і отримаємо універсальне рівняння для |
|||||||||||||||||||||||||||||
визначення прогинів у даній балці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
10,11x3 |
|
|
3x4 |
|
3(x−2,3)4 |
6(x−0,9)3 |
|
|||||||||||||||||||
υ(x)= |
|
|
10,93x− |
|
|
|
|
|
|
+ |
|
|
|
|
|
− |
|
|
|
|
|
|
+ |
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
EI |
|
|
|
|
|
3! |
|
|
|
|
|
|
4! |
|
|
|
|
4! |
|
|
|
|
|
|
3! |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Одержимо рівняння для визначення кутів закручування перерізів |
|||||||||||||||||||||||||||||||||
|
′ |
|
|
1 |
|
|
|
10,11x2 |
|
|
|
3x3 |
|
|
3(x−2,3)3 |
|
6(x−0,9)2 |
|
|||||||||||||||
θX =υ(x)= |
|
10,93− |
|
|
|
|
|
|
|
+ |
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
. |
|||||||
EI |
|
2! |
|
|
|
|
3! |
|
3! |
|
|
|
2! |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
