Розв’язання

1. Складемо вирази для згинальних моментів на ділянках та побудуємо епюру згинальних моментів (рис. 20):

І ділянка:

ІІ ділянка:

ІІІ ділянка:

ІV ділянка:

	Рис. 20. Епюра згинальних моментів
Рис. 21. Схема навантаження		Рис. 22. Епюра крутних моментів

Крутний момент буде виникати тільки на ІΙΙ та ІV ділянках:

ІІІ ділянка:

ІV ділянка:

Будуємо епюру крутних моментів (див. рис. 22).

2. Знайдемо розрахунковий момент за четвертою теорією міцності:

3. Визначимо діаметр вала, якщо . Для цього скористаємося умовою міцності:

Спочатку визначимо момент опору згинанню:

Момент опору згинанню для круглого поперечного перерізу:

Звідки визначимо діаметр валу:

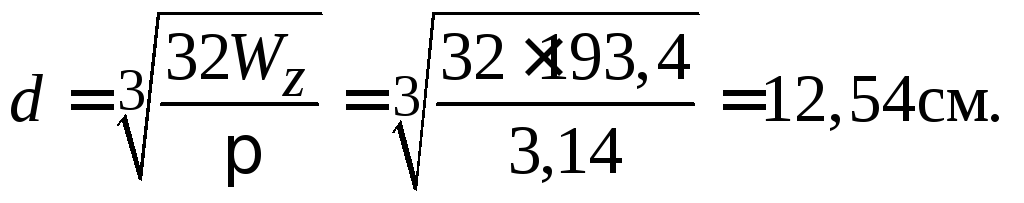
Отримане значення діаметра валу округляємо до найближчого більшого цілого числа, що є кратним п’яти. Остаточно приймаємо діаметр вала 15 см.

Задача № 11

Розрахунок на міцність валів при одночасній дії згину та кручення

Вихідні дані:

схема – 2 (рис. 23); потужність частота обертання; геометричні розміри:,,,,; допустиме напруження

Рис. 23. Розрахункова схема вала, епюри крутного та згинальних моментів

Розв’язання

1. За відомими потужністю та частотою обертання визначимо обертальні моменти на шківах:

Оскільки

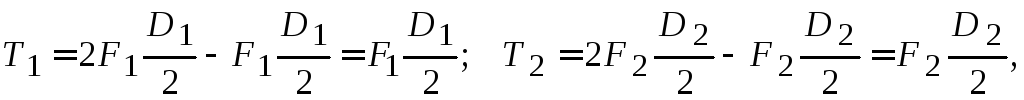
то зусилля натягу в пасках дорівнюють:

2. Обчислимо згинальні сили:

– у вертикальній площині

– у горизонтальній площині

3. Виконаємо розрахунок вала на вертикальне навантаження.

На підставі симетрії опорні реакції однакові й дорівнюють:

Знайдемо значення згинальних моментів у перерізах, де прикладені сили :

4. Виконаємо розрахунок вала на горизонтальне навантаження.

Для визначення опорних реакцій складемо рівняння рівноваги.

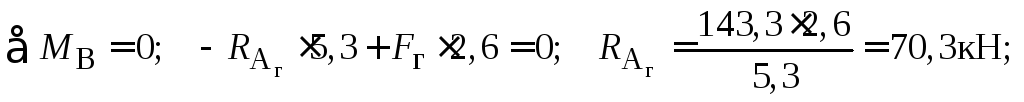
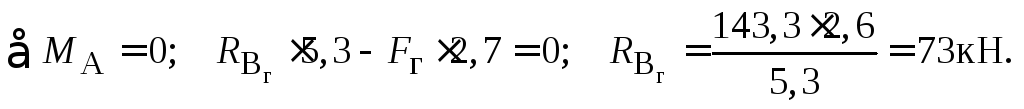
Перевіримо правильність визначення опорних реакцій:

Визначимо ординати згинальних моментів у перерізах, де прикладені сили та:

Значення результуючого згинального моменту в перерізах визначимо за формулою:

З аналізу побудованих епюр видно, що небезпечним буде переріз 2, у якому

Визначимо розрахунковий момент за третьою теорією міцності:

Умова міцності при згинанні має вигляд:

Визначимо діаметр вала

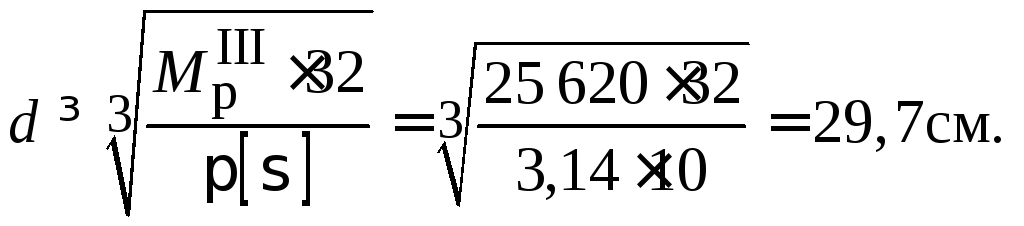
Остаточно приймаємо

Задача № 12

Добір площі поперечного перерізу стиснутого стержня

Вихідні дані:

схема – 1, форма перерізу – коробчастий переріз, що складається із чотирьох нерівнобічних кутиків, довжина стержня навантаженнярозрахунковий опір(для студентів будівельних спеціальностей), допустиме напруження(для студентів усіх інших спеціальностей).

а

б

Рис. 24. Розрахункові схеми (див. також с. 34): а – схема закріплення стержня, б – форма поперечного перерізу, в – схема кутика

в

Рис. 24. Розрахункові схеми (закінчення)

Розв’язання

Розрахунки виконуємо методом послідовних наближень.

Використаємо умову стійкості:

де – площа перерізу;

–коефіцієнт зменшення розрахункового опору;

–розрахунковий опір.

Визначимо площу поперечного перерізу одного кутика

Виконаємо нульове наближення, приймаючи

За сортаментом з табл. Д.2 обираємо кутик 65405 з такими геометричними характеристиками:

Визначимо мінімальний радіус інерції за формулою:

Знайдемо гнучкість стержня:

За табл. Д.5 значень визначимо коефіцієнт зменшення основного розрахункового опору: гнучкістьгнучкість

За формулою лінійної інтерполяції визначимо коефіцієнт зменшення розрахункового опору для гнучкості :

Визначимо дійсне напруження

та допустиме напруження на стійкість

Стержень перевантажено на 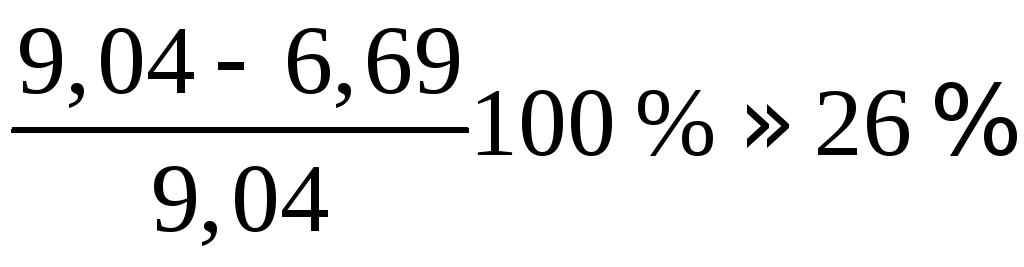, тому покращимо добір перерізу шляхом збільшення площі перерізу й зробимо таке наближення.

I наближення. Коефіцієнт зменшення розрахункового опору:

Площа поперечного перерізу

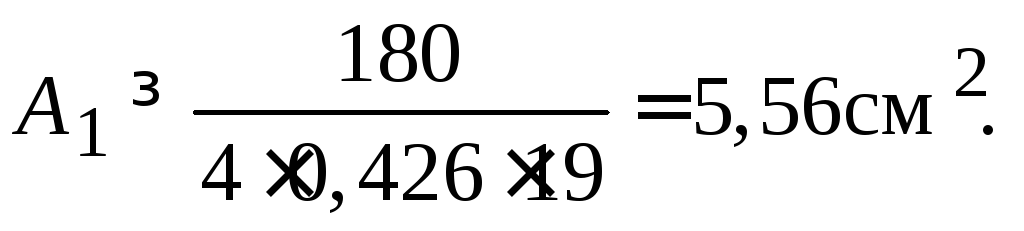
За сортаментом табл. Д.1 обираємо кутик, близький за значенням до площі поперечного перерізу, а саме кутик 70455 з геометричними характеристиками

Мінімальний радіус інерції:

Визначимо гнучкість стержня

За табл. Д. 5 значеньобираємо:

Перевірка напружень:

дійсне напруження

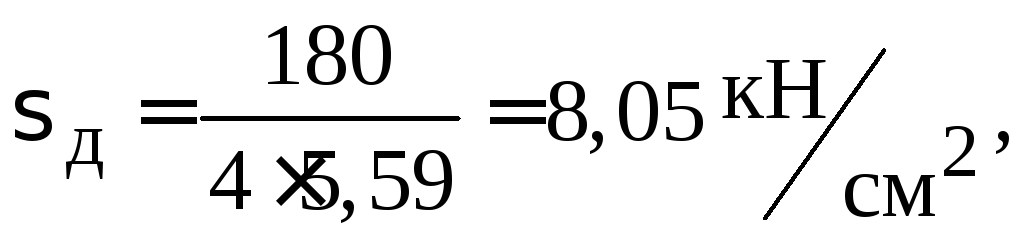
допустиме напруження на стійкість

Стержень недовантажено на

Остаточно приймаємо кутик 70455 з площею поперечного перерізу

Визначаємо критичну силу:

тоді коефіцієнт запасу стійкості дорівнює:

Задача № 13

Розрахунки на міцність та жорсткість балок при змушених коливаннях як систем з одним степенем вільності

Вихідні дані:

схема – 2; балка складається із двох двотаврів № 24 , довжина балки; вага двигуната величина незрівноваженої маси; ексцентриситет; частота обертання ротора двигуна.

Рис. 25. Розрахункова схема та епюра згинальних моментів