
дополнительно для заочников по матем
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
1 1 |
4 |
|
7 |
|
1 1 |
|
4 |
|
|
|
7 |
|
1 1 |
4 |
|
|
7 |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 − 2 2 |
|
− 2 |
|
~ |
|
0 1 |
|
|
−1 |
|
1 |
|
~ |
|
0 1 |
−1 |
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 −1 |
|
3 |
|
|
|
0 −1 |
− |
9 |
|
|
|
|
|
|
|
0 0 |
−10 |
|
−10 |
|
|||||||||
|
|
|
|
|
|
−11 |
|
|
|
|
||||||||||||||||||||
Соответствующая диагональная система уравнений имеет вид |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
λ1 + λ2 + 4λ3 = 7, |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
λ2 |
− λ3 =1, |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
−10λ3 = −10. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решая эту систему, получаем: λ1 =1, |
λ2 = 2, |
λ3 =1. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Таким |
образом, |
|
λ = a + 2 |
|
+ |
c |
, |
т.е. |
вектор |
|
|
|
|
||||||||||||||
|
|
|
b |
d |
в |
базисе |
||||||||||||||||||||||||
a, |
|
, c имеет координаты 1, 2, 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: (1, 2, 1). |
||||||
|
|
|
Задание 3. Матрица системы имеет вид |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Она невырожденная, так как соответствующий ей определитель
1 0 −1
∆ = 1 1 1 =1 ≠ 0 .
0 1 3
Следовательно, решение системы может быть найдено по формуле
X = A−1B , где Х – матрица, состоящая из неизвестных, В – матрица, состоящая из свободных членов, А-1 – обратная матрица для матрицы А. Обратную матрицу А-1 найдем по формуле
42
|
|
|
A |
A |
A |
|
|
|
1 |
|
11 |
21 |
31 |
|
|
A−1 = |
A |
A |
A |
|
|||
|
|||||||
|
∆ |
12 |
22 |
32 |
|
||
|
|
|
A |
A |
A |
|
|
|
|
|
13 |
23 |
33 |
|
|
Определим алгебраические дополнения Аik элементов данной матрицы. Получим
A11 = |
|
1 1 |
|
= 2, |
A21 |
= − |
|
0 −1 |
|
|
|
= −1, |
A31 |
= |
|
|
|
0 −1 |
|
=1, |
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|||||||||
A12 |
= − |
|
1 1 |
|
= −3, A22 |
= |
|
1 −1 |
|
=3, A32 = − |
|
1 −1 |
|
= −2 , |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||||||
A13 |
= |
|
1 1 |
|
=1, A23 = − |
|
1 0 |
|
= −1, A33 |
= |
|
1 0 |
|
=1. |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
−1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A−1 = |
−3 3 |
|
|
|
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
−1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В данном случае матричное равенство Х = А-1В может быть записано в виде
x |
|
|
|
2 |
−1 |
1 |
|
|
2 |
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
= |
|
−3 3 − 2 |
|
|
|
6 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
−1 |
1 |
|
|
|
5 |
|
x3 |
|
|
|
|
|
|
|
|||||
откуда
x1 = 2 2 −1 6 +1 5 =3, x2 = −3 2 + 3 6 − 2 5 = 2, x3 =1 2 −1 6 +1 5 =1.
Ответ: (3, 2, 1)
43
Задание 4. Пусть х1 – количество единиц проданного товара А, а х2 – количество единиц проданного товара В. Система неравенств, удовлетворяющая ограничениям задачи имеет вид:
0,4x |
+ 0,3x |
|
≤300, |
4x + |
3x |
|
≤3000, |
||
|
1 |
|
2 |
≤180, |
|
1 |
|
2 |
≤1800, |
0,2x1 |
+ 0,3x2 |
2x1 + |
3x2 |
||||||
|
80x1 |
+ 40x2 ≥32000, или |
|
|
x2 ≥800, |
||||
|
2x1 + |
||||||||
|
x |
|
|
≥ 0, |
|
x |
|
|
≥ 0, |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
x2 ≥ 0. |
|
|
x2 ≥ 0. |
||||
|
|
|
|
||||||
Заменим знаки неравенств на знаки равенств, получим следующую систему линейных уравнений:
4x1 + 3x2 |
=3000, |
|||
2x |
+ 3x |
2 |
=1800, |
|
|
1 |
|
|
|
|
|
+ x2 =800, |
||
2x1 |
||||
|
x |
|
= 0, |
|
|
1 |
|
|
|
|
|
x2 = 0. |
||
|
|
|||
Построим граничную прямую 4х1+ 3х2 = 3000. Она делит плоскость х1 0 х2 на две полуплоскости. Та из них, которая содержит начало координат, и есть область решений неравенства 4x1 + 3x2 ≤3000 ,
так как координаты точки О (0, 0) удовлетворяют данному неравенству (4 0 + 3 0 <3000). Аналогично построим граничные прямые, соот-
ветствующие остальным неравенствам системы. Стрелками укажем полуплоскости, являющиеся областями решений данных неравенств.
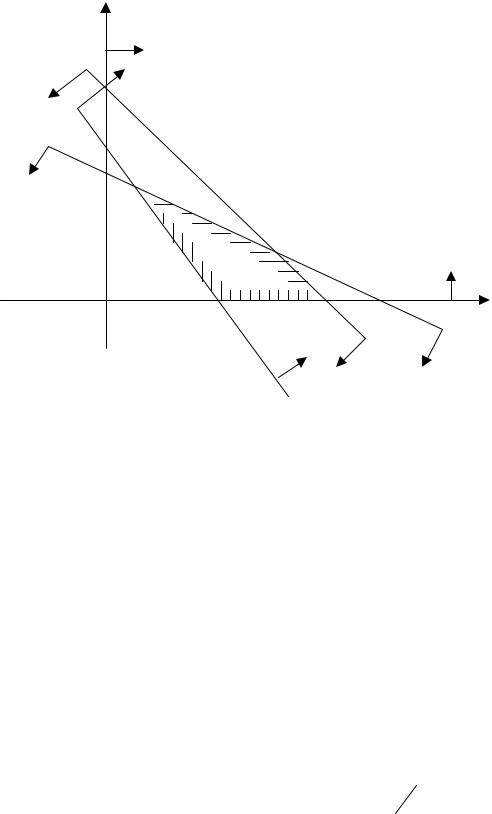
|
|
|
|
44 |
х2 |
|
|
|
|
100 |
|
|
|
|
800 |
|
|
|
|
600 |
A |
|
|
|
|
|
B |
|
|
|
D |
|
C |
|
0 |
400 |
750 |
900 |
х1 |
Пересечение отмеченных полуплоскостей – многоугольник |
АВСD яв- |
|||
ляется искомой областью допустимых вариантов товарооборота. |
||||
Задание 5. |
|
|
||
1. lim |
3x2 |
− 2x −8 |
. |
|
2x2 |
−5x + 2 |
|||
x→x0 |
|
|||
а) х0 = 4. Данная функция элементарная и точка 4 принадлежит ее области определения, следовательно, предел функции в точке 4 равен ее значению в этой точке (по теореме о пределе элементарной функции):
lim |
3x2 − 2x −8 |
= |
3 42 − 2 4 −8 |
= |
|
32 |
= |
16 |
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
14 |
|
7 |
|
||||||
x→4 |
2x2 −5x + 2 2 42 −5 4 + 2 |
|
|
|
|
16 . |
|||||
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
б) х0 = 2. Теорему о пределе элементарной функции здесь при- |
|||||||||||
менить нельзя, так как в точке |
2 знаменатель рассматриваемой дроби |
||||||||||
обращается в нуль. Имеем неопределенность вида |
0 |
0 |
. Так как при |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|

45
х = 2 числитель и знаменатель дроби обращаются в нуль, то многочлены 3x2 − 2x −8 и 2x2 −5x + 2 делятся без остатка на х – 2 (в
силу известного из алгебры следствия из теоремы Безу).
Выполним это деление, предварительно разложив числитель и знаменатель на множители. Получим
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3x2 − 2x −8 |
|
3 x + |
|
|
|
|
3x + 4 |
|
3 2 + 4 |
|
10 |
|
|||||
|
|
|
|
|
|
|
||||||||||||
lim |
= lim |
|
3 (x − 2) |
= lim |
= |
= |
. |
|||||||||||
2x2 −5x + 2 |
|
1 |
|
2x −1 |
2 |
2 |
−1 |
|
3 |
|||||||||
x→2 |
x→2 |
x→2 |
|
|
|
|||||||||||||
|
|
|
2 x − |
|
|
(x − 2) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: 103 .
в) х0 = ∞ . В данном случае имеем неопределенность вида ∞∞ .
Разделим числитель и знаменатель дроби на высшую степень х (в данном случае на х2), а затем воспользуемся теоремами о пределах функций
|
|
|
3x |
2 |
− 2x −8 |
|
3 |
− 2 |
x |
− 8 |
|
3 |
|
|
|
|
lim |
|
|
= lim |
|
|
x2 |
= |
. |
|
|||||
|
|
2x2 −5x + 2 |
|
− 5 |
|
+ 2 |
|
|
|||||||
|
x→∞ |
|
x→∞ 2 |
x |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
Ответ: 3 . |
|
|
1 − cos6x |
|
|
|
|
|
|
|
|
|
|
|
2 |
||
2. lim |
|
|
. При x →0 |
числитель и знаменатель дроби |
|||||||||||
x( 4 + x − |
|
|
|||||||||||||
x→0 |
2) |
|
|
|
|
|
|
|
|
0 . Чтобы |
|||||
стремятся к нулю, |
т.е. |
мы имеем неопределенность вида |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
раскрыть эту неопределенность, избавимся от иррациональности в зна-
менателе, умножив числитель и знаменатель дроби на |
( 4 + x + 2), |
||||||||
числитель преобразуем по формуле 1 − cos 6x = 2sin 2 3x и |
воспользу- |
||||||||
емся известным пределом lim |
sin x |
=1. Таким образом, |
|
|
|||||
x |
|
|
|||||||
|
|
|
x→0 |
|
|
|
|
||
lim |
1 |
− cos6x |
|
= lim |
2sin2 3x( 4 |
+ x + 2) |
= |
|
|
x( |
4 + x − |
2) |
|
4 + x + |
|
||||
x→0 |
|
x→0 x( 4 + x − 2)( |
2) |
|
|||||
46
lim |
2sin2 |
3x( 4 + x + 2) |
= 2lim( 4 |
+ x + 2) lim |
sin2 3x |
= |
||||
|
|
|
x2 |
|
x2 |
|||||
x→0 |
|
|
|
|
x→0 |
|
x→0 |
|
||
|
|
sin 3x 2 |
|
sin 3x |
2 |
2 |
|
|
||
=8 lim |
|
|
9 = 72lim |
|
= 72 1 = 72. |
|
||||
|
x→0 |
3x |
|
x→0 3x |
|
|
|
Ответ: 72. |
||
|
|
|
|
|
|
|
|
|
|
|
|
2n |
−1 3n−2 |
|
|
|
|
∞ |
|
||
3. lim |
|
|
|
. Имеем неопределенность вида 1 |
. Выраже- |
|||||
|
|
|||||||||
n→∞ 2n |
+ 3 |
|
|
|
|
|
|
|||
ние, стоящее под знаком предела, преобразуем к такому виду, чтобы можно было воспользоваться вторым замечательным пределом:
2n −1 |
3n−2 |
|
|
|
|
|
|
2n |
− |
1 |
|
|
|
3n−2 |
|
|
|
|
|
|
− 4 |
|
|
3n−2 |
= |
|
||||||||||||||||||
lim |
|
|
|
|
|
|
= lim 1 + |
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
= lim 1 + |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2n |
+ |
3 |
|
|
|
|
|
|
2n + |
|
|
||||||||||||||||||||||||||||
n→∞ 2n + 3 |
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
n→∞ |
|
3 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2n+3 |
|
−4 |
|
(3n−2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
− 4 |
|
|
|
2n+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
−4 |
|
|
|
|
|
|
|
|
= e |
−6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= lim |
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2n + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n→∞ |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n+3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 4(3n − 2) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 |
|
= e и |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
lim 1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
= −6 |
|
|
||||||||||||||||
|
|
|
|
|
|
2n + |
|
|
|
|
|
|
|
|
|
2n |
+ 3 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
n→∞ |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
Ответ: −6 . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Задание 6. |
Эластичность спроса относительно цены Ep(q) опре- |
|||||||||||||||||||||||||||||||||||||||||
деляется |
|
по формуле |
|
|
|
|
|
|
Ep (q) = |
|
p |
|
′ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
q |
q ( p) . Рассмотрим функцию |
|||||||||||||||||||||||||||||||||||
|
5 p + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
q = |
. Найдем производную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
p −1 |
|
|
5( p −1) −(5 p + 2) |
|
|
|
5 p −5 −5 p − 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
′ |
|
|
|
|
|
|
|
7 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
q ( p) = |
|
|
|
|
|
( p −1)2 |
|
|
|
|
|
= |
|
|
|
|
( p −1)2 |
|
|
= − |
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p −1)2 |
||||||||||||||||||||||||
Тогда |
|
Ep (q) = − |
p( p −1) |
|
|
|
|
7 |
|
|
|
= − |
|
|
|
7 p |
|
|
|
|
. |
|
|
|
|
|||||||||||||||||||
|
(5 p + 2) |
( p −1)2 |
|
|
(5 p + 2)( p −1) |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
При р = 2 |
получаем |
E2 |
( p) = − |
14 |
|
= − |
7 |
≈ −1,17% . Это означает, что |
||||||||||||||||||||||||||||||||||||
12 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||||
если цена возрастет на 1 % |
(от 2 до 2,01), то спрос на товар уменьшит- |
|||||||||||||||||||||||||||||||||||||||||||
ся приблизительно на 1,17 %. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47 |
|
|
Задание 7. y = |
|
x |
. |
|
|
|
|
|
|
||||||||
|
(x −1)2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Исследование функции проводим по следующей схеме: |
|
||||||||||||||||
|
1. Находим область определения функции. |
|
|
|||||||||||||||
|
Функция не определена лишь в точке х = 1, в которой знамена- |
|||||||||||||||||
тель обращается в нуль. Следовательно, |
D( f ) = (−∞, 1) (1, + ∞). |
|
||||||||||||||||
|
2. Исследуем функцию на четность и нечетность. Функция не |
|||||||||||||||||
является ни четной, ни нечетной, так как |
|
|
|
|||||||||||||||
|
f (−x) = |
− x |
|
|
= − |
− x |
|
и f (−x) ≠ f (x), f (−x) ≠ − f (x). |
||||||||||
|
(−x −1)2 |
(x +1)2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3. Исследуем функцию на непрерывность и определим верти- |
|||||||||||||||||
кальные асимптоты. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Исследуем поведение функции в окрестности точки х = 1. Функ- |
|||||||||||||||||
ция имеет разрыв второго рода в точке х = 1, причем |
|
|
||||||||||||||||
lim |
x |
|
|
= +∞, |
lim |
|
x |
|
|
= +∞. Следовательно, прямая х = 1 яв- |
||||||||
(x −1)2 |
(x −1)2 |
|||||||||||||||||
x→1−0 |
|
|
x→1+0 |
|
|
|
|
|
||||||||||
ляется |
вертикальной |
|
асимптотой |
графика |
функции |
при |
||||||||||||
x →1 − 0 |
и |
|
x →1 + 0 . В каждой точке области определения функция |
|||||||||||||||
непрерывна как элементарная.
4.Находим точки пересечения кривой с осями координат. Кривая проходит через начало координат, так как у = 0 при х = 0. Других точек пересечения с осями координат нет.
5.Определим точки экстремума и интервалы возрастания и убывания функции.
Находим производную данной функции
y |
′ |
|
(x −1)2 − 2x(x −1) |
|
|
(x −1)(x −1 − 2x) |
|
(x +1) |
|
||
= |
|
(x −1)4 |
= |
(x −1)4 |
= − (x −1)3 . |
||||||
|
|
||||||||||
Решаем уравнение |
y′= 0, т.е. |
|
|
|
|
|
|||||
|
|
|
|
− |
x +1 |
= 0 x = −1. |
|
|
|
||
|
|
|
|
(x −1)3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
Таким образом, х = –1 ─ критическая точка первого рода. Производная не определена в точке х = 1. Однако, эта точка не является критической, так как в ней не определена и сама функция.
Найденная критическая точка х = –1 разбивает область определения функции на три интервала: (−∞, −1), (−1, 1) и (1, + ∞).

48
Исследуем знак y′ на каждом из этих интервалов. Результаты исследования пометим в табл. 1.
|
|
|
|
|
|
Таблица 1 |
|
х |
(−∞, 1) |
|
−1 |
(−1, 1) |
|
(1, + ∞) |
|
y′ |
– |
|
0 |
+ |
|
– |
|
у |
|
|
− 1 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
min |
|
|
|
|
Из табл. 1 следует, что функция в интервалах (−∞, −1) |
и (1, + ∞) убы- |
||||||
вает, так как y′< 0 ; |
в интервале (−1,1) возрастает, так как y′> 0 . |
||||||
При переходе через критическую точку первого рода х = –1 слева направо производная меняет знак с минуса на плюс. Следовательно,
в точке х = –1 функция имеет минимум, равный f (−1) = −14 .
6. Определяем точки перегиба и интервалы выпуклости, вогнутости. Находим вторую производную:
|
′′ |
|
|
|
|
x +1 |
|
′ |
(x −1) |
3 |
−3(x −1) |
2 |
(x |
+1) |
|
||||
y |
|
− |
|
|
|
|
|
= |
|||||||||||
|
|
3 |
|
|
|
|
|
|
6 |
|
|
|
|||||||
|
= |
|
(x −1) |
= − |
|
|
|
(x −1) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
= − |
|
(x −1)2 (x −1 −3x −3) |
= |
|
2(x + 2) |
. |
|
|
|
||||||||
|
|
|
|
|
(x −1)6 |
|
|
(x |
−1)4 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решаем уравнение |
|
|
y′′= 0 , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2(x + 2) = |
0 |
|
|
x = −2 . |
|
|
|
|
|||||
|
|
|
|
|
|
(x −1)4 |
|
|
|
|
|
|
|
|
|
|
|
||
Итак, х = –2 |
– критическая точка второго рода. Других критических |
||||||||||||||||||
точек нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найденная критическая точка х = –2 |
разбивает область опреде- |
||||||||||||||||||
ления на следующие интервалы: |
(−∞, − 2), |
(−2, 1), |
(1, + ∞). |
||||||||||||||||
Определим знак y′′ |
на каждом из этих интервалов. Результаты |
||||||||||||||||||
поместим в табл. 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
х |
|
(−∞, − 2) |
|
|
− 2 |
|
|
|
|
|
(−2, 1) |
|
(1, + ∞) |
|
|||
y′′ |
|
– |
|
|
0 |
|
|
|
|
|
|
+ |
|
+ |
|
||
y |
|
Выпукла |
|
|
− |
2 |
|
|
|
|
Вогнута |
|
Вогнута |
|
|||
|
|
∩ |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перегиб |
|
|
|
|
|
|
|
|
|
|
||
Из табл. 2 |
видно, что в интервале (−∞, − 2) кривая выпукла, так как |
||||||||||||||||
y′′< 0 ; а в интервалах (−2, 1) и |
(1, + ∞) |
– вогнута, так как y′′> 0 . |
|||||||||||||||
При переходе через критическую точку второго рода |
х = –2 сле- |
||||||||||||||||
ва направо вторая производная |
меняет |
|
знак. Следовательно, точка |
||||||||||||||
х = –2 является точкой перегиба, причем f (−2) = − 2 . |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
7. Определяем горизонтальные асимптоты. Так как |
|
|
|||||||||||||||
|
|
|
|
|
x |
|
|
1 |
|
|
|
|
|
|
|||
|
|
lim |
|
|
= lim |
|
|
x |
|
|
= 0, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
|
x→±∞ (x −1)2 |
x→±∞ |
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то прямая |
у = 0 является горизонтальной асимптотой графика функ- |
||||||||||||||||
ции при x → +∞ и при |
x → −∞. |
|
|
|
|
|
|
|
|
|
|||||||
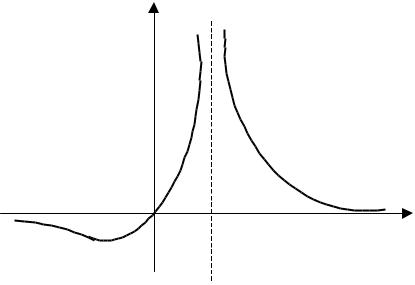
Построим график функции
|
у |
|
-2 |
-1 |
1 |
|
0 |
х |

50
Задание 8. Обозначим через х радиус основания цилиндра, а через у высоту цилиндра. Тогда объем цилиндра будет равен
V = πx2 y
у
2х
Получим функцию двух переменных х и у. Эту функцию легко преобразовать в функцию одной переменной. По условию задачи периметр осевого сечения цилиндра равен а, т.е. 4х + 2у = а. Отсюда
y = a − 4x . Следовательно
2
V = πx2 |
a − 4x |
= |
π x2 |
(a − 4x). |
|
|
||
2 |
|
|
||||||
|
|
2 |
|
|
|
|||
Из условия задачи следует, что |
|
|
|
|
|
|
||
x > 0 |
x > |
0 |
|
|
|
|
a |
|
|
|
|
|
0 |
< x < |
|||
|
a − |
4x |
|
|
||||
> 0 |
4 |
|||||||
y > 0, т.е. |
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
||
Итак, требуется найти наибольшее значение функции
V = |
π |
x |
2 |
(a − 4x) на интервале |
|
a |
|
2 |
|
0, |
|
. Найдем стационарные точки |
|||
|
|
||||||
|
|
|
|
|
4 |
||
данной функции, содержащейся в рассматриваемом интервале. Вычис-
лим V ′= |
π |
(2ax −12x2 ) и решим уравнение V ′= 0 , т.е. |
||||||
2 |
||||||||
|
|
|
πx(a − 6x) = 0 . |
|
|
|
||
Следовательно, х = 0 или |
x = |
a |
|
|
a |
|||
6 |
. На интервале |
0, |
|
рассматривае- |
||||
|
||||||||
|
|
|
|
|
|
4 |
||
мая функция имеет лишь одну стационарную точку x = a6 . Исследуем
