симплексные таблицы, преобразование

Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:

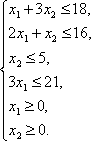
Решение:

I итерация:

1 этап: формирование исходной симплекс-таблицы.

Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.

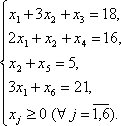
В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:

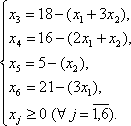
Приведем целевую функцию к следующему виду:

На основе полученной задачи сформируем исходную симплекс-таблицу:

Таблица 5.3

Исходная симплекс-таблица

СП БП				Оценочные отношения
	18	1	3
	16	2	1
	5	0	1
	21	3	0
	0	–2	–3

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

3 этап: проверка совместности системы ограничений ЗЛП.

На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

4 этап: проверка ограниченности целевой функции.

На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).

5 этап: проверка допустимости найденного базисного решения.

Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

6 этап: проверка оптимальности.

Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.

8 этап: определение разрешающего элемента.

8.1. Определение разрешающей колонки.

Так как найденное базисное решение допустимое, то поиск разрешающей колонки будем производить по следующей схеме: определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.3, таких колонок две: колонка «х1» и колонка «х2». Из таких колонок выбирается та, которая содержит наименьший элемент в строке целевой функции. Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.

8.2. Определение разрешающей строки.

Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.

Таблица 5.4

Исходная симплекс-таблица

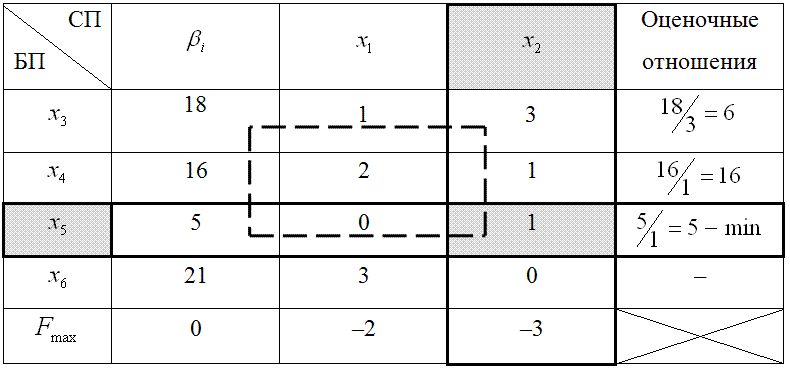
В таблице 5.4 наименьшее положительное оценочное отношение соответствует строке «х5», следовательно, она будет разрешающей.

Элемент, расположенный на пересечение разрешающей колонки и разрешающей строки, принимается в качестве разрешающего. В нашем примере – это элемент , который расположен на пересечении строки «х5» и колонки «х2».

9 этап: преобразование симплекс-таблицы.

Разрешающий элемент показывает одну базисную и одну свободную переменные, которые необходимо поменять местами в симплекс-таблице, для перехода к новому «улучшенному» базисному решению. В данном случае это переменные х5 и х2, в новой симплекс-таблице (таблице 5.5) их меняем местами.

9.1. Преобразование разрешающего элемента.

Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:

Полученный результат вписываем в аналогичную клетку таблицы 5.5.

9.2. Преобразование разрешающей строки.

Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.

9.3. Преобразование разрешающей колонки.

Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.

9.4. Преобразование остальных элементов симплекс-таблицы.

Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника».

К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки «», условно обозначим его «х3». В таблице 5.4 мысленно вычерчиваем прямоугольник, одна вершина которого располагается в клетке, значение которой преобразуем (т.е. в клетке «х3»), а другая (диагональная вершина) – в клетке с разрешающим элементом. Две другие вершины (второй диагонали) определяются однозначно. Тогда преобразованное значение клетки «х3» будет равно прежнему значению данной клетки минус дробь, в знаменателе которой разрешающий элемент (из таблицы 5.4), а в числителе произведение двух других неиспользованных вершин, т.е.:

«х3»: .

Аналогично преобразуются значения других клеток:

«х3 х1»: ;

«х4»: ;

«х4 х1»: ;

«х6»: ;

«х6 х1»: ;

« »: ;

« х1»: .

В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).

II итерация:

1 этап: составление симплекс-таблицы.

По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

Таблица 5.5

Симплекс-таблица II итерации

СП БП				Оценочные отношения
			–(3/1)=–3
			–(1/1)=–1
	5/1=5	0/1=0	(1)–1=1
			–(0/1)=0
			–(–3/1)=3