9.Формулы Френеля

Интенсивность отраженной и преломленной волн

РИС.28-1

Способ обобщения полученных результатов:

-если фазы колебаний не скоррелированы (случайны), то ;

-если фазы скоррелированы (постоянная разность фаз), то .

А. Свет поляризован в плоскости падения .

Записываем условие равенства тангенциальных компонент на границе раздела:

,

.

Поскольку эти условия должны выполняться в любой момент времени и при любом положении границы раздела, то можно экспоненты не записывать и пользоваться выражениями для амплитуд:

,

.

Делим второе уравнение на первое:

,

,

,

.

Переписываем эту формулу со знаком - поляризация в плоскости падения:

1930. 

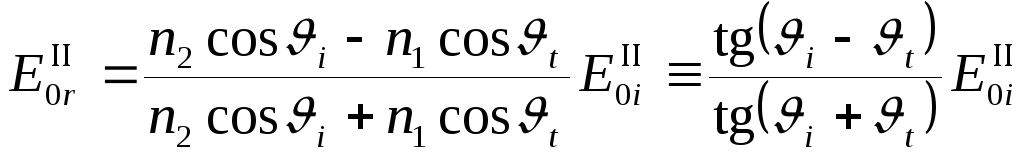
(здесь учтено, что ).

Ищем амплитуду преломленной волны. Для этого складываем первое и второе уравнения:

.

1930. .

Б. Поляризация поперек плоскости падения

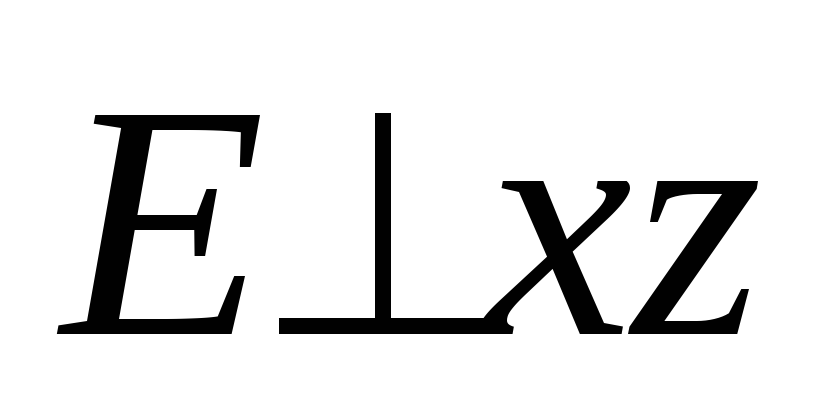
Те же граничные условия переписываем для этой поляризации:

,

.

Поделив второе уравнение на первое, находим соотношение амплитуд падающей и отраженной волн:

,

,

,

1930. .

Складывая первое и второе уравнения, получаем связь между амплитудами падающей и преломленной волн:

.

(4) .

Получили формулы Френеля – амплитудные коэффициенты отражения и прозрачности, выраженные через угол падения и свойства границы раздела.

При формулы Френеля переходят в известные соотношения для отражения и прохождения при нормальном падении.

Случай, когда плоскость поляризации составляет угол с плоскостью падения:

. РИС.28-2

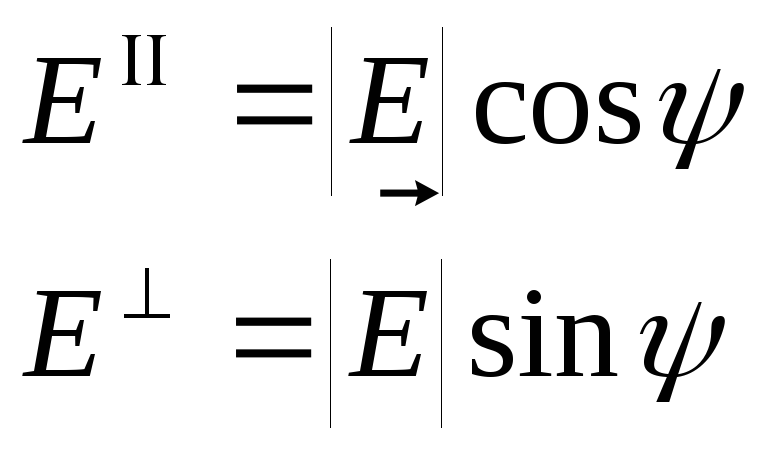
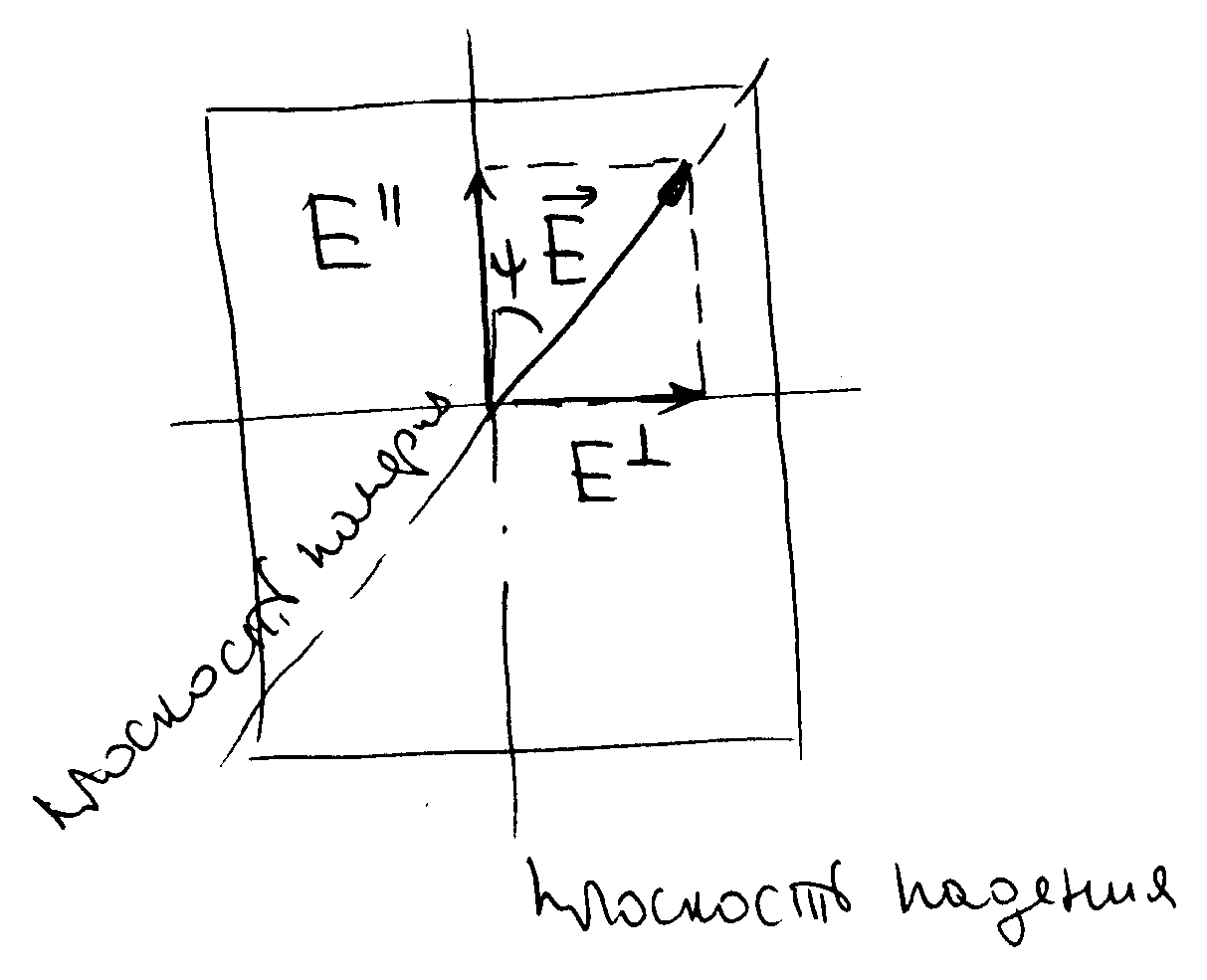
Угловая зависимость отражения электромагнитных волн

Энергетические коэффициенты отражения:

; .

15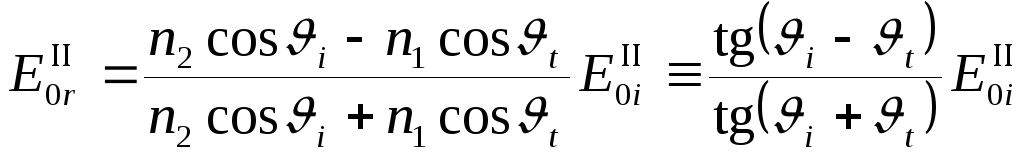