-
Отражение и преломление электромагнитных волн на границах раздела
В однородной среде (
)
электромагнитные волны распространяются
прямолинейно и не затухают, если
электропроводность
.
При наличии неоднородностей электромагнитная
волна отражается, преломляется,
рассеивается.
Простейший случай: резкая граница раздела двух диэлектриков (заряд на поверхности, ток по поверхности равны нулю). Нормальное падение.
РИС.26-8
Условие на границе
раздела:
,
.
Падает на границу плоско поляризованная монохроматическая волна:
,
,
.
Падающая волна:
,
,
.
Отраженная волна:
,
,
.
Преломленная
(прошедшая) волна:
,
,
.
Из условия непрерывности тангенциальных компонент на границе раздела следует:
- сюда подставляем выражения для волн.
Получаем:
;
.
Полученная система
должна удовлетворяться при любых
,
в том числе при
.
Отсюда:
;
.
Сокращая на
- поскольку система должна удовлетворяться
во все моменты времени, имеем:
.
Делим (2) на (1):
.
Отсюда легко вычислить связь амплитуд отраженной и падающей волн:
,
,
Фазовые соотношения:
{signзнак}.
Амплитудный коэффициент отражения:
.
Энергетический коэффициент отражения равен отношению среднего потока энергии в отраженной волне к среднему потоку энергии в падающей волне:
.
На опыте измеряется энергетический коэффициент отражения, поскольку все приемники реагируют на интенсивность волны, то есть на квадрат ее амплитуды.
Примеры:
1) Стекло-воздух:
;
.
2) Германий-воздух:
;
.
-
при
(металлы).
8 . Наклонное падение света на границу двух диэлектриков
РИС.27-6
Задача №1 – об углах отражения и преломления:
Плоская электромагнитная волна падает на границу раздела двух диэлектриков.
Падает волна
по произвольному направлению
,
определяемому направляющими углами
между
и осями
соответственно.
(здесь
,
,
).
З
десь
всюду (и впоследствии) мы подразумеваем
.
РИС.27-6
Теперь,
пользуясь этим общим выражением, запишем
падающую волну. Пусть она распространяется
так, что
(т.е. луч света лежит в плоскости
):
.
На направления распространения отраженной и преломленной (прошедшей) волн никаких ограничений не накладывается.
,
.
На границе –
равенство тангенциальных компонент
поля:
;
.
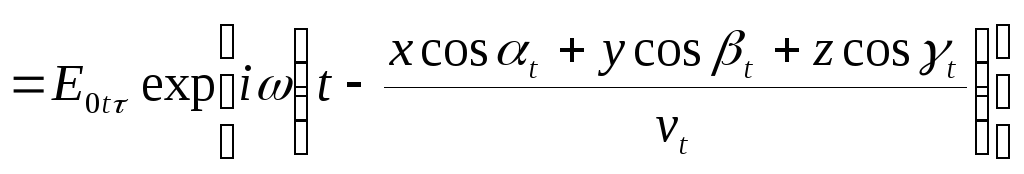Частота на
границе не меняется,
;
.
Граница
помещена на плоскость
,
уравнение упрощается:
.
Данное тождество выполняется при следующих условиях:
-
Сумма двух периодических функций (экспонент) будет периодической функцией (экспонентой) лишь в том случае, если аргумент однороден, то есть:
.
Первый вывод: векторы распространения
и
тоже лежат в плоскости
.
2)Второй вывод:
.
А)
;
по физическому смыслу – угол падения
равен «минус» углу отражения ;
б)
.
Возвращаясь
от направляющих углов
к углам (на Рис. 27.6)
,
и замечая, что
,
дополняют
до
,
т.е.
,
получаем:
- вывел Снеллиус (1580-1626), профессор
математики Лейденского университета.
Итак, исходя
из граничных условий для
и
в уравнениях Максвелла, мы получили
основные законы геометрической оптики:
- угол падения равен углу отражения;
- закон Снеллиуса.