Бесконечные пределы в интеграле записаны для общего случая и должны быть уточнены для конкретного сигнала. Если сигнал периодический, то его средняя за период t мощность равна

. (1.11)

Спектральное представление сигнала позволило определить эти же энергетические характеристики по спектрам сигналов. Для этого существуют равенства Парсеваля. Для непериодического сигнала

; (1.12)

для периодического

, (1.13)

где постоянная составляющая сигнала, А_n – амплитуда n-ой гармоники.

Значения в выражениях (1.10, 1.12) означает, что в создании энергии и мощности участвует бесконечный спектр частот. Если же заменить эти бесконечности на конечную величинуn и , то по формулам (1.11), (1.13) определится только часть мощности и энергии. Этим подходом можно воспользоваться при ограничении спектров сигналов.

Рассчитываем энергию сигнала показанного на рис.1.1 по формуле 1.10. Для этого вместо значения подставляем значения времени.

Определение практической ширины спектра сигнала. Ограничение практической ширины спектра сигнала по верхнему значению частоты _с по заданному энергетическому критерию осуществляется на основе неравенства: .

Где

, (1.14)

_c - искомое значение верхней граничной частоты сигнала.

Один из методов нахождение частоты среза по графику. Для этого в одной системе координат построим графики энергии равные W=Дж, W`(<sub>c</sub>), W''=W==Дж. Находим значение<sub>с</sub> по графику (рис. 1.7). Точка пересечения W`(_c) и W`` соответствует значению _с. Другой способ более точный нахождения частоты среза через равенство Парсеваля:

(1.15)

С помощью программы Mathcad решаем уравнение (1.15) и находим частоту среза которая равна _с=16845 рад/с.

Рис.1.7 График энергии сигнала №1

Энергия сигнала показанного на рис.1.2 рассчитываем, как и в предыдущем случае.

Частота среза сигнала показанного на рис.1.2 определяется также как и частота среза сигнала показанного на рис.1.1. И она равна _с=51000 рад/с.

Рис.1.8 График энергии сигнала №2

Энергия сигнала показанного на рис.1.3 рассчитываем по формуле 1.12 так как у данного сигнала известна граничная спектральная частота.

Частота среза сигнала показанного на рис.1.3 определяется также как и частота среза сигнала показанного на рис.1.1. И она равна _с=84920 рад/с.

Рис.1.9 График энергии сигнала №3

Дальнейший расчет ведем для треугольного сигнала т.к. у этого сигнала частота среза оказалась меньше чем у других.

_с=16845 рад/с.

2. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛА ДИСКРИТИЗАЦИИ И РАЗРЯДНОСТИ КОДА

Дальнейший расчет ведем для треугольного сигнала т.к. у этого сигнала частота среза оказалась меньше чем у других.

_с=16845 рад/с.

Интервал дискретизации t по времени определяем на основе теоремы Котельникова по неравенству:

t 1/(2F_в), (2.1)

где F_в=_с/(2) - верхнее значение частоты спектра сигнала.

F_в=16845/2=2.710³ Гц

t=1/2.710³=3.710^-4 с.

Необходимо, чтобы сигнал был представлен не менее чем четырьмя отсчетами. Для выполнения этого условия уменьшим интервал t:

t=0.0510^-3с, частота запуска АЦП F_д=1/t=1/0.0510^-3=20000 Гц.

Рис.2.1. График дискретизированного по времени сигнала

Следующими этапами преобразования сигнала являются квантование импульсных отсчетов по уровню и кодирование.

Разрядность кода определяется исходя из динамического диапазона квантуемых по уровню импульсных отсчетов. При этом в качестве верхней границы динамического диапазона Umax принимается напряжение самого большого по амплитуде отсчета.

Umax=0.05 В.

Нижняя граница диапазона:

Umin=Umax/K; (2.2)

K - заданный коэффициент.

Umin=0.05/26=0.002 В.

Дальнейший расчет ведем следующим образом.

Для самого малого по амплитуде импульсного отсчета Umin задается соотношение мгновенной мощности сигнала и мощности шума квантования:

=Umin2/Pшкв= 50;

Известно, что:

Pшкв=²/12; - шаг шкалы квантования.

=Umax/nкв; nкв - число уровней квантования.

Отсюда:

;

При использовании двоичного кодирования:

n_кв = 2m; m - разрядность кодовых комбинаций.

m = log n_кв;

m = log 51= 6.

Длительность элементарного кодового импульса и определяется исходя из интервала дискретизации t и разрядности кода m. Здесь необходимо ввести защитный интервал, под который отведем половину t. В итоге получим выражение:

_и = t/(2m); (2.3)

_и = 0.05·10^-3 /12 =41.7 мкс.

На основании полученного значения разрядности кода и интервала дискретизации выберем АЦП. Полученным значениям удовлетворяет микросхема К1107ПВ1. Характеристики микросхемы приведены в табл. 2.1.

Таблица 2.1 Технические характеристики АЦП

Серия	Разрядность выхода	Тип логики	Уровень 1, В	Уровень. 0, В	Fт, преобраз.
К1107ПВ1	6	ТТЛ	2.4	0.4	6.5 МГц

Для разработки математической модели цифрового сигнала примем четыре кодовых слова (коды четырех отсчетов).

Числовые константы сигнала определяются по формулам (2.4) и (2.5). Математическое ожидание:

. (2.4)

Дисперсия:

. (2.5)

Выбранная кодовая последовательность:

110011 100110 011010 001101

Вероятность нуля:

Вероятность единицы:

Рассчитаем математическое ожидание сигнала по (2.8).

В.

Дисперсия:

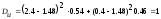В.

Рассчитаем функцию автокорреляции. При проведении расчетов воспользуемся возможностями программы MathCAD. Поступим следующим образом. Выпишем четыре последовательности кодов, которыми представляется дискретизированный сигнал; это будет последовательность нулей и единиц.

В среде MathCAD. создадим два вектора и. Далее воспользуемся функцией. После каждого измерения будем сдвигать кодовую последовательность вектораVy на один знак. Проведём семь расчётов. Результаты занесём в таблицу 2.2

Таблица 2.2 Функция автокорреляции кодового сигнала

, мкс	0	4.17	8.34	12.51	16.68	20.85	25.02	29.19
Corr	1	-7·10-3	-0.51	-0.175	0.329	0.161	-0.343	-7·10-3

В среде MathCAD по этой таблице сформируем два вектора Vt и Vk:

С помощью функции cspline(Vt, Vk) вычислим вектор VS вторых производных при приближении к кубическому полиному:

VS : = cspline (Vt, Vk)

.

Далее вычисляем функцию, аппроксимирующую функцию автокорреляции сплайн кубическим полиномом:

kor() : = interp (VS, Vt, Vk, ).

Рис.2.2 График функции автокорреляции

Спектральные характеристики кодированного сигнала находятся на основании интегрального преобразования Винера-Хинчина. В области действительной переменной оно имеет следующий вид:

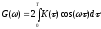. (2.6)

Здесь K() выше рассчитанная нормированная функция kor(), верхний предел T – последнее рассчитанное значение .

Решение интеграла произведём в среде MathCAD.

Спектр кодированного сигнала показан на рис.2.3.

Рис.2.3 Спектр кодированного сигнала

3. ХАРАКТЕРИСТИКИ МОДУЛИРОВАНОГО СИГНАЛА

Для передачи полезной информации в технике связи обычно используются модулированные сигналы. Они позволяют решить задачи уплотнения линий связи, электромагнитной совместимости, помехоустойчивости систем. Процесс модуляции является нелинейной операцией и приводит к преобразованию спектра канала. При гармоническом сигнале-переносчике это преобразование заключается в том, что спектр полезного сигнала переносится в область несущей частоты в виде двух боковых полос. Если переносчик импульсная последовательность, то такие боковые полосы расположены в окрестностях каждой гармоники переносчика. Значит, продукты модуляция зависят от полезного сигнала и от вида сигнала-переносчика.

Для определения спектра ЧМ- сигнала воспользуемся линейностью преобразования Фурье. Сигнал представлен в виде суммы двух АМ- колебаний с различными частотами несущих f1 и f2,

. (3.1)

Рис.3.1 Модулированный сигнал

К каждому такому сигналу применим преобразование Фурье и результирующий спектр определится как сумма спектров S1(j) и S2(j):

(3.2)

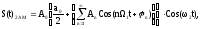(3.3)

где - частота первой гармоники.

Для того, чтобы наглядно показать полосы частот спектра с учетом того, что сдвига фаз нет, запишем (3.1) в упрощенном виде:

Так как сдвига фаз нет, принимаем .

Итоговый спектр ЧМ содержит несущие 1, 2, в окрестностях каждой из которых расположены боковые полосы, состоящие из комбинаций частот и.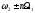

По заданию несущие частоты равны:

ω₁=5.510⁶ рад/с, ω₂=1.1310⁷ рад/с.

Определяем по формуле:

(3.4)

Анализируя правую часть выражения (3.4), определяем полосы частот гармоник сигнала.

Таблица 3.1 Полосы частот гармоник сигнала.

№ гармоники (n)	,	,	,	,	Амплитуда гармоник В
1	2	3	4	5	6
1	4.75106	6.25106	1.055107	1.205107	1.528
3	3.25106	7.75106	9.05106	1.355107	0.509
5	1.75106	9.25106	7.55106	1.505107	0.306

Амплитуды гармоник посчитаем по формуле:

, (3.5)

где В₀ – уровень логической единицы,

n – номер гармоники.

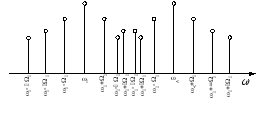
Рис. 3.2 Спектр колебания, модулированного по частоте сигнала

Итоговый спектр ЧМ сигнала состоит из двух несущих и двух боковых полос с частотами и.

Для практического использования спектр необходимо ограничить полосой . Ограничение проведем по пяти крайним боковым составляющим. Расчёт полосы частот спектра проведём по формуле:

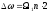. (3.6)

где n количество боковых составляющих.

дискретизация квантование сигнал связь

4. СОГЛАСОВАНИЕ ИСТОЧНИКА ИНФОРМАЦИИ С КАНАЛОМ СВЯЗИ

4.1 Источник информации

Выборки передаваемого сигнала это алфавит источника информации и вероятности букв этого алфавита равны друг другу. Такой источник имеет ряд информационных характеристик: количество информации в знаке, энтропию, производительность, избыточность. В дальнейшем нас будет интересовать производительность, которая характеризует скорость работы источника и определяется по следующей формуле:

, (4.1)

где энтропия алфавита источника,среднее время генерации одного знака алфавита.

Для введённого источника энтропия определяется при условии равенства вероятностей знаков алфавита, а среднее время равно интервалу между выборками. Подставим значения в (4.1).

.

4.2 Согласование источника с каналом

Рассмотрим принципы и предельные возможности непосредственного согласования дискретного источника сообщений с непрерывным каналом связи. Напомним, что в непрерывном канале надо знать плотности распределения случайных процессов сигналов, помех и их же условные плотности распределения. Это понятие вводится при моделировании канала связи и с точки зрения передачи сообщений нет большого противоречия в том, что источник принят дискретным, а канал непрерывный.

Будем считать канал гауссовым, то есть все статистики в нем имеют нормальное распределение. На входе канала, помимо сигнала, присутствует помеха типа «белый шум».

Предельные возможности согласования дискретного источника с непрерывным каналом определяются теоремой Шеннона.

Пропускная способность гауссова канала равна:

. (4.2)

где F_Д – частота дискретизации, определенная выше. Рп мощность помехи, определяется по заданной спектральной плотности мощности N₀ (дано в задании на курсовой проект) и полосе частот модулированного сигнала :

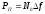. (4.3)

По этим формулам, пользуясь неравенством Шеннона , определим Р_С, обеспечивающую передачу по каналу.

Для определения Р_С примем пропускную способность канала равную:

.

Выделим из (4.2) Р_с.

,Вт. (4.4)

5. РАСЧЁТ ВЕРОЯТНОСТИ ОШИБКИ В КАНАЛЕ С АДДИТИВНЫМ БЕЛЫМ ШУМОМ

5.1 Определение вероятности ошибки

Вероятность ошибки P₀ зависит от мощности (или энергии) сигнала и мощности помех (в данном случае белого шума). Известную роль играет здесь и вид сигнала, который определяет статистическую связь между сигналами в системе. Расчёт вероятности ошибки, прежде всего, необходим при оптимальной схеме приёмника, т.е. наилучшей в смысле заданного критерия. В технике связи критерием является критерий Котельникова (оптимального наблюдателя). Согласно его требованиям полная вероятность ошибки должна быть минимальной.

Для реализации такого критерия служит оптимальная решающая схема. При равновероятных и взаимонезависимых сигналах решающая схема поэлементного приёма принимает решение независимо от решения относительно других символов и имеет вид:

(5.1)

Символ S_i над неравенством указывает на то, что решение принимается в пользу сигнала S_i. Из второй общей формулы можно получить простые записи с оговоркой тех или иных условий. Будем считать, что отсчёт времени начинается с началом k-го элемента сигнала, что C(t)=S(t) – приходящий полезный сигнал, и тогда условие правильной регистрации сигнала S_i(t) имеет вид:

. (5.2)