
- •Тема 4 потенціальна енергія деформації. Теорії міцності
- •4.1. Потенціальна енергія при об'ємному напруженому стані. Питома потенціальна енергія змінення форми
- •4.2. Оцінка міцності за відомим напруженим станом. Класичні теорії міцності
- •4.2.1. Теорія найбільших нормальних напружень
- •4.2.2. Теорія найбільших лінійних деформацій
- •4.2.3. Теорія найбільших дотичних напружень
- •4.2.4. Енергетична теорія міцності
- •4.2.5. Теорія міцності Мора
- •Де ;;;.
- •4.3. Тести до теми №4 “Потенціальна енергія деформації. Теорії міцності” Таблиця 4.1
Тема 4 потенціальна енергія деформації. Теорії міцності
4.1. Потенціальна енергія при об'ємному напруженому стані. Питома потенціальна енергія змінення форми
Потенціальною енергією деформації називається енергія, що накопичується в тілі при його пружніх деформаціях. Під дією зовнішнього статичного навантаження тіло деформується, точки прикладення зовнішніх сил переміщуються і потенціальна енергія положення зовнішніх навантажень зменшується на величину, що дорівнює роботі зовнішніх сил на викликаних ними переміщеннях. Енергія, загублена зовнішніми силами, не зникає, а перетворюється, в основному, у потенціальну енергію деформації тіла. Інша, незначна частина енергії розсіюється, головним чином, у вигляді тепла за рахунок різних процесів, що відбуваються в матеріалі при його деформації.
Обчислимо повну потенціальну енергію, що накопичується в елементарному паралелепіпеді при його пружній деформації. В якості об'єкта розглянемо елемент, наведений на рис.4.1.

Рис.4.1
Потенціальна енергія деформації накопичується у зворотній формі – у процесі розвантаження тіла вона знову перетворюється в енергію зовнішніх сил або кінетичну енергію. Повна потенціальна енергія, що накопичується в елементарному паралелепіпеді, дорівнює:
![]() (4.1)
(4.1)
Величину потенціальної енергії, що накопичується в одиниці об'єму матеріалу, прийнято називати питомою потенціальною енергією:
![]() .
(4.2)
.
(4.2)
Підставляючи в (4.2) вираз для відносної деформації з (3.73), одержуємо:
![]() (4.3)
(4.3)
Вираз
(4.3) записано для питомої потенціальної
енергії для випадку, коли відомі значення
головних напружень
![]() і деформацій
і деформацій![]() .
У тому випадку, якщо відомі неголовні
нормальні напруження
.
У тому випадку, якщо відомі неголовні
нормальні напруження![]() і
і![]() ,
дотичні напруження
,
дотичні напруження![]() ,
відповідні лінійні подовження
,
відповідні лінійні подовження![]() ,
,![]() і кутові деформації
і кутові деформації![]() ,
повна потенціальна енергія, що
накопичується в елементарному
паралелепіпеді, дорівнює:
,
повна потенціальна енергія, що
накопичується в елементарному
паралелепіпеді, дорівнює:
![]() (4.4)
(4.4)
Питома потенціальна енергія має вигляд:
![]() (4.5)
(4.5)
або
![]() .
(4.6)
.
(4.6)
Іноді питому потенціальну енергію зручно виразити через деформації:
![]() ,
(4.7)
,
(4.7)
де
![]() ;
;![]()
об'ємна деформація;
об'ємна деформація;
![]()
об'ємний модуль пружності (3.85).
об'ємний модуль пружності (3.85).
При
деформації елемента змінюється як його
об’єм, так
і форма (з куба він перетворюється на
паралелепіпед) (Рис.4.1). У зв'язку з цим
можна вважати, що повна питома потенціальна
енергія деформації
![]() складається з питомої потенціальної
енергії зміни об’єму
складається з питомої потенціальної
енергії зміни об’єму
![]() і питомої потенціальної енергії зміни
форми
і питомої потенціальної енергії зміни
форми![]() :
:
![]() (4.8)
(4.8)
Спочатку
обчислимо питому потенціальну енергію
зміни об’єму.
Для цього зробимо припущення про те, що
в різних елементах (Рис.4.2) при дії різних
головних напружень величина
![]() буде однаковою, якщо у елементів буде
однаковою зміна об’єму
[3].
буде однаковою, якщо у елементів буде
однаковою зміна об’єму
[3].
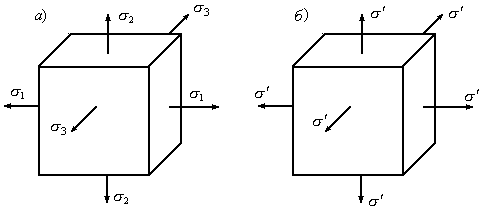
Рис.4.2
На
рис.4.2,а зображений елемент зі стороною,
що дорівнює одиниці (одиничний елемент),
навантажений різними за величиною
головними напруженнями. На рис.4.2,б
наведений допоміжний одиничний елемент,
на гранях якого діють однакові головні
напруження
![]() .
Для цього елемента відносна зміна об’єму
дорівнюватиме:
.
Для цього елемента відносна зміна об’єму
дорівнюватиме:
![]() ,
(4.9)
,
(4.9)
а повна питома енергія деформації визначається за формулою (4.3):
![]() . (4.10)
. (4.10)
Додатковий
елемент (Рис.4.2,б) при деформації змінює
тільки об’єм,
форма його залишається кубічною. Отже,
![]() =
0, з чого випливає, що:
=
0, з чого випливає, що:
![]() .
(4.11)
.
(4.11)
Величину
![]() визначимо з умови рівності відносних
змін об’ємів
обох елементів
визначимо з умови рівності відносних
змін об’ємів
обох елементів
![]() :
:
![]() .
(4.12)
.
(4.12)
Звідки
![]() .
.
Оскільки в обох елементах зміни об’ємів однакові, на підставі прийнятого припущення можна стверджувати, що
![]()
або
![]() .
(4.13)
.
(4.13)
Тепер з формули (4.8) можна знайти питому потенціальну енергію зміни форми:
![]() .
(4.14)
.
(4.14)
Підставляючи
у (4.14) значення
![]() та
та![]() з формул (4.3) і (4.13), після елементарних
перетворень остаточно одержуємо:
з формул (4.3) і (4.13), після елементарних
перетворень остаточно одержуємо:
![]() (4.15)
(4.15)
або
![]() . (4.16)
. (4.16)
Слід зазначити, що питома потенціальна енергія деформації грає значну роль при оцінці міцності конструкцій і деталей машин, які зазнають складного напруженого стану.
Приклад
4.1. Визначити відносні
лінійні деформації в головних напрямках,
відносну зміну об’єму
елементарного паралелепіпеда (Рис.4.3),
величину повної питомої потенціальної
енергії деформації, питому потенціальну
енергію зміни об’єму
і питому потенціальну енергію зміни
форми. Матеріал паралелепіпеда – сталь
з модулем пружності першого роду
![]() МПа
і коефіцієнтом Пуассона
МПа
і коефіцієнтом Пуассона![]() .
.

Рис.4.3
Розв’язок:
1.
Скористаємося результатами розв’язку
прикладу 3.3 з теми №3. Головні напруження
при вихідних нормальних і дотичних
напруженнях, чисельні значення яких
наведені на рис.4.3, у прикладі 3.3 були
отримані такими:
![]() МПа,
МПа,![]() МПа.
У цьому ж прикладі були визначені
напрямки головних напружень.
МПа.
У цьому ж прикладі були визначені
напрямки головних напружень.
2.
У розглянутому елементарному паралелепіпеді
має місце плоский напружений стан. З
огляду на те, що головне напруження
![]() ,
за формулою (3.73) знайдемо відносні
лінійні подовження:
,
за формулою (3.73) знайдемо відносні
лінійні подовження:
![]() ,
,
![]() ,
,
![]() .
.
3. Відносну зміну об’єму паралелепіпеда в результаті деформації знайдемо, скориставшись формулою (3.81):
![]() .
.
4.
В якості перевірки обчислимо відносну
зміну об’єму
елементарного паралелепіпеда за формулою
(3.82), з огляду на те, що головне напруження
![]() :
:
![]() .
.
Вийшло те саме число.
5.
Визначаємо повну питому потенціальну
енергію деформації, використовуючи
вираз (3.3), з огляду на рівність нулю
![]() :
:
![]()
=![]() 139195,84 Н/м2.
139195,84 Н/м2.
6.
Визначаємо питому потенціальну енергію
зміни об’єму
за формулою (4.13) за умови, що
![]() :
:
![]() Н/м2.
Н/м2.
7.
Визначаємо питому потенціальну енергію
зміни форми за формулою (4.16), з огляду
на те, що
![]() :
:
![]()
= 138662,5 Н/м2.
8. Виконуємо перевірку за формулою (4.8):
![]()
![]() Н/м2.
Н/м2.
Порівнюючи отриману суму з величиною повної питомої потенціальної енергії деформації, обчисленої в п.5 розглянутого прикладу, маємо зробити висновок, що значення для енергії практично збігаються.
