11.6. Матрична форма методу сил

При ручному розрахунку виникають значні обчислювальні ускладнення вже при ступеню статичної невизначуваності три і вище. Крім цього, зростає імовірність помилок при визначенні вантажних і одиничних переміщень, розв’язанні систем канонічних рівнянь та ін. З розвитком ЕОМ з'явилася можливість деякі рутинні і громіздкі обчислювальні операції перекласти на електронну машину. Однак ряд операцій, пов'язаних з підготовкою задачі, доводиться вирішувати вручну. Йдеться про побудову епюр вантажних і одиничних згинальних моментів. Чисельні значення вантажних і одиничних моментів, довжини ділянок, жорсткості елементів конструкції можна спеціальним чином обробити і занести в пам'ять ЕОМ. Усі подальші розрахунки ЕОМ виконує без участі людини за спеціально розробленою програмою. В результаті цих розрахунків ЕОМ друкує інформацію про розподіл внутрішніх силових факторів.

Сформулюємо матричний запис системи канонічних рівнянь. Для цього сформуємо кілька матриць, у число яких входять матриця-стовпець “зайвих” невідомих, матриця-стовпець вільних членів, матриця одиничних коефіцієнтів.

Матриця-стовпець “зайвих” невідомих , матриця-стовпець вільних членіві матриця одиничних коефіцієнтівмають відповідно вигляд:

; ;. (11.20)

Матричний запис системи канонічної системи рівнянь з урахуванням (11.20) має вигляд:

. (11.21)

Розв’язання матричного рівняння (11.21) відносно вектора “зайвих” невідомих набуває вигляду:

, (11.22)

де матрицю вільних членів можна визначити за допомогою матричного рівняння:

. (11.23)

Тут  матриця піддатливості. Для  го елемента системи матриця піддатливості має вигляд:

. (11.24)

Матрицю одиничних коефіцієнтів знайдемо з матричного рівняння:

. (11.25)

З урахуванням (11.23) і (11.24) матрична форма системи канонічних рівнянь має вигляд:

. (11.26)

Матричне рівняння для визначення сумарних згинальних моментів записується у вигляді:

(11.27)

Сформулюємо порядок розв’язання статично невизначуваних систем методом сил матричним способом:

1. Розбиваємо статично невизначувану систему на ділянки (Рис.11.32), вибираємо точку спостереження, вводимо додатні і від’ємні сторони і проставляємо зліва направо “характерні” перерізи на кожній ділянці.

2. Визначаємо ступінь статичної невизначуваності системи.

3. Вибираємо основну систему.

4. Зображуємо еквівалентну систему.

5. Будуємо епюри вантажних моментів .

Рис.11.32.

6. Зображуємо одиничні стани системи і будуємо епюри одиничних моментів .

7. Формуємо матрицю вантажних моментів:

, (11.28)

де  кількість ділянок

8. Формуємо матриці одиничних моментів:

. (11.29)

9. Формуємо матрицю піддатливості :

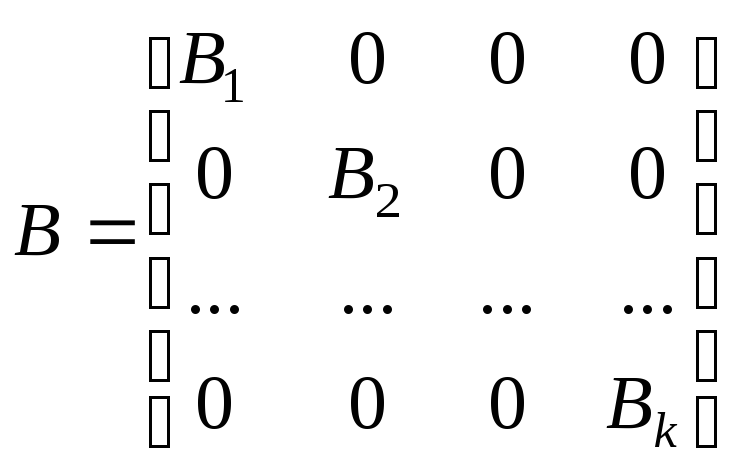, (11.30)

де  тий елемент матриці піддатливості , визначається з виразу (11.24).

10. Вводимо сформовані матриці у визначеній послідовності у пам'ять ЕОМ. ЕОМ обчислює значення всіх “зайвих” невідомих, сумарних згинальних моментів і поперечних силу кожному з “характерних” перерізів і друкує у вигляді відповідних векторів. Друкується також вся вихідна інформація.

11. Використовуючи дані ЕОМ про вектори і, будуємо відповідні сумарні епюри.

12. Методом вирізання вузлів будуємо епюру поздовжніх сил .

11.7. Особливості розрахунку статично невизначуваних (нерозрізних) балок методом сил

Розглянемо нерозрізну балку (Рис.11.33). Балка навантажена зосередженою силою і має чотири опори: крайня ліва опора жорстка, три інші опори шарнірно рухомі. Ступінь статичної невизначуваності балки дорівнюєі може бути визначена з формули (11.3).

Рис.11.33

Розв’язуючи цю задачу в традиційному плані, було б природним відкинути зайві зв'язки, взявши в якості “зайвих” невідомі реакції в цих зв'язках ,і. Однак, традиційне розв’язання задачі шляхом відкидання зовнішніх зв'язків виявляється при розрахунку нерозрізних балок досить громіздким. У зв'язку з цим зазвичай такі задачі розв’язують шляхом врізання шарнірів у тіло балки таким чином, щоб при цьому балка стала статично визначуваною і залишалася геометрично незмінюваною. Варіант основної системи в такій постановці наведений на рис.11.34.

Рис.11.34.

Шарніри можна врізувати в будь-якому місці балки за умови її геометричної незмінюваності. Але простіше врізувати шарніри на проміжних опорах. В результаті ми отримуємо статично визначувану (розрізну) балку, що складається з декількох незалежних одна від одної балок. В якості “зайвих” невідомих при цьому приймаються внутрішні опорні моменти. Вигляд еквівалентної системи наводиться на рис.11.35.

Зміст канонічних рівнянь методу сил при такому виборі основної системи принципово змінюється. Якщо в колишній постановці ідея методу сил складалася у визначенні переміщень у місці відкинутих зв'язків і прирівнюванні цих переміщень нулю, то при розрахунку нерозрізних балок такий підхід не годиться.

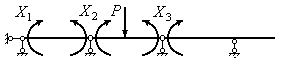
Рис.11.35

Виходячи з енергетичної природи методу Мора, момент може виконувати роботу тільки на куті повороту перерізу. Але кути повороту перерізів, у яких прикладені опорні моменти, крім крайнього лівого, в процесі деформації балки не дорівнюють нулю. А от взаємний кут повороту двох прилягаючих до опори перерізів на опорі, де був врізаний шарнір, дорівнє нулю (Рис.11.3,б).

Рис.11.36

У цьому і є фізичний зміст системи канонічних рівнянь методу сил при розрахунку нерозрізних балок.