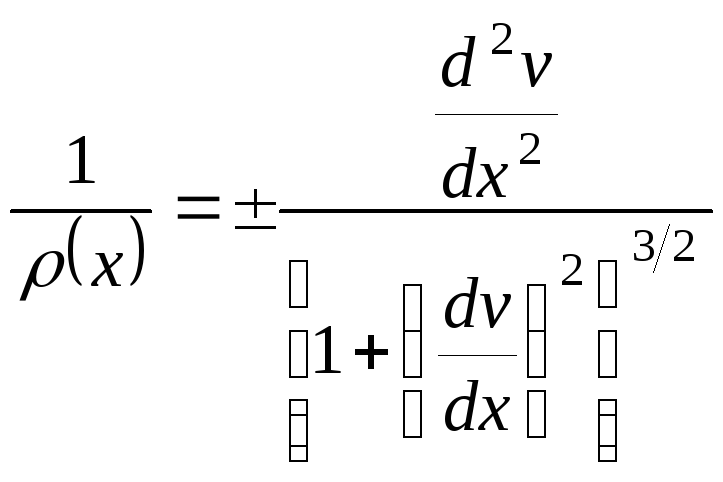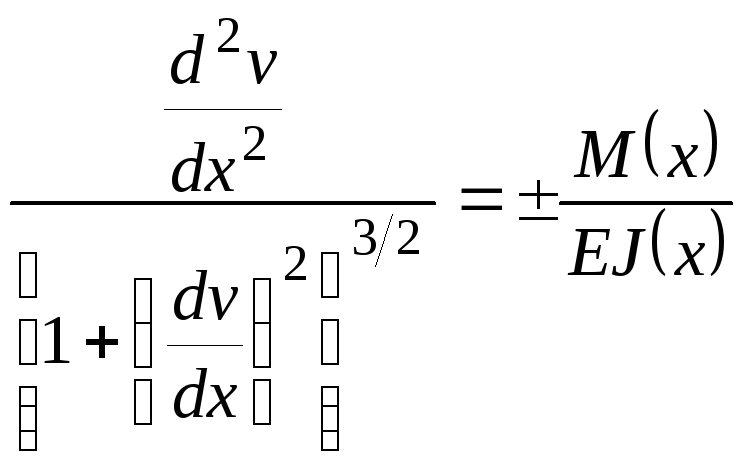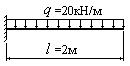Подставляем координату сечения с в уравнение (б). Получим:
.
После подстановки численного значения жесткости поперечного сечения балки в выражение для угла поворота, имеем:
рад
.
Знак “+” у угла поворота означает, что поворот сечения происходит по часовой стрелке. Это верно, так как решение задача выполнялось в левой системе координат.
Пример
6.11. Определить
номер прокатного профиля из условия
жесткости для балки, изображенной на
рис.6.15. Материал балки – сталь с модулем
упругости
МПа.
Допускаемый прогиб составляет
,
где
м
– пролет балки. Допускаемое напряжения
для материала балки
МПа.
Решение:
1. Определяем опорные реакции. Для этого составим два уравнения равновесия:
;
(а);
.
(б)
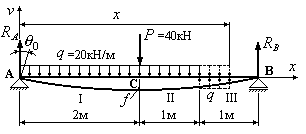
Рис.6.15
Решая
уравнения (а) и (б) относительно реакций,
находим:
кН,
кН.
2.
Начало координат выбираем на левом
конце балки. Ось прогибов
направляем вверх, ось
вправо.
3.
Определяем начальные параметры. Из двух
начальных параметров прогиб в начале
координат
;
угол поворота
найдем, приравняв нулю прогиб на опоре
В при
м:
.
(в)
Решая
уравнение (в) относительно
,
находим:
.
(г)
4.
Определяем прогиб посредине балки в
сечении С. Будем считать, что максимальный
прогиб
(стрела
прогиба) возникает посредине пролета.
Сечение С принадлежит первому участку,
поэтому из универсального уравнения
упругой линии, вычеркивая члены, не
принадлежащие первому участку, получим
при
м:
.
5. Находим требуемый момент инерции сечения из условия жесткости:
.
(д)
Допускаемый
прогиб
м.
Подставляя в условие жесткости (д) модуль
стрелы прогиба и величину допускаемого
прогиба, получаем:
.
Откуда
м4
см4.
Из
сортамента прокатной стали подбираем
номер прокатного двутавра. Таким
двутавром оказался двутавр № 40 с
моментом инерции
см4
и моментом сопротивления
см3.
6.
Выполняем проверку выбранного двутавра
на прочность. Максимальный изгибающий
момент, действующий в балке, равен
кНм
(расчет максимального изгибающего
момента здесь не приводится). Подставляем
в условие прочности значения максимального
изгибающего момента
и осевого момента сопротивления
и находим максимальное напряжение,
действующее в балке:
МПа.
Этот
напряжение оказалось меньше допускаемого
МПа.
Таким образом, окончательно принимаем двутавр №40, удовлетворящий как условию прочности, так и условию жесткости.
6.5.Тесты к теме №6 “Определения перемещений при изгибе. Расчет балок на жесткость”
|
№ |
Вопрос |
Время на ответ, сек |
|
1 |
Что мы называем жесткостью детали машин или конструкции? |
30 |
|
|
1. Способностью сопротивляться внешним нагрузкам, не разрушаясь? |
|
|
|
2. Способностью сопротивляться внешним нагрузкам без видимых деформаций? |
|
|
|
3. Способность сопротивляться большим деформациям при малом изменении нагрузки? |
|
|
|
4. Способность деформироваться без нарушения прочности? |
|
|
2 |
Что называется деформацией тела? |
30 |
|
|
1. Изменение положения тела в пространстве? |
|
|
|
2. Изменение теплопроводности тела? |
|
|
|
3. Изменение стоимости тела? |
|
|
|
4. Изменение формы и размеров тела? |
|
|
3 |
Какое из перемещений поперечных сечений не возникает при плоском изгибе балки? |
30 |
|
|
1. Прогиб. |
|
|
|
2. Угол поворота. |
|
|
|
3. Угол закручивания. |
|
|
|
4. Продольное перемещение. |
|
|
4 |
Первая производная от прогиба по продольной координате есть: |
30 |
|
|
1. Синус угла поворота сечения? |
|
|
|
2. Тангенс угла поворота сечения? |
|
|
|
3.Косинус угла поворота сечения? |
|
|
|
2. Котангенс угла поворота сечения? |
|
|
5 |
Каким из уравнений описывается изогнутая ось балки при плоском поперечном изгибе? |
30 |
|
|
1. Алгебраическим. |
|
|
|
2. Интегральным. |
|
|
|
3. Дифференциальным. |
|
|
|
4. Тригонометрическим. |
|
|
6 |
Какое из уравнений является приближенным (основным) уравнением упругой линии балки? |
30 |
|
|
1.
|
|
|
|
2.
|
|
|
|
3.
|
|
|
|
4.
|
|
|
7 |
При определении перемещений при плоском изгибе как поступают с основным дифференциальным уравнением упругой линии? |
30 |
|
|
1. Дифференцируют. |
|
|
|
2. Раскладывают в ряд. |
|
|
|
3. Интегрируют. |
|
|
|
4. Потенцируют. |
|
|
8 |
Сколько раз нужно проинтегрировать основное дифференциальное уравнение упругой линии, чтобы получить выражение для прогиба ? |
|
|
|
1. Два раза. |
|
|
|
2. Три раза. |
|
|
|
3. Один раз. |
|
|
|
4. Четыре раза |
|
|
9 |
Сколько раз нужно проинтегрировать основное дифференциальное уравнение упругой линии, чтобы получить выражение для угла поворота ? |
|
|
|
1. Два раза. |
|
|
|
2. Три раза. |
|
|
|
3. Один раз. |
|
|
|
4. Четыре раза |
|
|
10 |
Что
из себя представляет уравнение
|
30 |
|
|
1.
Выражение для изгибающего момента
|
|
|
|
2.
Выражение для поперечной силы
|
|
|
|
3.
Выражение для угла поворота
|
|
|
|
4.
Выражение для интенсивности
распределенной нагрузки
|
|
|
|
5.
Выражение для прогиба
|
|
|
11 |
Что
из себя представляет уравнение
|
30 |
|
|
1.
Выражение для изгибающего момента
|
|
|
|
2.
Выражение для поперечной силы
|
|
|
|
3.
Выражение для угла поворота
|
|
|
|
4.
Выражение для интенсивности
распределенной нагрузки
|
|
|
|
5.
Выражение для прогиба
|
|
|
12 |
Что
из себя представляет уравнение
|
30 |
|
|
1.
Выражение для изгибающего момента
|
|
|
|
2.
Выражение для поперечной силы
|
|
|
|
3.
Выражение для угла поворота
|
|
|
|
4.
Выражение для интенсивности
распределенной нагрузки
|
|
|
|
5.
Выражение для прогиба
|
|
|
13 |
Что можно определить с помощью выражения
|
30 |
|
|
1.
Поперечную силу
|
|
|
|
2.
Прогиб
|
|
|
|
3.
Интенсивность распределенной нагрузки
|
|
|
|
4.
Угол поворота
|
|
|
|
5.
Изгибающий момент
|
|
|
14 |
Что можно определить с помощью выражения
|
60 |
|
|
1.
Поперечную силу
|
|
|
|
2.
Прогиб
|
|
|
|
3.
Интенсивность распределенной нагрузки
|
|
|
|
4.
Угол поворота
|
|
|
|
5.
Изгибающий момент
|
|
|
15 |
При интегрировании основного дифференциального уравнения упругой линии используют граничные условия. С какой целью? |
|
|
|
1.
Для определения границ изменения
величины изгибающего момента
|
|
|
|
2.
Для определения границ изменения
величины поперечной силы
|
|
|
|
3.
Для определения границ изменения
величины угла поворота
|
|
|
|
4.
Для определения границ изменения
величины прогиба.
|
|
|
|
5.
Для определения значений постоянных
интегрирования.
|
|
|
16 |
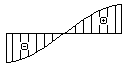
Какая из эпюр углов поворота соответствует предстваленной на рисунке эпюре изменения прогибов?
|
120 |
|
|
1.
|
|
|
|
2.
|
|
|
|
3.
|
|
|
|
4.
|
|
|
17 |
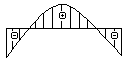
Какая из эпюр прогибов соответствует представленной на рисунке эпюре изгибающих моментов?
|
120 |
|
|
1.
|
|
|
|
2.
|
|
|
|
3.
|
|
|
|
4.
|
|
|
18 |
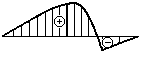
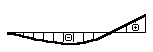
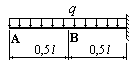
В сколько раз прогиб в сечении А на конце изображенной на рисунке балки, больше, чем прогиб в сечении В посредине балки?
|
240 |
|
|
1. В 3 раза. |
|
|
|
2. В 3,5 раза. |
|
|
|
3. В 2,8 раза. |
|
|
|
4. В 3,2 раза. |
|
|
19 |
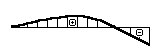
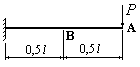
В сколько раз угол поворота сечения А на конце изображенной на рисунке балки больше, чем угол поворота сечения В посредине балки?
|
300 |
|
|
1. В 1,225 раза. |
|
|
|
2. В 1,143 раза. |
|
|
|
3. В 1,159 раза. |
|
|
|
4. В 1,137 раза. |
|
|
20 |
Найти
стрелу прогиба (в мм) балки, изображенной
на рисунке, если жесткость поперечного
сечения балки равна
|
240 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
?
.
.
.
.
?
.
.
.
.
.
.
.
.
,
.
кНм2.