Подставляя в эти уравнение , получим:

;(6.22)

.(6.23)

Таким образом, произвольные постоянные иравны соответственно углу поворота и прогибу в начале координати, которые принято называтьгеометрическими начальными параметрами. Подставляя в уравнение (6.15) вместо постоянных интегрированияиравные им значения начальных параметров, получаем:

. (6.24)

Если на балку действует несколько моментов и сил, а также несколько участков распределенной нагрузки, уравнение для прогибов можно составить в следующем виде:

(6.25)

Уравнение (6.25) обычно называют универсальным уравнением упругой линии.

Продифференцировав уравнение (6.25), получим уравнение углов поворота сечения:

. (6.26)

Здесь и в формуле (6.25) приняты следующие обозначения:  тип внешнего силового фактора (); показатель степени, получаемый при интегрировании дифференциального уравнения упругой линии;  координата сечения, в котором приложена сросредоточенная сила или момент, или координата сечения, к котором начинается действие распределенной нагрузки. Соответствие величины показателя степени типу внешнего фактора приведено в таблице 6.1.

Таблица 6.1

Тип внешней нагрузки	Показатель степени
Внешний момент	2
Сосредоточенная сила	3
Интенсивность распределенной нагрузки	4

Знаки слагаемых в уравнения (6.25) и (6.26) определяются знаком изгибающего момента, который вызывается соответствующим силовым фактором.

Характерной особенностью метода начальных параметров является то, что для определения перемещения нет необходимости составлять и интегрировать дифференциальное изогнутой оси балки. Достаточно составить универсальное уравнение упругой линии (6.25), из условий на опорах найти начальные параметры и снова воспользоваться универсальным уравнением, чтобы найти прогиб в рассматриваемом сечении.

Рассмотрим пример определения перемещений по методу начальных параметров.

Пример 6.10. Определить прогиб посредине пролета балки, приведенной на рис.6.14, и угол поворота сечения С на левом конце балки. Материал балки  сталь с модулем упругости МПа. Балка представляет собой двутавр № 20 с моментом инерциисм⁴.

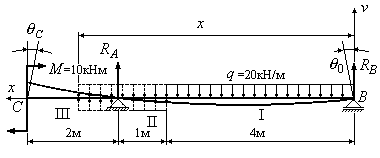
Решение:

1. Определим опорные реакции. Для этого составим два уравнения равновесия:

. Откуда кН;

. Откуда кН.

2. Помещаем начало координат на правом конце балки в точку В, ось прогибов направляем вверх, ось влево. Чем в данном случае определен выбор начала координат? Если выбрать начало координат на левом конце балки в сечении С, то предварительно придется искать оба начальных параметра, так как ни угол поворота сечения С, ни прогиб в этом сечении заранее неизвестны. Для их определения потребуется составлять систему из двух уравнений и решать ее относительно двух неизвестных начальных параметров. Если же выбрать начало координат на правом конце балки в сечении В, то находить придется лишь один начальный параметр – угол поворота сечения В . Второй начальный параметр – прогиб в сечении В– искать не нужно, так как он равен нулю из граничного условия на опоре В.

3. Разбиваем балку на участки (Рис.6.14) и записываем универсальное уравнение упругой линии (6.25) для последнего участка:

(а)

4. Из уравнения (а) определяем начальный параметр из условия, что прогиб в сечении А прим равен нулю:

.

Откуда

.

5. Определяем прогиб посредине пролета балки при м. Так как сечение посредине балки принадлежит первому участку, вычеркиваем из универсального уравнения все члены, принадлежащие второму и третьему участкам. Получим:

.

Подставляем численные значения модуля упругости и момента инерции в полученное выражение. Получаем:

м = 44,3мм.

Знак “” означает, что направление прогиба не совпадает с направлением оси прогибов .

6. Определяем угол поворота сечения С. Для этого воспользуемся выражением (6.26). Так как сечение С принадлежит третьему участку, составим уравнение для угла поворота для этого участка:

. (б)