6.3. Дифференциальные зависимости при изгибе

Ранее были получены дифференциальные зависимости между интенсивностью распределенной нагрузки , поперечной силойи изгибающим моментом:

; ;. (6.8)

Кроме того, были получены дифференциальные зависимости между прогибом и углом поворота, прогибом и изгибающим моментом, углом поворота сечения и изгибающим моментом:

; ;. (6.9)

Эти зависимости, после некоторого преобразования, можно расположить последовательно: (6.10)

Из этих уравнений видно, что, зная нагрузку и устройство опор балки, можно последовательным интегрированием получить величины,,,. С другой стороны, зная уравнение упругой линии, можно путем последовательного дифференцирования поиз функцииполучить,,и. Для графического изображения этих зависимостей условимся положительные значения всех перечисленных величин откладывать вверх, а отрицательные – вниз; положительное направление осив правой системе координат примем вправо, поворот сечения по часовой стрелке – отрицательным, а против – положительным. В левой системе координат – наоборот.

Приведем несколько примеров построения эпюр распределения поперечных сил, изгибающих моментов, углов поворота сечений и прогибов.

Пример 6.6. Построить качественные эпюры распределение поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, для балки, изображенной на рис. 6.8.

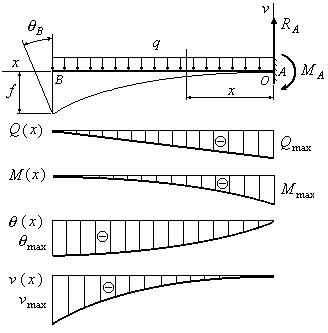
Рис.6.8

Пример 6.7. Построить качественные эпюры распределения поперечных сил, изгибающих моментов, углов поворота сечений и прогибов, для балки, изображенной на рис. 6.9.

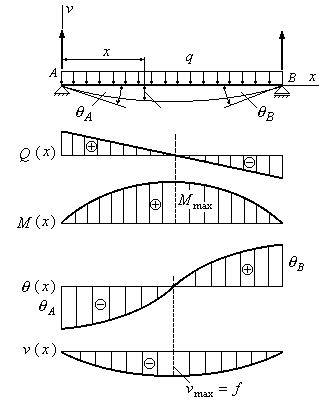
Рис.6.9

При построении эпюр углов поворота и прогибов следует придерживаться некоторых правил. Сформулируем их:

1. Так как представляет собой диаграмму производной от эпюры углов поворота, то ординаты эпюрыпропорциональны тангенсу угла наклона касательной к эпюре. В сечениях, где, касательная к кривойдолжна быть параллельна оси абсцисс (Рис.6.8 сечение А и 6.9  сечения А и В). Скачку на эпюре моментов соответствует угловая точка на эпюре (Рис.6.8 – сечение А и 6.10 – сечение С).

2. Вторая производная прогиба

имеет знак момента. Если момент положителен (сжаты верхние волокна), то вогнутость на эпюре будет обращена в сторону положительных прогибов(вверх). При отрицательном моменте вогнутость пораболы обращена вниз. Так как ординаты эпюр изгибающих моментов мы условились откладывать со стороны сжатых волокон, то вогнутость эпюры прогибоввсегда обращена в ту сторону, с которой расположены ординаты эпюры изгибающих моментов.

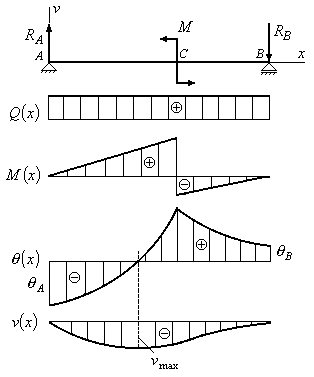
Рис.6.10

3. Вторая производная угла поворота

имеет знак поперечной силы. Если положительна, то выпуклость на эпюребудет обращена вниз (Рис.6.8, 6.9). Привыпуклость направлена в сторону оси, т.е. вверх (Рис.6.9). В сечении, гдеменяет знак, на эпюренаблюдается точка перегиба. (Рис.6.9).

4. Если изгибающий момент равен нулю напротяжении какого-либо участка балки, то на этом участке угол поворота не меняется, а прогиб меняется по линейной зависимости.

5. На тех участках балки, где эпюра изменяется по линейному закону, эпюраменяется по закону квадратной параболы, а эпюра по закону параболы третьего порядка. Там, где эпюра изменяется по закону квадратной параболы, эпюраменяется по закону параболы третьего порядка, а эпюра по закону параболы четвертого порядка.

6. На участках, где действует постоянный момент, эпюра меняется по линейному закону, а эпюра прогибов меняется по закону квадратной параболы.

7. Так как представляет собой график изменения по длине балки тангенсов наклона касательных к упругой линии, то можно утверждать следующее:

а) на участках, где в направлении оси прогибвозрастает, угол наклонабудет положителен. Наоборот, при уменьшенииуглы наклонабудут отрицательны (Рис.6.10, участок АС);

б) в сечениях, где , касательная к эпюрегоризонтальна, т.е. в этом сечении на эпюренаблюдается аналитический максимум или минимум (Рис.6.9).

Рассмотрим еще несколько примеров построения эпюр углов поворота и прогибов.

Пример 6.8. Какая из эпюр углов поворота соответствует приведенной на рис.6.11 эпюре изменения прогибов, представляющей собой параболу четвертого порядка?

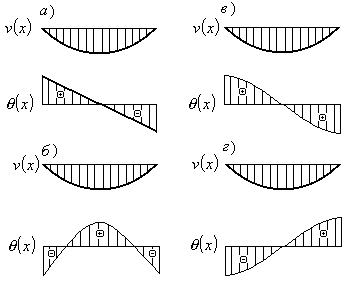
Решение:

Вариант а) отпадает, так как эпюра углов поворота может меняться по линейному закону лишь в том случае, если эпюра прогибовпредставляет собой квадратную параболу.

Вариант б) не подходит по той причине, что максимального значения прогиб достигает в сечении, в котором угол поворота равен нулю. Такого соответствия в этом варианте нет.

Вариант в) не подходит, так как на левой части эпюры прогиб убывает слева направо при положительном тангенсе угла наклона касательной к кривой прогибов. В этом варианте нет соответствия между знаком приращения прогиба и знаком эпюры углов поворота.

Вариант г) подходит по ряду признаков: во-первых, совпадают знаки приращения прогиба и знаки угла поворота на всей длине участка. Во-вторых, экстремального значения прогиб достигает в сечении, в котором угол поворота равен нулю. В-третьих, в сечениях на левом и правом концах участка, там, где прогиб равен нулю, касательная к кривой углов поворота параллельна базисной линии, что соответствует равенству нулю тангенса угла поворота в этих сечениях.

Таким образом, из четырех вариантов эпюра изменения углов поворота соответствует эпюре изменения прогибов в последнем варианте.

Пример 6.9.Какая из эпюр прогибов соответствует представленной на рис.6.12 эпюре изгибающих моментов, если положительное направление оси направлено вверх?

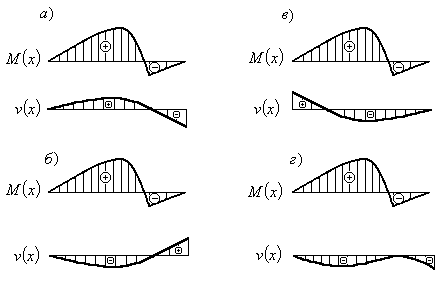
Рис.6.12

Решение:

Вариант а) не подходит, так как положительному изгибающему моменту в выбранной ситеме координат должна соответсвовать положительная кривизна упругой линии балки. Такого соответствия здесь нет.

Вариант б) не подходит по той причине, что изогнутая ось балки имеет кривизну одного и того же знака на всей длине участка, в то время как изгибающий момент меняет знак по длине участка.

Вариант в) не подходит по той же причине.

Вариант г) подходит, так как имеет место соответствие знаков изгибающего момента и знаков кривизны изогнутой оси на соответствующих участках.