14.7. Тесты к теме №14 “Устойчивость сжатых стержней”

№

Вопрос

Время на ответ, сек

1

Что называется устойчивостью сжатого стержня?

30

1.Способность сопротивляться нагрузкам без видимих деформаций.

2.Способность сопротивляться нагрузкам, не разрушаясь.

3. Способность сопротивляться большим деформациям при малом изменении сжимающей силы.

4. Способность сопротивляться малым деформациям при малом изменении сжимающей силы.

2

Какая сила называется критической?

30

1. Наибольшая сжимающая сила, при которой стержень теряет устойчивость.

2. Наименьшая сжимающая сила, при которой стержень теряет устойчивость.

3. Наибольшая растягивающая сила, при которой стержень теряет устойчивость.

4. Наименьшая растягивающая сила, при которой стержень теряет устойчивость.

3

Какая форма упругого равновесия называется критической?

30

1. Безразличная.

2. Устойчивая.

3. Неустойчивая.

4. Безусловная.

4

Если  критическая сила, а  коэффициент запаса устойчивости, то каким из выражений следует воспользоваться для определения величины допускаемой сжимающей силы?

30

1.

2.

3.

4.

5

Какой вид деформации должен возникнуть в конструкции, чтобы она потеряла устойчивость?

20

1. Кручение.

2. Сжатие.

3. Изгиб.

4. Растяжение.

6

При увеличении критических напряжений устойчивость стержня

20

1. Увеличивается?

2. Уменьшается?

3. Не изменяется?

7

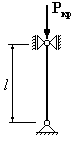
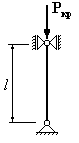
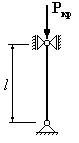
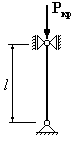
Для которого из приведенных на рисунке стержней коэффициент свободной (приведенной) длины ?

1. 2. 3. 4.

20

8

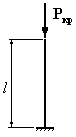
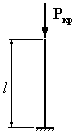
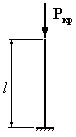
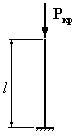
Для которого из приведенных на рисунке стержней коэффициент свободной (приведенной) длины ?

1. 2. 3. 4.

20

9

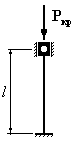
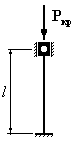
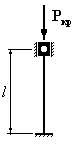
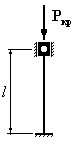
Для которого из приведенных на рисунке стержней коэффициент свободной (приведенной) длины ?

1. 2. 3. 4.

20

10

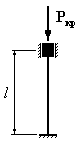
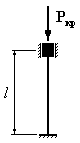
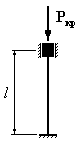
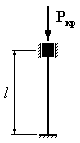
Для которого из приведенных на рисунке стержней коэффициент свободной (приведенной) длины ?

1. 2. 3. 4.

20

11

Используя формулу Эйлера, определить величину критической силы (в кН) для стального стержня с шарнирным опиранием концов. Поперечное сечение стержня – круг диаметром см. Длина стержня 4 м. Результат округлить до ближайшего целого значения.

300

12

Используя формулу Ясинского, определить величину критической силы (в кН) для стального стержня с шарнирным опиранием концов. Поперечное сечение стержня – круг диаметром см. Длина стержня 1м. Значения коэффициентов в формуле Ясинского принять:МПа,МПа. Результат округлить до ближайшего целого значения.

300

13

Какой из трех стержней одинаковой длины и одинаковыми условиями закрепления концов имеет большую критическую силу? (См. рисунок). Площадь поперечных сечений стержней одинакова и равняется см².

240

14

Чем определяются пределы применения формулы Эйлера?

1. Уровнем допускаемых напряжений.

2. Величиной деформации.

3. Минимальной величиной осевого момента инерции.

4. Предельным значением гибкости.

15

Определить наименьшую гибкость стержня, при которой для вычислении критической силы еше применяется формула Эйлера, если стержень изготовлен из стали с пределом пропорциональности МПа и модулем упругостиМПа.

240

16

Который из двух стержней одинаковой длины и с одинаковой площадью поперечного сечения, условия закрепления закрепления которых и нагрузка одинаковы, является более гибким – стержень квадратного или круглого сечения?

240

1. Гибкость стержня с круглым поперечным сечением больше.

2. Гибкость стержня с квадратным поперечным сечением больше.

3. Гибкости обоих стержней одинаковы.

17

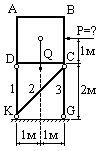
Водонапорный бак АВСD весом кН поддерживается стержнями DK, CK, CG и подвергается действию ветровой нагрузки Р. В узлах C, D, K, G крепление стержней является шарнирным. Поперечные сечения всех стержней одинаковы. При каком наименьшем значении нагрузки Р (в кН) стержень №3 не следует проверять на устойчивость?

180

18

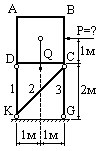
Водонапорный бак АВСD весом кН поддерживается стержнями DK, CK, CG и подвергается действию ветровой нагрузки Р. Поперечные сечения всех стержней одинаковы. При каком значении нагрузки Р (в кН) стержень №2 не следует проверять на устойчивость?

180

19

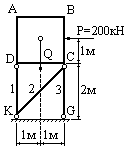
Водонапорный бак АВСD весом кН поддерживается стержнями DK, CK, CG и подвергается действию ветровой нагрузкикН. определить площадь поперечного сечения стержня №1 (в см²). Принять МПа, коэффициент продольного изгиба.

180

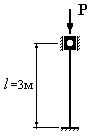
20

Определить величину допускаемой силы Р для стержня (в кН), приведенного на рисунке. Площадь поперечного сечения стержня – круг диаметром см. Принять для гибкости стержнязначение коэффициента продольного изгиба, длякоэффициент,МПа. Результат решения округлить до целого числа.

300

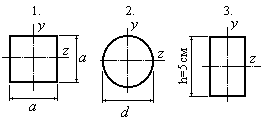
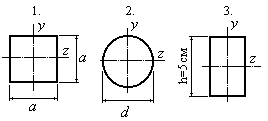
21

Какое из приведенных на рисунке поперечных сечений сжатых стержней, условия нагрузки и условия закрепления концов которых одинаковы, будет более устойчивым, если площади поперечных сечений у всех стержней одинаковы и равняются см²?

240

22

Какая из физических характеристик влияет на рациональный выбор материала сжатого стержня при потере устойчивости?

30

1. Предел пропорциональности.

2. Модуль упругости.

3. Коэффициент Пуассона.

4. Предел прочности.

23

Каким из приведенных ниже выражений следует воспользоваться для определения рациональности выбора формы поперечного сечения сжатых стержней, теряющих устойчивость?

30

1.

2.

3.