6. ВИЗНАЧЕНИЙ ІНТЕГРАЛ
Література: [1, розділ 8, п. 8.2, 8.3]; [3, розділ 6, п. 6.2]; [5, глава 10, § 1-5]; [8, розділ 2, п. 2.1-2.7]; [11, розділ 2, п. 2.1-2.7]; [13, розділ 7, § 23, 24]; [4, розділ 4, глава 11, п. 11.1-11.6]; [15, розділ 5, § 1-4]; [17, розділ 9].
Індивідуальне завдання 6.1
6.1.ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА ДЛЯ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ГЕОМЕТРІЇ
Узадачах 1, 2 обчислити площу фігури, обмеженої вказаними лі-
ніями.
Задача 1
1. |
y = x2 , y2 = x. |
||
3. |
y = |
|
, y = x3. |
x |
|||
5. |
x2 = 2 py, y2 = 2 px. |
||
7. |
y = ln x, x = e, x = e2 , y = 0. |
||
9.y = 2x - x2 , y = -x.
11.y = ex , y = e-x , x =1.
13. |
y =1/(1 + x2 ), |
y = x2 / 2. |
|
||
15. |
y2 |
= x3 , x = 0, y = 4. |
|
||
17. |
y = 2x + x2 , y = x + 2. |
|
|||
19. |
y = 4 - (x -1) |
2 , y = 3x / 2, |
x = 0. |
||
21. |
y2 |
= x3 , x = 2. |
|
|
|
23. |
y2 |
= (4 - x3 ), |
x = 0. |
|
|
25. |
y = x3 , y =1, |
x = 0. |
|
||
27. |
y = 2x , y = 2x - x2 , |
x = 0, |
x = 2. |
||
29. |
y = arcsin x, x = 0, |
x = p / 4. |
|||
2.y = x2 , y = 3 - x.
4.y = 
x, x + y = 2, y = 0.
6.y = 2 - x2 , y3 = x2 .
8. y = x2 , y = 3 - 2x.
10. |
y = x2 , |
y = x2 / 2, y = 2x. |
12. |
xy = 2, |
y = 2x, y = x / 2. |
14.y2 = x +1, y 2 = 9 - x.
16.y = x2 / 4, y = 3x - x2 / 2.
18.y2 = 9x, y = 3x.
20.y2 = 4x, x2 = 4 y.
22.y = x2 , y = 2 - x2 .
24.y = 4 - x2 , 3x - 2 y = 6.
26. |
xy = 6, x + y - 7 = 0. |
|
28. |
x2 = 4 y, |
y = 8 /(x2 + 4). |
30. |
y = x +1, |
y = cos x, y = 0. |
ДВНЗ “Українська академія банківської справи НБУ”
62
|
|
|
|
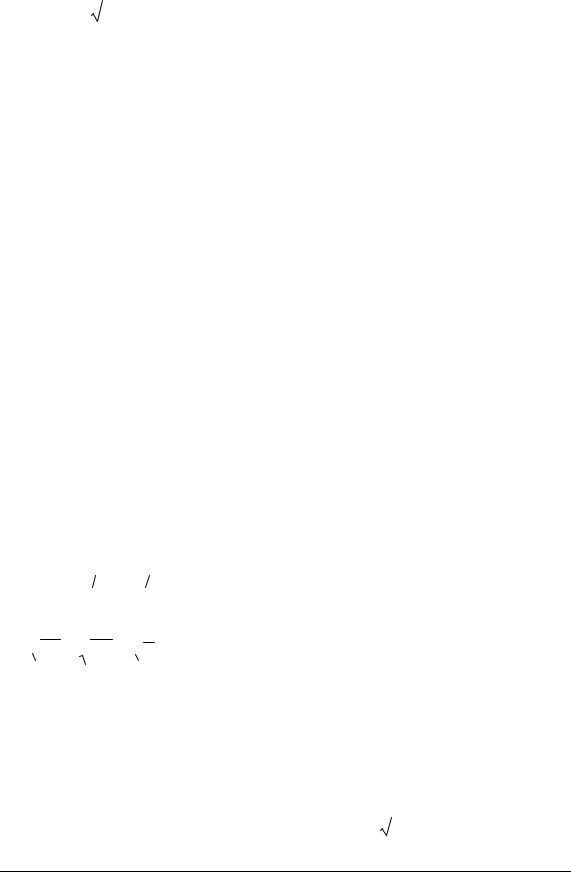
Задача 2 |
1. |
r = 3 |
|
. |
|
cos 2j |
||||
3. |
r 2 = a2 cos 2j. |
|||
5. |
r = 4 cos 3j. |
|
|
|
7. |
r = 2(1 - cosj). |
|||
9. |
x = 4(t - sin t), y = 4(1 - cos t). |
|||
11. |
r = 2sin 3j. |
|
|
|
13. |
r = 2cos 4j. |
|
|
|
15. |
x = 2cos3 t, |
|
y = 4sin3 t. |
|
17. |
х = 3cos t, y = 2sin t. |
|||
19. |
x = 2 cos3 t, |
|
y = 2sin3 t. |
|
21. |
r = a sin kj. |
|
|
|
23. |
r = 2cosj. |
|
|
|
25. |
r = 4cosj, |
r = 2cosj. |
||
27. |
r = 2cosj, |
r = 2sin j. |
||
29. |
íìx = 3(cost + t sin t), |
|||
|
î y = 3(sin t - t cost) |
|||
|
(0 £ t £ p ), |
|
y = 0. |
|
Задача 3
Обчислити довжину дуги лінії.
2. |
r = aj, 0 £ j £ 2p. |
4. |
x = 7 cos3 t, y = 7 sin 3 t. |
6. |
r = 3cos 2j. |
8.r2 = 2sin 2j.
10.r = 2(1 + cosj).
12. |
r = 2 + cosj. |
14. |
r = 2sin 5j. |
16. |
r = 4sin 2 j. |
18. |
r = 2cos 5j. |
20. |
r = a sin kj. |
22. |
r = 4sinj. |
24. |
r = 3sin 4j. |
26. |
r = 2 + sinj. |
28. |
r = 4cos 3j, r ³ 2. |
30.ìíx = a(2 cost - cos 2t), î y = a(2sin t - sin 2t)
(0 £ t £ p ), y = 0.
1. |
x = 2 cos3 t, y = 2 sin3 t. |
||
2. |
x = 2(cos t + t sin t), y = 2(sin t - t cos t) (0 £ t £ p ). |
||
3. y = |
a |
(ex a + e-x a ) (0 £ x £ a). |
|
|
|||
|
2 |
|
|
4. |
y = ln sin x від x = π/3 до x = π/2. |
||
5. 3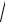
x2 + 3
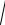y2 = 3
9. 6. x2
3 + y2
3 = 42
3.
7. y2 = (x +1)3 , x = 4.
8. |
y =1 - ln cos x (0 £ x £ p / 6). |
|||
9. |
r = 6 cos3 (j / 3) (0 £ j £ p / 2). |
|||
10. |
x = 4 cos3 t, |
y = 4 sin3 t. |
||
11. |
y2 = (x -1)3 |
від точки А(1; 0) до точки В(6; |
|
). |
125 |
||||
ДВНЗ “Українська академія банківської справи НБУ”
63
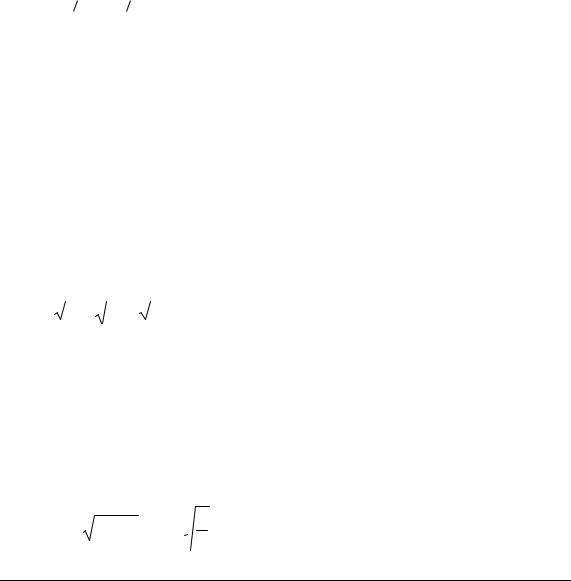
12.y2 = x3, що відтинається прямою x = 5.
13.r = 3cosj.
14.r = 3(1 - cosj).
15.y = ln x від точки А(1; 0) до точки В(e; 1).
16. x = 5 cos2 t, y = 5 sin 2 t (0 £ t £ p / 2).
17.9 y2 = 4(3 - x)3 між точками перетину з віссю Oy.
18.r = 3sin j.
19.y = ln sin x (p / 3 £ x £ p / 2).
20. x = 9(t - sin t), y = 9(1 - cos t) (0 £ t £ 2p ).
21.r = 2(1 - cosj).
22.y2 = (x -1)3 від точки А(2; –1) до точки В(5; –8).
23. |
x = 7(t - sin t), |
y = 7(1 - cos t) (2p £ t £ 4p ). |
|
24. |
y = ex 2 + e- x 2 |
(0 £ x £ 2). |
|
25. |
x = 4 cos3 t, |
y = 4 sin3 t. |
|
26. x = et cos t, |
y = et sin t від t = 0 до t = 1. |
||
27.r = 5sin j.
28.r = 4 cosj.
29.r = 5(1 + cosj).
30.y2 = x3 від точки А(0; 0) до точки В(4; 8).
Задача 4
Обчислити об’єм тіла, отриманого обертанням плоскої фігуриФ навколо вказаної осі координат.
1. Ф: |
y2 = 4 - x, x = 0, Oy. |
|||||||
2. Ф: |
|
|
+ |
|
= |
|
, x = 0, y = 0, Ox. |
|
|
x |
y |
2 |
|||||
3. Ф: |
x2 / 9 + y 2 / 4 = 1, Oy. |
|||||||
4. Ф: |
y3 = x2 , y =1, Ox. |
|||||||
5. |
Ф: |
x = 6(t - sin t), y = 6(1 - cos t), Ox. |
||||||
6. |
Ф: |
x = 3cos2 t, y = 4 sin 2 t (0 £ t £ p / 2), Oy. |
||||||
7.Ф: y2 = x, x2 = y, Ox.
8.Ф: y2 = (x -1)3 , x = 2, Ox.
9. Ф: x = 1 - y2 , y = 3 x, y = 0, Ox. 
2
ДВНЗ “Українська академія банківської справи НБУ”
64
10.Ф: y = sin x, y = 0 (0 £ x £ p ), Ox.
11.Ф: y2 = 4x, x2 = 4 y, Ox.
12. Ф: x = 2 cos t, y = 5sin t, Oy.
13.Ф: y = x2 , 8x = y2 , Oy.
14.Ф: y = ex , x = 0, x =1, Ox.
15. Ф: y2 = 4x / 3, x = 3, Ox.
16.Ф: y = 2x - x2 , y = 0, Ox.
17.Ф: y = 
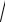1 - x2 , y = x, x = 0, Ox.
18. Ф: x = 7 cos3 t, y = 7 sin3 t, Oy.
19.Ф: x2 /16 + y2 /1 = 1, Ox.
20.Ф: x3 = ( y -1)2 , x = 0, y = 0, Ox.
21.Ф: xy = 4, 2x + y - 6 = 0, Ox.
22. Ф: x = 
3 cos t, y = 2 sin t, Oy.
23.Ф: y = 2 - x2 , y = x2 , Ox.
24.Ф: y = 8 - x2 , y = x2 , Ox.
25.Ф: y2 = (x + 4)3 , x = 0, Ox.
26.Ф: y = x3 , x = 0, y = 8, Oy.
27.Ф: x = cos3 t, y = sin3 t, Ox.
28.Ф: 2 y = x2 , 2x + 2 y - 3 = 0, Ox.
29.Ф: y = x - x2 , y = 0, Ox.
30.Ф: y = 2 - x2 / 2, x + y = 2, Oy.
ДВНЗ “Українська академія банківської справи НБУ”
65