258

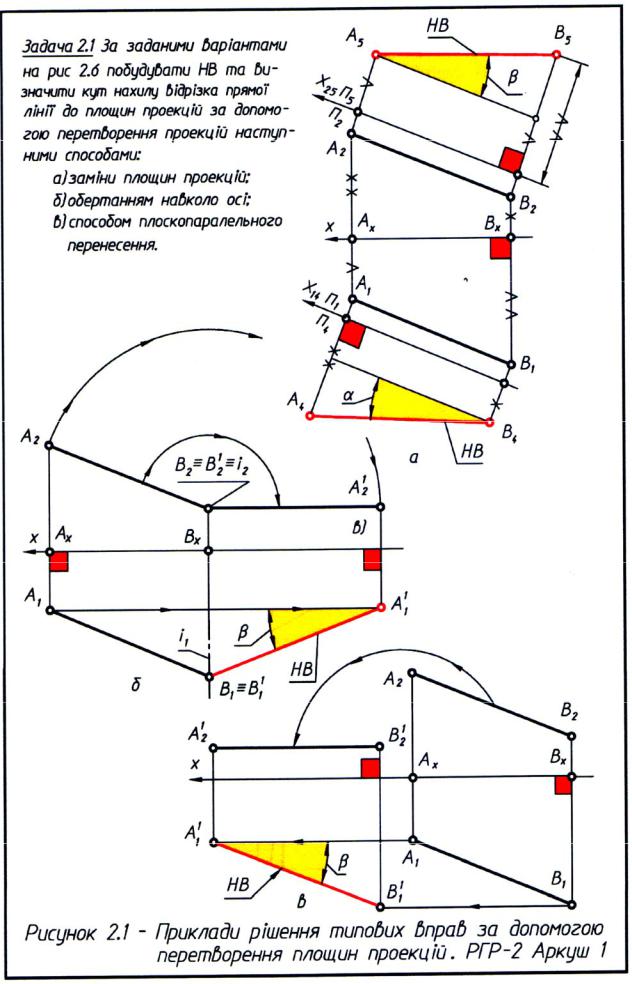
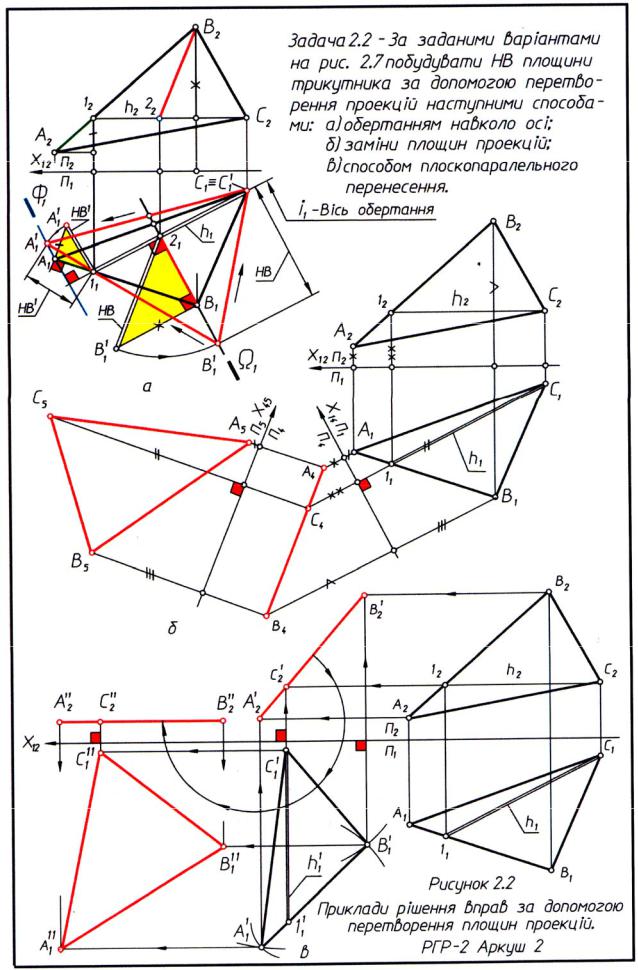
Починають поворот із точки В, яка буде обертатися в площині Ω (Ω1), перпендикулярної осі обертання h1 ≡ i1. Центр обертання 21 точки В утвориться в перетині осі обертання h і площині обертання Ω .

Щоб одержати суміщене положення точки В1 – точку В11 – необхідно в площині Ω відкласти натуральну величину радіуса обертання точки В. Радіус обертання – 2В.

Натуральна величина радіуса обертання знаходиться засобом прямокутного трикутника. З горизонтальної проекції точки В1 відновляють перпендикуляр, на якому відкладають різницю координат точок В і 2 - Ζ, що замірюють на площині проекцій П2. Одержують точку В11.

Після з'єднання точки В11 з 21 одержують натуральну величину радіуса обертання точки В.

Натуральну величину 21В11 відкладають у площині Ω від горизонтальної проекції точки 21 і одержують суміщене положення точки В – точку В1'. Точка А знаходиться на продовженні прямої 1В. Вона буде обертатися в площині Ф, перпендикулярній h. З'єднують проекції точок В1' і 11 прямої і продовжують її до перетину з площиною Ф (площини обертання точки А), одержують суміщене положення точки А – точку А1'. З'єднують суміщене положення проекцій точок А1' і В1' із нерухомою проекцією точки С – точкою С1 і одержують натуральну величину трикутника АВС.

2.3.2 Рис. 2.2 б – Визначення натуральної величини трикутника методом заміни площин проекцій

Щоб площину загального положення перетворити в натуральну величину, необхідно спочатку цю площину перетворити в проеціюючу, а потім і в натуральну величину. Для цього в площині трикутника АВС через точку С проводять горизонталь h. Потім, на будь-якій відстані, перпендикулярно горизонталі проводять нову вісь Х14. У такому разі площину проекції П2 замінюють на нову площину проекцій П4, перпендикулярну П1.

71

З проекцій точок А1, В1, С1 проводять лінії зв'язку перпендикулярно до осі Х14. На цих лініях зв'язку від нової осі Х14 відкладають відрізки, рівні координатам ZA, ZB, ZC, що замірюють на площині проекцій П2. Після з'єднання отриманих проекцій точок А4, В4, С4 одержують пряму – слідпроекцію, в яку спроеціюється трикутник АВС.

Нова вісь проекцій Х2 повинна пройти паралельно сліду-проекції трикутника А4В4С4 на будь-якій відстані від нього. Тепер площину проекції П1 замінюють на П5 перпендикулярно П4.

З проекцій точок А4, В4, С4 проводять лінії зв'язку перпендикулярно Х45 і на них відкладають відрізки, рівні відстаням проекцій точок А1, В1, С1 до осі Х14, від нової осі Х45.

Після з'єднання проекції точок А5, В5, С5 між собою, одержують натуральну величину трикутника АВС.

2.3.3 Рис. 2.2 в – Визначення натуральної величини трикутника способом плоскопаралельного переміщення

Щоб визначити натуральну величину площини загального положення (трикутника АВС), необхідно цю площину перетворити в проеціюючу, а потім вже в натуральну величину – площину рівня. Для цього в площині трикутника АВС через точку С проводять горизонталь h.

Потім, на будь-якій відстані від трикутника АВС розташовують цю горизонталь (h1) перпендикулярно осі Х і зарубками щодо проекцій точок С1' і 11', що лежать на горизонталі, будують проекції точок А1', В1'. З фронтальних проекцій точок А2, В2, С2 проводять вертикальні лінії зв'язку.

Перетин горизонтальних і вертикальних ліній зв'язку дадуть фронтальні проекції точок А2'', В2'', С2''. Після з'єднання їх одержують слід-проекцію трикутника АВС.

Тепер слід-проекцію трикутника А2''B2''C2'' необхідно розташувати на будь-якій відстані паралельно осі Х. Потім проводять горизонтальні лінії зв'язку з проекцій точок A1', B1', C1' і вертикальні лінії зв'язку з проекцій точок

72

A2'', B2'', C2'', у перетині одержують проекції точок A1'', B1'', C1''. Після з'єднання їх між собою, одержують натуральну величину трикутника АВС.

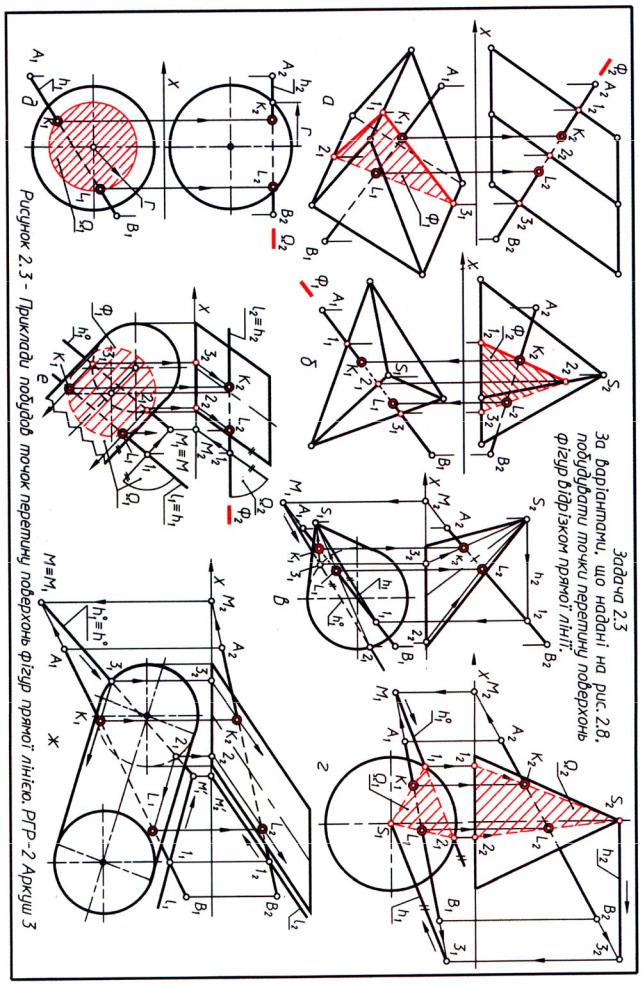
2.4 Пояснення до рішення задач, що надані на рис. 2.3

2.4.1 Рис. 2.3 а – Перетин прямої загального положення АВ із тригранною похилою призмою

Щоб знайти точки перетину прямої АВ із заданою призмою, необхідно пряму АВ укласти у фронтально-проеціюючу площину Ф (Ф2). Побудувати перетин площини Ф із призмою – трикутником 123.

Перетин прямої АВ із сторонами трикутника 123 даэ шукані точки К і L.

2.4.2 Рис. 2.3 б – Перетин прямої загального положення АВ із поверхнею тригранної піраміди

Щоб знайти точки перетину прямої АВ із заданою пірамідою, необхідно пряму АВ укласти в горизонтально-проеціюючу площину. Побудувати перетин піраміди площиною Ф (Ф1) – трикутник 123.

Перетин прямої АВ із сторонами трикутника 123 дає шукані точки К і L.

2.4.3 Рис. 2.3 в – Перетин прямої загального положення з похилим еліптичним конусом із круговою основою

Пряму АВ треба укласти в площину загального положення, задавши її прямими АВ і h, що проходить через вершину конуса S. Через те, що конус розташований на горизонтальній площині проекцій П1, необхідно знайти горизонтальний слід прямої АВ – точку М, через нього провести горизонтальний слід площини h0 (h10) паралельно горизонталі h (h1).

Слід площини h10 розсіче основу конуса в точках 2 (21) і 3 (31).

Після з'єднання їх із вершиною конуса S (S1) одержують фігуру перерізу – трикутник S23, що перетне пряму АВ у шуканих точках К і L.

73

2.4.4 Рис. 2.3 г – Перетин прямої загального положення АВ із прямим круговим конусом

Пряму загального положення треба укласти у площину загального положення, що розсіче конус по найпростішій фігурі – трикутнику 123. Для цього січна площина повинна пройти через вершину конуса S. Січну площину задають прямою АВ і горизонталлю h, що проходить через вершину S. Оскільки основа конуса розташована на площині проекцій П1, необхідно знайти слід площини h0 (h10). Слід площини h0 (h10) пройде через горизонтальний слід М (М1) прямої АВ паралельно h1, тому що всі горизонталі площини паралельні між собою. Слід площини h10 перетне основу конуса в точках 1 (11) і 2 (21), після з’єднання яких із вершиною конуса S (S1) одержують фігуру перетину – трикутник 123. Перетин трикутника 123 із прямою АВ дасть шукані точки К і

L.

2.4.5 Рис. 2.3 д – Перетин горизонталі h із поверхнею сфери

Щоб одержати точки перетину горизонталі h із поверхнею сфери необхідно горизонталь h (h2) укласти в горизонтальну площину рівня Ω (Ω2). Площина Ω перетне сферу по окружності. Перетин горизонталі h (h1) з окружністю дасть шукані точки К і L.

2.4.6 Рис. 2.3 е – Перетин горизонталі h із похилим еліптичним циліндром з круговою основою

Горизонталь h необхідно укласти в площину загального положення, для чого слід задати її двома пересічними прямими h і l, причому пряма l повинна бути паралельна до утворюючої циліндра, тоді циліндр розсічеться по фігурі – чотирикутнику. Оскільки основа циліндра знаходиться на площині проекцій П1, необхідно знайти горизонтальний слід площини Ω – пряму h10. Для цього слід побудувати горизонтальний слід прямої l – М (М1,М2) і через нього провести h10 паралельно h1, тому що всі горизонталі площини паралельні між собою.

74

Слід площини h10 перетне основу циліндра в точках 2 (21) і 3 (31), із яких підуть утворюючі фігури перерізу. Перетин утворюючих із горизонтальною проекцією горизонталі h1 дасть шукані проекції точок К1 і L1. По вертикальних лініях зв'язку будують К2 і L2 на h2.

На цьому ж рисунку додатково задача вирішена шляхом проведення горизонтальної площини рівня Ф (Ф2) через горизонталь h (h2). При цьому в перетині одержують окружність, що проеціюється на П1 у натуральну величину. Перетин окружності з горизонтальною проекцією горизонталі h1 дасть проекції точок перетину К1 і L1.

2.4.7 Рис. 2.3 ж – Перетин прямої лінії загального положення з еліптичним похилим циліндром із круговою основою

Як і у випадку рис. 2.3 е циліндр необхідно розсікти по чотирикутнику. Для цього пряму АВ слід укласти в площину загального положення, задавши її пересічними прямими АВ і l, причому l повинна бути паралельна до утворюючої циліндра. Оскільки основа циліндра розташована на площині проекцій П1, необхідно знайти горизонтальний слід площини h10, який пройде через сліди прямих АВ – точку М і l – точку М'. Слід площини h10 перетне основу циліндра в точках 2 (21) і 3 (31), із яких підуть утворюючі фігури перетину. Перетин цих утворюючих із прямої АВ дасть шукані точки К і L.

2.5 Пояснення до рішення задач, що надані на рис. 2.4

2.5.1Рис. 2.4 а – Переріз піраміди горизонтально-проеціюючою площиною

Горизонтально-проеціююча площина Г (Г1) перетне піраміду по

неправильному чотирикутнику 1234, вершини якого лежать або на основі піраміди (1,4), або на її ребрах (2,3). Натуральну величину перерізу знаходять методом заміни площин проекцій. Для цього нову вісь Х14 проводять через слід-проекцію площини Г1. Потім цю вісь можна розташувати у вільному місці креслення і від неї відкласти координати Z точок 1,2,3,4, що замірюють на

75

площині проекцій П2. Після з'єднання цих точок одержують натуральну величину фігури перерізу.

2 .5.2 Рис. 2.4 б – Переріз прямого кругового конуса горизонтальнопроеціюючою площиною Г

Горизонтально-проеціююча площина Г(Г1) перетинає конус по частині еліпса – більшої його половині. Щоб побудувати еліпс, необхідно знайти його велику і малу осі. Для цього ліву утворюючу конуса необхідно продовжити до перетину зі слідом-проекцією площини Г1. Проекції точок перетину 11 і 21 визначають велику вісь еліпса. Мала вісь еліпса 3141 знаходиться посередині відрізка 11-21, яку визначають його поділом графічно – зарубками. На площині проекцій П2 проекціям більшої і малої осі еліпса відповідають відрізки 1222 і

3242.

Мала вісь еліпса на П2 будується за допомогою вертикальних ліній зв'язку і окружності, на якій лежать точки 3 і 4. Можна взяти додаткові точки 5,6,7,8 та інші, що належать еліпсу, фронтальні проекції яких будуються також за допомогою вертикальних ліній зв'язку і окружностей, на яких лежать ці точки. Це дозволяє отримати більш точну еліптичну криву.

Натуральну величину перетину визначають способом обертання навколо осі і, що проходить через точки 9 і 10 перпендикулярно площині П1. Для цього слід-проекцію площині Г1 повертають до положення паралельного площині проекцій П2. Всі проекції точок 11, 21, 31, 41, 51, 61, 71, 81, що лежать на слідіпроекції площини Г1, сумістяться з віссю Х, тому що основа конуса розташована на площині проекцій П2.

Точки 9 і 10, що лежать на осі обертання, залишаться нерухомими. Після проведення горизонтальних і вертикальних лінії зв'язку, одержують суміщені проекції точок на П2 – 92, 32', 52', 72', 12', 82 ', 62', 42', 102. Після з'єднання вказаних точок плавної лекальної кривої одержують натуральну величину фігури перетину.

2.5.3 Рис. 2.4 в – Переріз прямого кругового конуса горизонтально-проеці- юючею площиною Г

76

Горизонтально-проеціююча площина Г (Г1) розсіче конус по гіперболі, тому що вона паралельна осі конуса. Для побудови гіперболи необхідно знати розчин її гілок і вершину. Розчин (розведення) гілок гіперболи визначають точки 1 і 10, а вершина буде знаходиться на середині цього відрізка – точка 5. Для більш точної побудови гіперболи додатково узяті точки 2, 3, 4, 6, 7, 8, 9, що на фронтальній площині проекцій будуються за допомогою вертикальних ліній зв'язку і окружностей, на яких вони лежать.

Точка 6 є точкою межі видимості на П2. Крива 62, 72, 82, 92, 102 буде видимою, крива – 12, 22, 32, 42, 52, 62 – невидимою. Після з'єднання усіх точок плавної лекальної кривої одержують фігуру перерізу.

Натуральна величина фігури перерізу визначається за допомогою заміни площин проекцій. Нову вісь Х14 проводять на будь-якій відстані паралельно сліду-проекції площини Г1. Слід-проекцію площини Г1 суміщають з віссю Х14 разом із усіма проекціями точок, що розташовані на ній. З проекцій точок 11, 21, 31, 41, 51, 61, 71, 81, 91, 101 проводять лінії зв'язку, перпендикулярні осі Х14 і на них відкладають координати Z, які замірюють на П2 від осі Х до відповідних проекцій точок. Одержують проекції точок 14, 24, 34, 44, 54, 64, 74, 84, 94, 104.

Після з'єднання їх плавною лекальною кривою одержують натуральну величину фігури перерізу.

2.6 Пояснення до рішення задачі, що надана на рис. 2.5

На рис. 2.5 надана тригранна піраміда, що розсічена фронтально-проецію- ючою площиною Р (Р2). У перерізі утвориться трикутник 123, вершини якого знаходяться на ребрах піраміди. Натуральна величина перерізу визначається заміною площин проекцій, для чого у вільному місці креслення проводять вісь Х24, паралельно сліду-проекції площині Р (Р2). Переносять на її слід-проекцію площини Р2 із усіма проекціями точок 12, 22, 32. З цих проекцій проводять лінії зв'язку перпендикулярно осі Х24 і на них відкладають координати Y, що обмірюють від осі Х до проекцій точок 11, 21, 31. Після з'єднання проекцій точок ламаною лінією одержують натуральну величину фігури перерізу.

77