
258
.pdf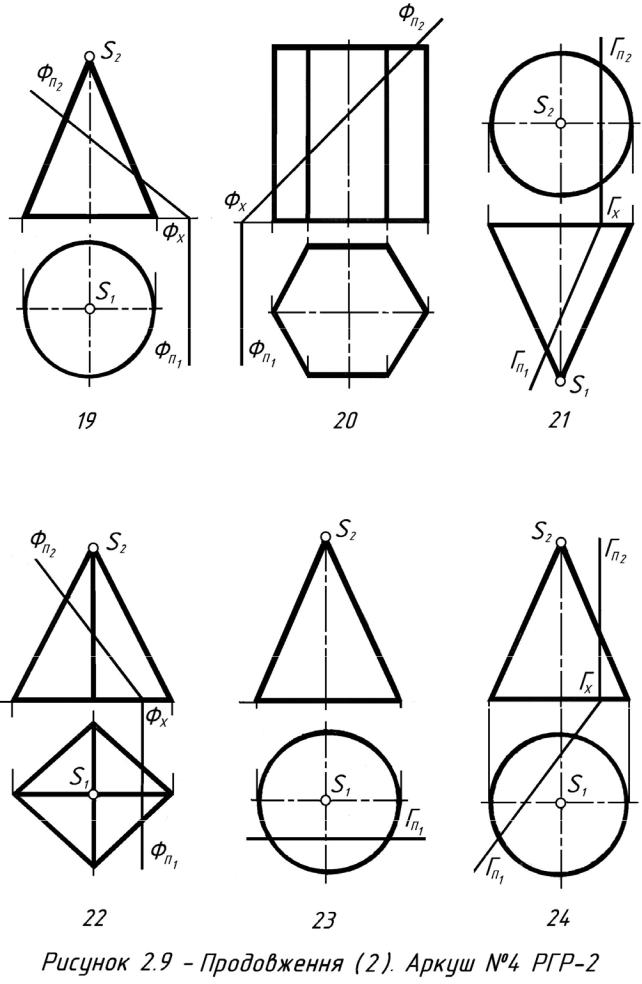
91
92
3 Завдання № 3 ( РГР-3)
Тема: “Побудова лінії перетину поверхонь” Ціль РГР № 3: “Закріпити теоретичні знання, отримані на лекціях за
методикою побудови ліній взаємного перетину різноманітних геометричних багатогранних і криволінійних фігур у різноманітних сполученнях їх у парах, як-от:
-граних з граними,
-граних з криволінійними,
-криволінійних з криволінійними”.
Виробити практичні навички рішення задач на комплексному кресленні – епюрі Монжа по двох заданих проекціях (П1 і П2) з використанням третьої проекції (П3).
3.1Склад і обсяг завдання:
1.Побудова лінії перетину граних поверхонь з граними – формат А3.
2.Побудова лінії перетину граних поверхонь з криволінійними - фор-
мат А3.
3.Побудова лінії перетину криволінійних поверхонь з криволінійними
–формат А3.
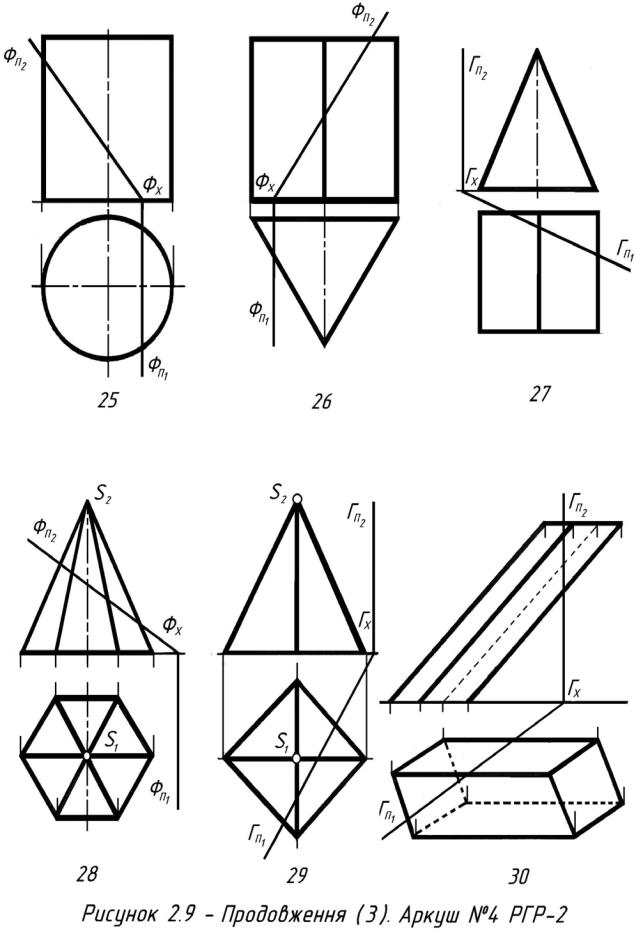
Кожний студент вибирає номер свого варіанта у відповідності зі своїм номером у класному журналі з рис. 3.5, у якому подані тридцять варіантів завдань. Кожний варіант завдання складається з трьох графічних задач.
Задача включає дві проекції фігур фронтальну і горизонтальну . Необхідно побудувати лінію перетину цих фігур спочатку на П2 і П1, а потім її проекцію на П3.
Після вибору свого варіанта, перед початком побудови лінії перетину першої задачі, необхідно ознайомитися з основними положення методики побудо-
93
ви ліній перетину на прикладах рішення типових задач поданих на рис. 3.1, 3.2, 3.3 і 3.4 і з описом методики їхнього рішення.
3.2 Основні положення методики побудови ліній взаємному перетину поверхонь
До основних положень методики побудови ліній перетинання поверхонь фігур, поданих у задачах РГР-3 варто віднести такі аксіоми нарисної геомет-
рії:
-три зображення просторової фігури і всіх її точок на площинах проекцій П1, П2, и П3 комплексного креслення-епюри Монжа пов'язані між собою проек
ційною відповідністю за допомогою ліній зв'язку;
-пряма лінія і площина загального положення перетинаються тільки в од ній точці;
-дві площини перетинаються по відрізку прямої лінії;
-проеціююча грань зображується на площині проекції прямою лінією;
-багатогранні фігури між собою перетинаються по кусочно-ламаним замкненим або разомкненим лініям, що складаються з окремих відрізків ;
-багатогранні і криволінійні поверхні між собою перетинаються по кри-
вим лекальним лініям;
-криволінійні поверхні перетинаються між собою по кривим лініям;
-якщо дві багатогранні фігури перетинаються і кожна з цих фігур на різних площинах проекий займає проецирующее положення, то лінія їхнього взаємного перетину збігається із самою проекцією, що зображується прямою лінією;
-якщо дві криволінійні фігури перетинаються і кожна з цих фігур на різних площинах проекцій займають проеціююче положення, то лінія їхнього взаємного перетину збігається із самою проекцією, що зображується кривою
лінією.
94
У загальному випадку побудову лінії перетину варто почати з аналізу
взаємного положення двох граних фігур по їхніх проекційних зображеннях.
Можливі наступні випадки взаємного положення проекцій фігур:
а) проеціююче положення обох з двох взаємодіючих фігур одночасно на різних площинах проекцій (рис. 3.1, 3.3);
б) проеціююче положення однієї з двох взаємодіючих фігур на однієї площині проекції (рис. 3.2, 3.4).
Після побудови ліній перетину на всіх площинах проекцій потрібно пофарбувати фігури у різний колір для того, щоб контрастно поверхні призм розграничить по лініях перетину.
Цей прийом дозволяє скоріше та наочніше уявити коректність побудов, а також виявити помилки, яки часто мають місце при рішенні графічних задач. Це пов'язано з відсутністю просторового уявлення про взаємодіючі фігури в конкретній задачі.
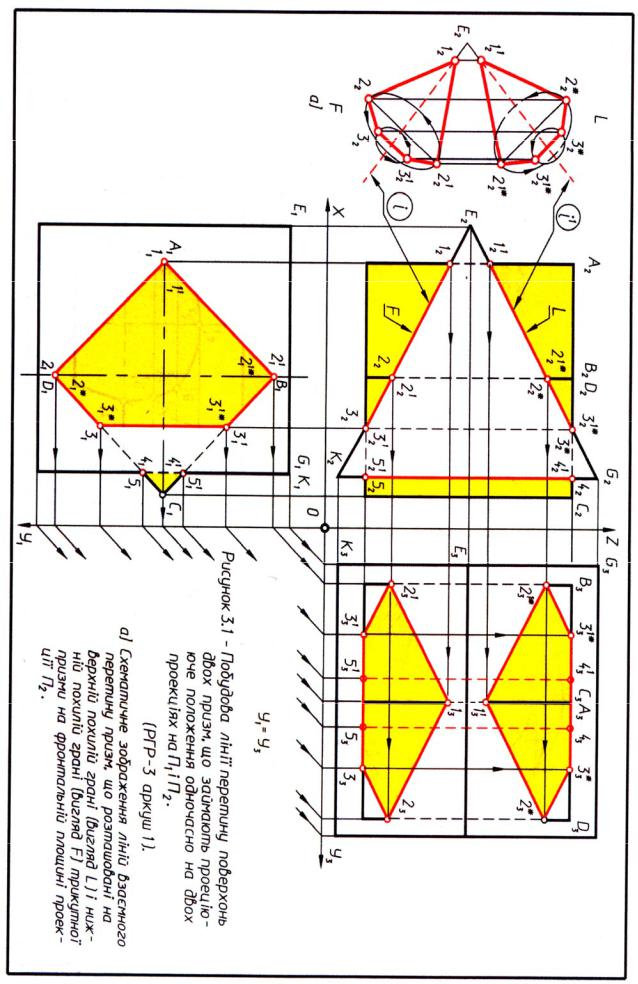
3.2.1Пояснення до рішення задачі наданої на рис. 3.1
1.При побудові лінії перетину граних поверхонь з граними ( рис. 3.1) варто очікувати взаємний перетин площин граней у вигляді кусочно-ламаних ліній, що складені з прямих відрізків. Це випливає з того, що відомо - дві площини перетинаються по прямої лінії.
Побудова лінії перетину слід почати з аналізу взаємного положення
двох граних фігур по їхніх проекційних зображеннях.
З проведеного аналізу взаємодії площин граней трикутній та чотирьох кутній призм коли дві взаємодіючі фігури займають проеціююче положення одночасно на двох площинах проекцій видно, що на площинах проекцій П1 і П2 лінії перетину граней фігур збігаються з їхніми зображеннями у вигляді ліній:
112 – 312* зверху і 12 – 32 знизу.
Ці лінії на П1 і П2 пофарбовані в червоний колір.
95
Насправді, після розгляду вказаних ліній по напрямках погляду по L і F на рис. 3.1 а) на П2 це - дві кусочно-замкнені лінії:
- зверху - 112 – 212* – 312* – 3*2 – 2*2 – 112 і - знизу - 12 – 22 – 32 – 312 – 212 -12.
Ці лінії обмежують дві п'ятикутні плоскі фігури, що подані у червоному колірі на просторовому схематичному зображенні зліва від площині проекції П2 на виглядах L і F відповідно. Ці зображення надані як результат обернення фігур відносно їх осей симетрії із проеціюючего положення відносно П2 на кут
90º.
На горизонтальної площині проекції П1 (рис. 3.1 на вигляді зверху) лінія перетину двох призм зображується однієї кусочно-замкненою лінією, що обмежує п'ятикутню плоску “верхню” фігуру
|
111 – 21* – 31* - 311* - 211* - 111 |
||
|
видимі відрізки лінії фігури |
||
і “нижню” фігуру |
11 – 21 – 31 – 311 - 211 - 111 , |
||
|
|
|
|
|
невидимі відрізки ліній фігури |
||
яка знаходиться під верхньою і збігається з останньої.
Побудова ліній перетину призм на профільної площині проекцій П3 виконується з використанням властивості проекційній відповідності характерних та проміжних точок, що належать лініям перетину одночасно всім площинам проекцій. До таких точок відносяться всі точки з’єднання кінців відрізків – точки вершин кутів двох п'ятикутників.
3.2.2 Пояснення до рішення задачі наданої на рис. 3.2
Для вправи, що надана на рис. 3.2, коли одна з фігур займає проеціююче положення стосовно площині проекції, лінія перетину, що належить цей фігурі, буде збігатися з її зображенням у виді прямої лінії у межах границь взаємної приналежності проекцій обох фігур, як проеціюючей так і непроеціючей.
96
Проеціююче положення лінії перетину знаходиться на П2 - окружність діаметром дорівнюючим відрізку 52 - 512 , яка і зображується цім же відрізком. А також двома відрізками під нахилом. Це відрізки:
42 … 12 і 12 … 412.
Вони пофарбовані у червоний колір на П2.
Насправді, на підставі збірної властивості проеціюючих граней призми, лінії перетину граней з поверхнею конуса - криві замкнуті лінії - ліва і права. Ці лінії одночасно належать як граням, так і поверхні конуса.
Для побудови ліній перетину поверхонь на П1 необхідно застосувати допо міжні горизонтальні площини рівня, наприклад - ωί2. Ці площини рівнобіжні (паралельні) основі конуса і перпендикулярні П2, на якої вони зображуються відрізками прямих ліній.
При перетину поверхні конуса горизонтальними площинами рівня на П1 будуть утворюватися окружності, а при перетину призми - відрізки по двох похилих гранях, так називані “утворюючі” (образующие). Від точок перетину граней площинами рівня на горизонтальну площину проекцій підуть лінії зв'язку, що зустрінуться з відповідними дугами окружностей і утворять точки на П1, що і належать лінії перетину призми з конусом. Після з’єднання цих точок за допомогою лекала будуються плавні криві лінії перетину фігур на П1:
-ліва крива - 111 – 211 – 311 – 41 – 31 – 21 - 11 - суцільна товста крива;
-права крива - 11 – А1 – В1 – 411 – В11 – А11 – 111 – суцільна товста крива;
-крива посередині – окружність з діаметром дорівнюючим відрізку
-51 - 511 – штрихова лінія тому, що проекція лінії перетину невидима.
Всі побудовані криві пофарбовані у червоний колір.
На профільної проекції П3 лінію перетину треба будувати з використанням проекційної відповідності характерних та проміжних точок на всіх площинах проекцій. Ця лінія має вигляд плавної кривої лінії, яка складається з двох частин. Одна та, що спостерігач бачить і друга, та що прячеться за ній. Тому на П3 мають місце подвійні точки.
97

Ці дві лінії мають перегин по прямої 1 - 11 у просторі і 13 - 113 – на П3. У зазначених кінцях цього відрізка вони стикуються і утворюють замкнену криву лінію, що “обрамляє” вихідний отвір, по якому конус пронизує призму.
На П3 цей отвір утворюється з'єднанням лекальної кривої характерних і проміжних точок наступним ланцюжком:
13 – 23 – 33 – 43 –313 – 213 – 113 – 113 - А13 – В13 – 413 – В3 – А3 - 13
видима крива невидима крива
Вхідний нижній отвір конуса у площину основи призми на П3 утворено лінією окружності, що зображується відрізком прямої С3 – D3. Всі лінії перетину поверхонь конуса і призми на П3 пофарбовані у червоний колір, а поверхонь конуса - в жовтий.
3.2.3 Пояснення до рішення задачі наданої на рис. 3.3
Для вправи, що надана на рис. 3.3, коли перетинаються дві криволінійні фігури циліндр і напівциліндр, на горизонтальної и фронтальної площинах проекцій лінії перетину поверхонь знаходяться на підставі збірних властивостей проеціюючих поверхонь. На підставі аналізу взаємодії поверхонь криволінійних фігур неважко встановити, що лінія перетину поверхонь збігається з самою проекцією, яка також зображується лініями – на П1-
окружністю,
на П2 – частиною дуги окружності 12 …92. На профільної площині проекції П3 лінія перетину будується на підставі проекційної відповідності точок поверхонь обох фігур. Лінія перетину двох фігур на площині П3 є лекальна плавна крива лінія (аналог ювелірної прикраси - “буси”):
13 – 23 – 33 – 43 – 53 – 63 – 73 – 83 – 93 – 813 – 713 – 613 – 513 – 413 – 313 – 213 - 13
видима крива |
невидима крива |
видима крива |
Вказані лінії пофарбовані в червоний колір.
3.2.4 Пояснення до рішення задачі наданої на рис. 3.4
Для вправи, що надана на рис. 3.4, коли взаємодіють дві криволінійні фігури циліндр і сфера, побудову лінії перетину фігур треба почати з аналізу їхнього взаємного положення на площинах проекцій.
98
З аналізу випливає, що на П1 поверхня циліндра займає проеціююче положення і лінія перетину поверхонь сфери і циліндра по збірній властивості проеціюючей поверхні, збігається з частиною дуги окружності циліндра, розташованої зліва від його вертикальної осі симетрії.
На площині проекції П2 лінію перетину треба шукати з використанням характерних і проміжних точок, що розташовані на лінії-проекції з використанням проекційної відповідності їх на всіх площинах проекцій. Крім того, треба використати допоміжні проеціюючи площини - посередники (фронтальну площину рівня), що перетинають проеціюючи зображення лінії перетину на циліндрі, від якої відходять лінії зв’язку на проекцію П2, де зустрічаються з дугами окружностей, радіуси яких вимірюються на П1 від вертикальної осі симетрії до крайньої утворюючої основи сфери (окружність).
Характерні точки в даному випадку:
11 – точка видимості, що розташована на діаметрі основи циліндра; 12 – проекція точки видимості на П2, розташована по приналежності на
крайньої утворюючої сфери – дуги окружності дорівнюючої діаметру сфери; 71, 711 – точки перетину окружностей основаній сфери і циліндра; 72, 712 - іх проекції на П2, що визначені по проекційної відповідності; 21…61 і 211…611 – проекції проміжних точок на П1; 22…62 і 212…612 – проекції проміжних точок на П2.
Побудова лінії перетину поверхонь сфери і циліндра на П2 здійснюють шляхом з'єднання побудованих точок за допомогою лекала. Після визначення лінії перетину фігур на П1 і побудови лінії перетину на П2 необхідно побудувати лінію перетину на П3 з використанням проекційної відповідності точок лінії перетину на всіх площинах проекцій. Для чого потрібно провести лінії зв’язку от однойменних проекцій однієї і той же точки з різних площин проекцій в напрямку до П3 поки вони не перетнуться у точки. Ця точка і буде побудованою за принципом проекційної відповідності. Інші точки будують аналогічно.
99
100
