

ТЕОРИЯ ИГР
Графический метод решения игр типа 2 n × и 2 m ×
Выигрыш игрока А, если он придерживается оптимальной стратегии, не зависит от того, в каких пропорциях игрок В применяет стратегии, поэтому неизвестные определяются из системы уравнений
Частоты в
игрока В определяются из соотношения
11
ТЕОРИЯ ИГР
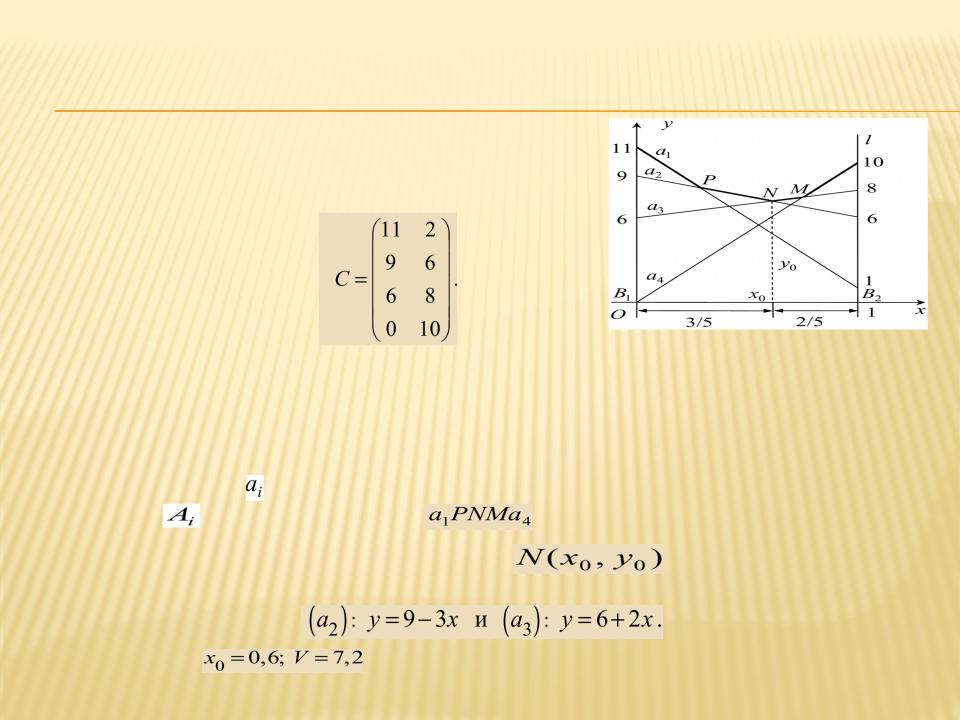
Графический метод решения игр типа 2 n × Пример . Пусть игра задана матрицей
Найти оптимальные и определить цену игры.
Решение.
Воспользовавшись тем, что игрок B располагает двумя чистыми
стратегия-ми, построим прямые |
, соответствующие выигрышам |
||
игрока А при чистых стратегиях |
и ломаную линию |
, |
|
огибающую график сверху. |
|
|
|
Эта ломаная достигает минимума в точке |
, которая |
||
является |
|
|
|
пересечением прямых |
|
|
|
Следовательно, |
, и оптимальной стратегией игрока В |
||
является стратегия |
|
|
12 |

ТЕОРИЯ ИГР
Графический метод решения игр типа 2 n × и 2 m ×
Цена игры V = 7,2.
Полезными стратегиями игрока А являются стратегии
.
Найдем их частоты
13

ТЕОРИЯ ИГР
Прямоугольные игры ( без седловых точек): смешанные стратегии
Пример. Рассмотрим игру с платежной матрицей, показанной в таблице 1. Платежная матрица не имеет седловой точки, т. к. в этой игре ни один из участников игры не может выбрать один план в качестве своей оптимальной стратегии.
Следовательно, каждый игрок должен найти некоторую «смешанную стратегию»для максимизации своего выигрыша или минимизации
Допустим, например, что А решает играть половину времени по плану Р, а половину по плану Q. Если В при этом будет все время играть
плану S, то ожидаемый выигрыш для А будет
а если В будет все время играть по плану Т,
то ожидаемый выигрыш игрока А
будет
14

ТЕОРИЯ ИГР
Прямоугольные игры ( без седловых точек): смешанные стратегии
Допустим далее, что Втакже применяет смешанную стратегию и в половине случаев выбирает план S, а в половине Т, причем каждый выбор определяет случайно. В этом случае ожидаемый выигрыш игрока Абудет
Подобным образом можем подсчитать, каков ожидаемый выигрыш А при
других смешанных стратегиях. Например, если А играет в четверти случаев план Р, a Q — в трех четвертях, в то время как В играет одну треть раз S, а две трети Т,то ожидаемый выигрыш Абудет
Возникает вопрос: какова оптимальная смешанная стратегия для игро ков? Из приведенных примеров видим, что выигрыш А меняется от 1,5
долларов до 4 долларов. Хотим узнать, не может ли игрок Аобес печить себе некоторый минимум выигрыша и каков он?
Подобным образом, может ли Взастраховаться от проигрыша
больше некоторого максимального?
На эти вопросы можно ответить положительно. Математическая теория игр дает доказательство того, что всегда существуют
оптимальные стратегии и способы их нахождения.
15

ТЕОРИЯ ИГР
Прямоугольные игры ( без седловых точек): смешанные стратегии
Рассмотрим теперь, как могут быть найдены оптимальные стратегии этой игры и каковы ожидаемые значения выигрыша и проигрыша для игроков.
Пусть Аиграет Рс частотой х, a Q с частотой 1 — х. Тогда, если
В будет играть все время S, выигрыш А будет
Если Вбудет все время играть Т, выигрыш Абудет
Математически можно показать, что если Авыберет х так, что то для него это будет оптимальной стратегией. Итак,
В результате получаем
16

ТЕОРИЯ ИГР
Прямоугольные игры ( без седловых точек): смешанные стратегии
Таким образом, независимо от частот, с которыми Виграет S или Т, Авсегда выигрывает 3 доллара. (Если, например, В играет S с частотой и Т с частотой то ожидаемый выигрыш для А будет
и так же при любом выборе частот для В.) Следовательно, выбором частот 1/3 и 2/3 А получает обеспеченный выигрыш в 3 доллара.
Тот же самый метод можно применить к игроку В. Обозначим частоту выбора плана S буквой y, тогда частота выбора Тбудет 1 - y . Для оптимальной
стратегии имеем:
Заметим, что |
для игры с нулевой суммой. |
Полным решением данной игры будет: (1) Аследует играть Ри Q соответственно
с
частотами 1/3 и 2/3; (2) Вследует играть S и T с частотами 2/5 и 3/5; (3) цена игры — 3 доллара.
17

ТЕОРИЯ ИГР
Основные теоремы для прямоугольных игр.
Платежи для прямоугольных игр всегда могут быть заданы в виде матрицы
m x n где игрок А имеет mвозможных планов, В имеет пвозможных планов и платежная матрица есть матрица (см. табл. 2).
Таблица 2
Математически можно показать, что (1) каждой прямоугольной игре соответствует
определенное значение цены g; это значение
единственно; (2) существует оптимальная стратегия
игрока А, т. е., существуют частоты такие, что
и если игрок А
играет, применяя план I с частотой х1, план II с частотой
х2 …., план m c частотой Хm , то он может обеспечить
себе средний выигрыш не менее g, где g— цена игры;
(3) также и для игрока Всуществует оптимальная
стратегия
такая, что, если он применяет планы I, II, . . . , пс частотами y1,y2,…yn |
он |
обеспечивает себе проигрыш не больше g |
18 |

ТЕОРИЯ ИГР
Основные теоремы для прямоугольных игр
Для прямоугольной игры, матрица которой имеет седловую точку ( i0 , j0), имеем следующее решение
Общее решение прямоугольных игр. Можно показать, что неизвестные и g могут быть найдены из следующих соотношений:
Соотношение (3) в действительности представляет собой п неравенств, по одному неравенству для каждого j. Соотношение (4) представляет
собой nнеравенств. Таким образом, имеем m+n+1 неизвестных с
m+n+2 соотношениями (с дополнительными ограничениями
так как отрицательные частоты не имеют смысла).
19

ТЕОРИЯ ИГР
Основные теоремы для прямоугольных игр
Теоремы предыдущей части гарантируют существование решения, удовлетворяющего этим соотношениям.
Они гарантируют также единственность g.Однако для |
игра |
может иметь несколько или даже бесконечное множество решений. |
|
Пример. Для игры, представленной в таблице 1, неизвестными будут
и g. Соотношения следующие
(5)
(6)
(7)
(8)
(9)
(10)
Такие задачи могут быть решены при помощи «обычной алгебры», графическим способом, применением матричной алгебры или
итеративным методом.
20
