4.2.7. Примеры вычисления вектора угловой скорости.

1. Углы Эйлера

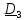
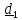
Рис. 4.9 Рис 4.10.

линия узлов

Традиционно углы Эйлера вводятся следующим образом. Переход из отсчетного положения в актуальноеосуществляется тремя поворотами (рис.4.9):

1. Поворот вокруг на уголпрецессии При этом переходит в положение,(в).

Этот поворот описывается тензором

2. Поворот вокруг на уголнутации. При этом , .

Этот поворот описывается тензором

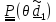
4. Поворот вокруг на уголсобственного (чистого) вращения – тензор .

Таким образом, результирующий тензор поворота равен

(4.26)

Для наглядности на рис.4.10 изображен волчок и углы Эйлера, описывающие его ориентацию.

Покажем, что традиционная последовательность поворотов (4.26) может быть заменена на последовательность поворотов на те же самые углы вокруг неподвижных осей:

1. Поворот вокруг на уголсобственного (чистого) вращения

2. Поворот вокруг на уголнутации . .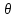

4. Поворот вокруг на уголпрецессии

Поскольку , то по теореме (4.19)

,

.

Подставляя эти выражения в (4.26), получим с учетом ))

. (4.27)

Разумеется, преимущество (4.27) по сравнению с (4.26) в том, что оси поворотов неподвижны.

Вектор угловой скорости по теореме о сложении угловых скоростей (4.23) равен

.

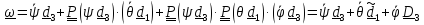Это же (правильное) выражение обычно получают из (4.26), применяя правдоподобные рассуждения о сложении « бесконечно малых» поворотов; применив их к другой последовательности поворотов, например (4.27), получим абсолютно неверный результат

.

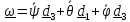Из (4.27) видно, что при малом угле нутации , когдатензор поворота

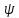- углы ив линейном приближении становятся

неразличимы и входят в уравнения в виде суммы (+. В этом неудобство углов Эйлера.

2. Самолетные (корабельные) углы.

Этого недостатка лишены самолетные (корабельные) углы (рис.4.11).

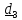
Рис.4.11

Переход из отсчетного положения в актуальноеможно осуществить

тремя поворотами (повернуть самостоятельно!) (рис.4.11):

1. Поворот вокруг на уголрысканья , при этом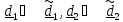

2. Поворот вокруг на угол тангажа, при этом

4.Поворот на угол крена вокруг.

Тензор поворота равен (4.28)

Выражение «можно осуществить» неслучайное; нетрудно понять, что возможны и другие

варианты, например, повороты вокруг фиксированных осей. Применяя теорему о тензоре

поворота с повернутой осью (4.19) из того, что ,

будем иметь

=

=.

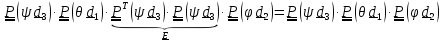Таким образом, получили следующую композицию поворотов:

1. Поворот вокруг на уголкрена (рискуя сломать крылья)

2. Поворот вокруг на уголтангажа (подъем «носа»)

4. Поворот вокруг на уголрысканья

Тензор поворота и вектор угловой скорости имеют вид

(4.29)