Vischa_matematika_Chastina_2_Denisyuk_Repeta

http://vk.com/studentu_tk, http://studentu.tk/

3.5. Знайдіть найбільше та найменше значення функції z(x, y) у замкненій області D :

3.5.4.z = xy(3 − x − y) , D = {(x, y) x ≥ 0, y ≥ −2, x + y ≤ 6} .

3.5.5.z = x3 + 3y 2 , D = {(x, y) x2 + y 2 ≤ 4} .

3.5.8.z = (x − y)2 + y 2 + 2x , D = {(x, y) x ≤ 0, y ≤ 0, x + y + 4 ≥ 0} .

3.5.9.z = 2x3 + 3y 2 , D = {(x, y) 1 ≤ x2 + y 2 ≤ 9} .

62

http://vk.com/studentu_tk, http://studentu.tk/

3.5.21. z = 2x2 + y2 + 2xy − 6x − 4 y, D = {(x, y) x ≥ −1, y ≥ 0, x + y ≤ 3} .

3.5.22.z = 6xy − 9x 2 − 9 y 2 + 4x + 4 y , D = {(x, y) 0 ≤ x ≤ 1, 0 ≤ y ≤ 2} .

3.5.23.z = 4x − 2y + x − y + 1, D = {(x, y) 12 ≤ x ≤ 3, 13 ≤ y ≤ 2} .

3.5.29.z = 5x 2 − 3xy + y 2 , D = {(x, y) 0 ≤ x ≤ 2, 0 ≤ y ≤ 2} .

3.5.30.z = x2 + 2xy − 1, D = {(x, y) y ≤ 0, y ≥ x2 − 4} .

Тема 4. КОМПЛЕКСНІ ЧИСЛА

Поняття комплексного числа. Дії над комплексними числами в алебраїчній формі. Геометричне зображення комплексних чисел. Модуль і аргумент комплексного числа. Тригонометрична і показникова форми комплексного числа. Дії над комплексними числами у тригонометричній формі.

Література: [2, розділ 1, стор. 18—25], [3, розділ 7, §1], [4, §3], [5, розділ 3, §6], [6, розділ 7, розділ 7, §1—§8], [8, 1 част.,

розділ 6].

Т.4 ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ

4.1. Поняття комплексного числа

Вираз

z = a +bi,

де а і b — дійсні числа, i = −1 — уявна одиниця ( i2 = −1), називають комплексним числом. Таку форму запису комплексного числа називають

63

http://vk.com/studentu_tk, http://studentu.tk/

алгебраїчною, число а — дійсною частиною комплексного числа z, а b — уявною частиною z і позначають

a = Re z, b = Im z.

Позначення дійсної й уявної частин комплексного числа z походить від

( z1 = z2 ) тоді і тільки тоді, коли рівні їхні дійсні та уявні частини, тобто

a1 = a2 і b1 = b2 .

Комплексне число z = a +bi дорівнює нулю тоді і тільки тоді, коли

a = b = 0 .

Поняття «більше—менше» для комплексних чисел не існує.

4.2. Дії над комплексними числами в алгебраїчній формі

Дії над комплексними числами z1 = a1 +b1i та z 2 = a2 +b2i викону-

ють за такими правилами: 1) додавання:

z1 + z2 = a1 + a2 +(b1 +b2 )i ;

4.3. Геометричне зображення комплексних чисел. Модуль і аргумент комплексного числа

Між множиною С усіх комплексних чисел і всіма точками площини існує взаємно однозначна відповідність, іншими словами, кожному комплексному числу z = a +bi ставиться у відповідність точка площини (a, b) , і

навпаки, кожній точці з координатими (a, b) ставиться у відповідність комплексне число z = a +bi . На рисунку 1.14 комплексне число z = a +bi зображається точкою M (a, b) . Таку площину умовно називають комплекс-

64

http://vk.com/studentu_tk, http://studentu.tk/

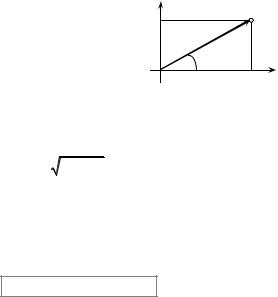
ною площиною змінної z, вісь Ox — дійсною, а вісь Oy — уявною віссю. Комплексне число z = a +bi можна також зображувати вектором, початок якого міститься у точці О (0; 0), а кінець — у точці M (a, b) .

дає комплексному числу z = a +bi , називають аргументом комплексного

числа z (z ≠ 0) і позначають ϕ = arg z.

Кожне ненульове комплексне число має безліч аргументів. Усі вони задаються формулою

Arg z= arg z + 2πn , n ],

http://vk.com/studentu_tk, http://studentu.tk/

Відшукання аргументу комплексного числа рекомендуємо розпочинати

згеометричного зображення цього числа.

4.4.Тригонометрична форма комплексного числа

Зрисунка 1.14 видно, що a = ρcos ϕ , b = ρsin ϕ. Тоді комплексне число z = a +bi можна подати у вигляді

Праву частину формули (1.17) називають тригонометричною формою комплексного числа z.

4.5.Дії над комплексними числами

утригонометричній формі

Нехай z1 = ρ1 (cos ϕ1 +i sin ϕ1 ) , z2 = ρ2 (cos ϕ2 +i sin ϕ2 ) .

Знайдемо добуток

z1 z2 = ρ1ρ2 (cos ϕ1 +i sin ϕ1 ) (cos ϕ2 +i sin ϕ2 ) =

=ρ1ρ2 (cos ϕ1 cos ϕ2 −sin ϕ1 sin ϕ2 +i(sin ϕ1 cos ϕ2 +sin ϕ2 cos ϕ1 ) =

=ρ1ρ2 [cos(ϕ1 +ϕ2 ) +i(sin(ϕ1 +ϕ2 )] .

Висновок. Під час множення комплексних чисел їхні модулі перемножують, а аргументи додають.

Піднесення комплексного числа, заданого у тригонометричній формі, до n-го степеня, де n N, виконують за формулою Муавра:

Ділення комплексних чисел, заданих у тригонометричній формі:

z1 = ρρ1 (cos(ϕ1 −ϕ2 ) +i sin(ϕ1 −ϕ2 )).

z2 2

Корінь степеня n, де n — ціле додатне число, з комплексного числа z = ρ(cos ϕ+i sin ϕ) добувають за формулою:

66

http://vk.com/studentu_tk, http://studentu.tk/

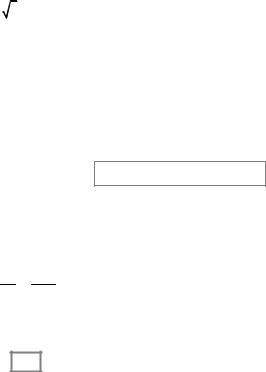
де k = 0, 1, 2, ..., n −1. Отже, існує n різних значень кореня n-го степеня з числа z. Усім цим значенням відповідають точки площини, які лежать на колі радіуса n ρ з центром у початку координат і є вершинами правильного n-кутника.

4.6. Показникова форма комплексного числа

За формулою Ейлера

eiϕ = cos ϕ+i sin ϕ .

Звідси випливає, що комплексне число, записане у тригонометричній формі, можна подати ще й так:

z = ρ(cos ϕ+i sin ϕ) =| z | eiϕ.

Вираз | z | eiϕ називають показниковою формою комплексного числа z. Нехай z1 =| z1 | eiϕ1 , z2 =| z2 | eiϕ2 . Тоді:

1)z1 z2 =| z1 | | z2 | ei(ϕ1+ϕ2 ) ;

2)z1 = | z1 | ei(ϕ1−ϕ2 ) ; z2 | z2 |

3) zn =| z |n einϕ .

Т.4 ПРИКЛАДИ РОЗВ’ЯЗАННЯ ТИПОВИХ ЗАДАЧ

67

http://vk.com/studentu_tk, http://studentu.tk/

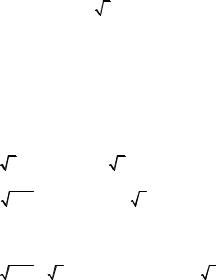
2. Обчисліть i18 +i25 +i36 +i−1 .

Розв’язання. Враховуючи рівності i2 = −1, i3 = −i, i4 =1, маємо

i18 +i25 +i36 +i−1 = i16+2 +i24+1 +i36 −i =

=(i4 )4 i2 + (i4 )6 i + (i4 )9 −i = i2 +i +1−i = 0 .

3.Знайдіть дійсну та уявну частини комплексного числа

4. Знайдіть модуль й головне значення аргументу комплексних чисел, запишіть ці числа у тригонометричній формі:

a) z1 = 3 ; б) z2 = 2i ; в) z3 = −1;

г) z4 =1+i ; д) z5 =1−i 3 ; е) z6 = −2−i .

Розв’язання. Вказаним числам відповідають на площині точки M1 −M6

(рис. 1.15).

За формулами (1.15) — (1.17) дістаємо:

68

http://vk.com/studentu_tk, http://studentu.tk/

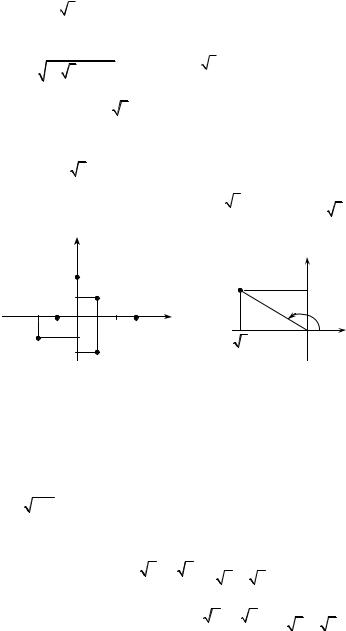
5. Знайдіть (− 3 +i)13 .

Розв’язання. Запишемо дане число у тригонометричній формі (рис. 1.16):

6. Розв’яжіть рівняння z4 +16 = 0 .

Розв’язання. Запишемо рівняння у вигляді z4 = −16 . Тепер подамо число –16 у тригонометричній формі: −16 = 16(cos π + i sin π).

Використовуючи формулу (1.19), дістаємо

Послідовно визначаємо усі чотири корені даного рівняння:

69

http://vk.com/studentu_tk, http://studentu.tk/

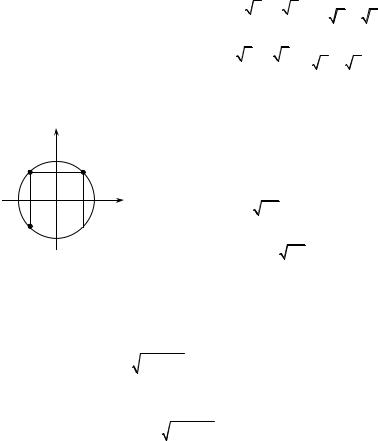
З погляду геометрії одержані корені — вершини квадрата, вписаного у коло радіуса 2 (рис. 1.17).

8. Розв’яжіть рівняння | z | −2z = −1−8i.

Розв’язання. Невідоме число z запишемо в алгебраїчній формі: z = x +iy . Тоді

x2 + y2 −2x −2 yi = −1−8i .

З умови рівності комплексних чисел одержуємо систему двох рівнянь із двома невідомими:

http://vk.com/studentu_tk, http://studentu.tk/