Лабораторная работа

ИЗУЧЕНИЕ ПРОЦЕССОВ, ПРОИСХОДЯЩИХ В ЦЕПИ

ГАРМОНИЧЕСКОГО ПЕРЕМЕННОГО ТОКА

Приборы и принадлежности: катушка индуктивности, батарея конденсаторов, реостат, амперметр, вольтметр, источник переменного напряжения.

Цель работы: определить индуктивность катушки, емкость конденсатора, экспериментально проверить закон Ома для полной цепи переменного тока.

ТЕОРИЯ

Переменным током называется такой электрический ток, который с течением времени изменяется по величине и направлению.

Гармоническим ( синусоидальным) током называется переменный ток, который с течением времени изменяется по закону синуса или косинуса:

i = I_m sin ( t -  )

или i = I_m cos ( t -  )

Здесь i - мгновенное значение переменного тока - величина тока, соответствующая данному моменту времени,

I_m - максимальное ( амплитудное ) значение тока,

(t -  )- фаза синусоидального тока,

 = 2 - круговая ( циклическая ) частота тока,

 - частота тока,

 - начальная фаза.

Гармонический ток создается синусоидальным или косинусоидальным напряжением той же частоты

u = U_m sint

u = U_m cost

Для характеристики силы переменного тока сопоставляют его среднее тепловое действие с тепловым действием постоянного тока соответствующей силы и вводят понятие действующего ( эффективного) значения переменного тока. Эффективное значение переменного тока численно равно значению такого постоянного тока, который выделяет в данной цепи за единицу времени такое же количество тепла как и данный переменный ток. Математически эта величина равна среднеквадратичному за период значению силы переменного тока и связана с его максимальным значением соотношением:

I_эф =

Аналогично определяется и эффективное значение напряжения

U_{эф =}

При расчете цепей переменного тока приходится производить сложение и вычитание синусоидальных токов или напряжений, имеющих одинаковую частоту, но в общем случае различные амплитуды и начальные фазы. Решение подобных задач значительно облегчается, если применить метод векторных диаграмм, основанный на изображении величины тока или напряжения с помощью вращающихся векторов. Для этого амплитудные значения тока I_m и напряжения U_m представляют векторами, вращающимися в плоскости OXY ( обычно вращение берут против часовой стрелки ) вокруг начала координат O с угловой скоростью, соответствующей циклической частоте  . Угол поворота векторов t отсчитывают от оси OX. На рис.1а изображено положение векторов для момента времени t = 0, на рис.2б для времени t>0. Проекции векторов I_m и U_m на ось OY будут определять мгновенные значения тока i=I_msint и напряжения U=U_msint

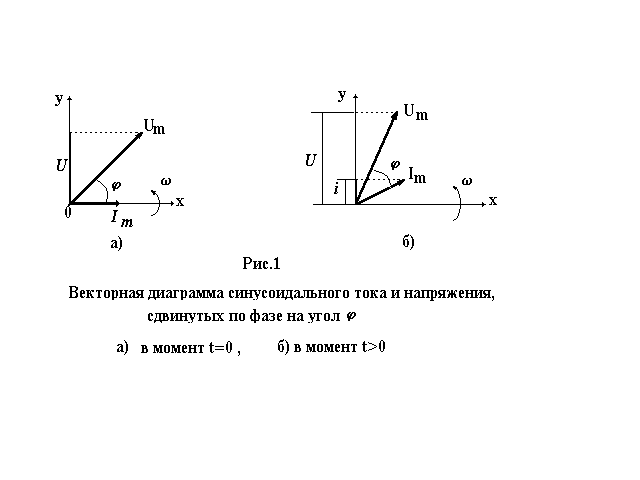
Цепь переменного тока с активным сопротивлением

Активным ( омическим ) сопротивлением в цепях переменного тока называют сопротивление, в котором происходит необратимый процесс превращения электрической энергии в какой-либо иной вид, например, в тепловую. Это сопротивление зависит от материала проводника, его размеров и формы. Для однородного по составу проводника при постоянном сечении S и длине l сопротивление рассчитывается по формуле R=, где  - удельное сопротивление,характеризующее материал проводника, зависит от температуры: =₀(1+t⁰). Поэтому активное сопротивление зависит также от температуры проводника.

В цепи переменного тока, содержащей активное сопротивление ( Рис.2а), как и в случае постоянного тока, выполняется закон Ома, который может быть применен к мгновенным, амплитудным и эффективным значениям тока и напряжения:

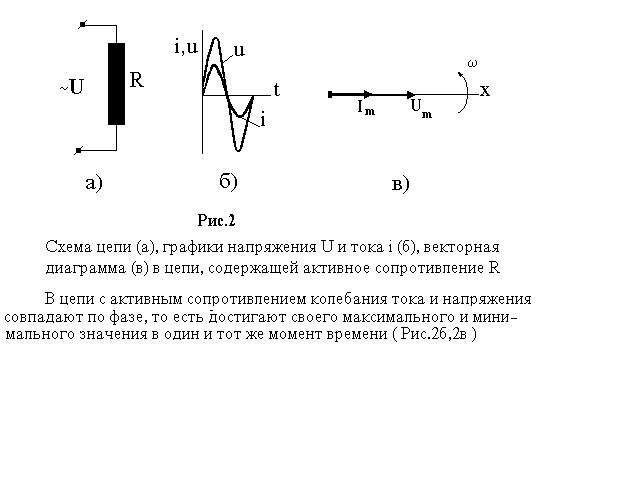
i= ; I_m= ; I_эф=

Индуктивность в цепи переменного тока

Рассмотрим цепь переменного тока, в которую включена катушка индуктивностью L ( Рис.3а). Пусть напряжение в цепи изменяется по закону u=U_msin t . При протекании переменного тока через катушку на концах катушки возникает ЭДС самоиндукции &_i = - L .

Если активное сопротивление катушки принять равным нулю, то внешнее приложенное напряжение U, согласно закону Ома для цепи, содержащей ЭДС, по величине равно и по направлению противоположно ЭДС самоиндукции, то есть

U=-&_i = L

или U_msin t=L , откуда sin t и di = sin t dt интегрируя последнее выражение получим:

i = - t = t - 2 ),

где - амплитуда тока.

Тогда по аналогии с законом Ома для участка цепи можно записать, что I_m=, где величину можно рассматривать как индуктивное сопротивление.

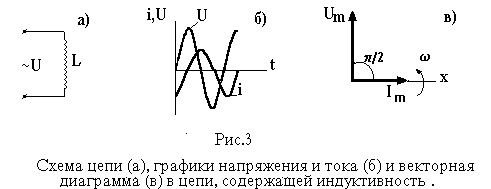
При оценке фазовых соотношений между током и напряжением на индуктивности видно, что ток в цепи, подобно напряжению, имеет синусоидальный характер, но по фазе отстает на угол 2, то есть в момент, когда напряжение на катушке достигает максимума сила тока равна нулю, а в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Графики тока и напряжения, а также векторная диаграмма цепи переменного тока, содержащей индуктивность, представлены на рис . 3 (б, в)_.

Емкость в цепи переменного тока

Рассмотрим цепь переменного тока, в которую включен конденсатор С ( Рис.4а).

Пусть напряжение в цепи изменяется по закону u = U_m sin t. При напряжении U на конденсаторе емкости С заряд на его обкладках будет равен q=CU.

Периодическое изменение U вызывает периодическое изменение q, и возникает емкостный ток:

i=

Продифференцировав это выражение ,получим:

i=CU_m cos t = CU_m sin ( t + /2),

где СU_m=I_m — амплитуда тока.

Cравнивая с законом Ома для участка цепи I_m=U_m/X_C , получаем

СU_m = U_m / X_C , отсюда

X_C = 1 /  C .

Видно, что величина X_C=1/C играет роль сопротивления конденсатора переменному току, она называется емкостным сопротивлением.

Из сравнения фазы тока и напряжения видно, что ток в цепи конденсатора, подобно напряжению, имеет синусоидальный характер, но по фазе опережает напряжение на угол  / 2.

Цепь переменного тока с активным, индуктивным и

емкостным сопротивлениями.

Рассмотрим основные соотношения электрических величин в цепи переменного тока с индуктивностью, емкостью и активным сопротивлением, соединенными последовательно ( Рис .5 а ).

При последовательном соединении проводников, ток, протекающий через сопротивление одинаков

i_L=i_C=i_R=I_m sin t

Полное напряжение цепи будет складываться из падений напряжения на индуктивности, емкости и активном сопротивлении. Составим векторную диаграмму цепи, пользуясь результатами, полученными выше.

В произвольном масштабе отложим вектор амплитуды тока, оди наковый для всех сопротивлений и укажем направление его вращения ( Рис. 5б). Вектор амплитуды напряжения на активном сопротивлении U_mR=I_mR отложим по направлению вектора тока, так как эти величины совпадают по фазе. Вектор амплитуды напряжения на индуктивном сопротивлении U_mL=I_mL отложим вверх под углом /2 к вектору тока I_m , так как это напряжение опережает ток по фазе на угол /2. Вектор амплитуды напряжения на емкости U_mC=I_mC отложим вниз под углом /2 к вектору I_m, так как это напряжение отстает от тока на угол /2. Сложив геометрически векторы U_mL, U_mC и U_mR, получим вектор полного напряжения U_m, приложенного ко всей цепи ( Рис. 5б).

Применив теорему Пифагора, найдем

U_m= = =

=

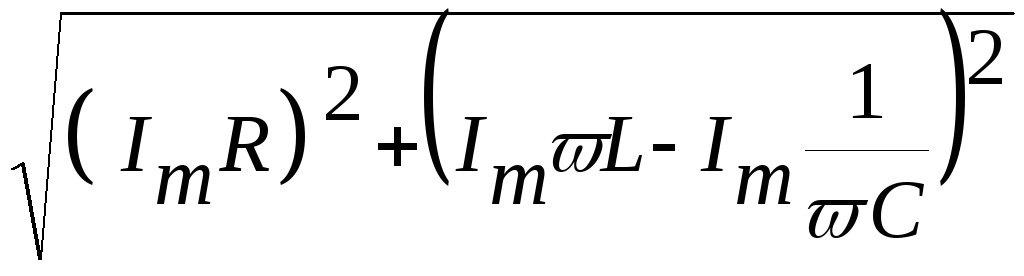Отсюда

I_m=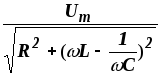

Последняя формула представляет собой закон Ома для полной цепи переменного тока для амплитудных значений. Полным сопротивлением или импедансом цепи называется величина

Z =

Закон Ома справедлив и для мгновенных значений тока и напряжения.

Угол сдвига фаз между током и напряжением ( угол  на рис 5б) может быть определен из соотношений

tg =