ЛАБОРАТОРНАЯ РАБОТА № 1
Определение плотности твердого тела
Приборы и принадлежности: цилиндр, технические весы, разновесы, штангенциркуль
Цель работы: освоить расчет ошибок косвенных измерений на примере определения плотности тела.
ТЕОРИЯ.
Выполнение лабораторных работ связано с измерением различного рода физических величин.
Измерение-это процесс сравнения измеряемой величины с однородной ей величиной, принятой за единицу меры. Вследствие несовершенства наших органов чувств и измерительных приборов измерения выполняются с ограниченной степенью точности, т. е. значение измеряемой величины отличается от истинного.
Под степенью точности прибора понимается та наименьшая часть единицы меры, до которой с уверенностью в правильности результата может быть проведено измерение (например, степень точности школьной линейки 1 мм).
Ошибки (погрешности), возникающие при измерении, делятся на два больших класса: систематические и случайные.
Систематические ошибки- ошибки, сохраняющие свою величину и знак от измерения к измерению. Они связаны с неисправностью прибора, неудачно выбранным методом измерений и т. д. Так как систематические ошибки постоянны, то они не поддаются математическому анализу, но их можно выявить и устранить.
Случайные ошибки- ошибки, которые непредсказуемым образом изменяют свою величину (и знак) от измерения к измерению. Они являются следствием несовершенства наших органов чувств, действия факторов, влияние которых невозможно учесть, и т. д.
Устранить их нельзя, но они подчиняются статистическим закономерностям, их можно рассчитать, используя методы математической статистики.
Величина случайной ошибки существенно уменьшается при увеличении числа измерений.
Измерения делятся на два вида: прямые и косвенные.
Прямые
измерения-
измерения, при которых числовые значения
искомой величины получаются непосредственным
сравнением ее с единицей меры.
Косвенные измерения- измерения, при которых значения искомой величины находятся по результатам измерений других величин, связанных с этой величиной определенной функциональной зависимостью.
Расчет ошибок прямого измерения.
Пусть
проведено n
измерений некоторой величины Х.
В результате получен ряд значений этой
величины:
Наиболее
вероятным является среднее
арифметическое значение
этой величины
:
=
где i=1,2,3,…,n
Величина
называется абсолютной
погрешностью
отдельного
измерения.
Средней
арифметической погрешностью
называют среднее арифметическое значение
абсолютных погрешностей отдельных
измерений:
Средняя
арифметическая
определяет
интервал
,
внутри которого находится истинное
значение измеряемой величины Х.
Качество результата измерений характеризуют средней относительной погрешностью.
Средней
относительной погрешностью
называют отношение средней арифметической
погрешности
к среднему значению измеряемой величины
:
Для
более точного расчета абсолютной
погрешности используют суммарную
погрешность
Суммарная
погрешность
учитывает случайную погрешность
,
погрешность прибора
,
погрешность округления
и определяется соотношением:
,
(1)
где
определяют по формуле Стьюдента:
,
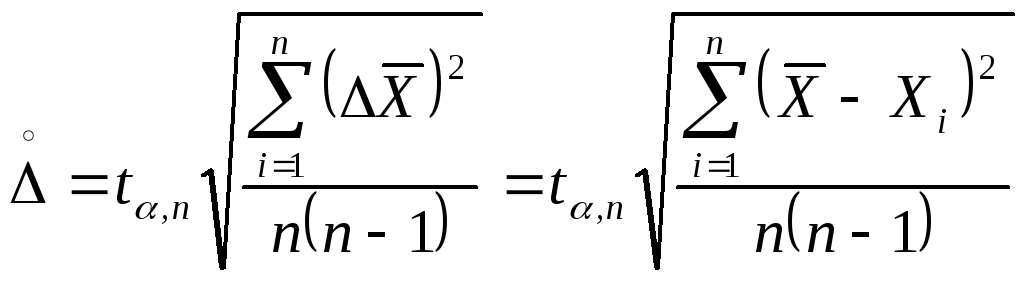t
-
коэффициент Стьюдента (берется из
таблицы Стьюдента),
n- число измерений;
,
где
- предельная ошибка прибора, указанная
в паспорте.
,
где
-
наименьшее
деление прибора.
РАСЧЕТ ОШИБОК КОСВЕННОГО ИЗМЕРЕНИЯ
Пусть искомая величина Z является функцией двух переменных X и Y, т.е
Z=f(x, y).
Установлено, что абсолютная ошибка функции y=f(x) равна произведению производной этой функции на абсолютную ошибку аргумента, т. е.
.
Поэтому для определения абсолютной ошибки функции Z= f(x,y) находят полный дифференциал этой функции:
dz=
, (2)
где
и
-частные производные функции Z
по аргументам X
и Y.
Каждая частная производная находится как простая производная функции Z=f(x,y) по соответствующему аргументу, если оставшийся аргумент рассматривать как постоянный множитель.
При
малых значениях дифференциалов аргументов
dx
и dy
(или приращений аргументов
и
)
приращение функции
.
В
этом случае формула (2) принимает вид:
Z=
.
В
качестве средней абсолютной погрешности
принимают среднюю
квадратичную
погрешность
,которая
определяется соотношением:
,
(3)
где
и
-суммарные
погрешности измерений величины X
и Y,
определяемые по формуле (1).
Средняя
относительная погрешность величины
Z
рассчитывается по формуле
.
Следовательно, разделив обе части
выражения (3) на
,
получим относительную
погрешность функции
Z:
Зная относительную погрешность, находят абсолютную ошибку величины Z:
Окончательный результат измерений записывают так:
Z=
.
Рассмотрим расчет ошибок на примере определения плотности твердого тела правильной геометрической формы.
Для цилиндра массой m, высотой h, диаметром D средняя плотность определяется соотношением:
.
Используя формулу (3), для нашего случая получаем:
.
Найдя
частные производные
имеем:
.
Разделив
левую и правую часть последнего выражения
на
,
получаем:
,отсюда
Таким образом, относительная погрешность плотности
.
Зная
относительную ошибку, находим абсолютную
погрешность плотности (
):
.
Окончательный результат запишем так:
При обработке результатов измерений следует помнить, что точность вычислений должна быть согласована с точностью самих измерений. Например, если хотя бы одна из величин в каком-либо выражении определена с точностью до двух значащих цифр, то нет смысла вести вычисление результата с точностью большей двух значащих цифр. Для уточнения последней значащей цифры результата нужно вычислить следующую за ней цифру: если она окажется меньше 5, то ее следует просто отбросить; если она больше 5 или равна 5,то отбросив ее, следует предыдущую цифру увеличить на единицу.
Вычисление погрешности измерений производят с такой же точностью, что и вычисление самой измеряемой величины.
Например:
Правильно. Неправильно.
Z=
284
Z= 284,5
Z=
52,7
Z=52.74
Z=
4,750
Z=4,75
ОПИСАНИЕ ПРИБОРОВ