
Решение.
Для построения области допустимых значений построим соответствующие данным неравенствам граничные прямые:
 – (I)
– (I)
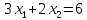 – (II)
– (II)
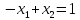 (III)
(III)
по
точкам: для прямой (І)
это
точки
 ,
для прямой (ІI)
это
точки
,
для прямой (ІI)
это
точки
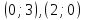 ,,
для прямой (ІІІ):
,,
для прямой (ІІІ):
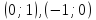 .
.
Определим
полуплоскости, заданные неравенствами.
Для этого подставим координаты точки
О. в неравенства. Если неравенство
удовлетворяется координатами точки
 ,
то неравенства определяет полуплоскости
в которой расположена точка
,
то неравенства определяет полуплоскости
в которой расположена точка
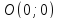 ,
если нет то неравенство определяет
вторую полуплоскость.
Область допустимых решений определяется
как общая часть всех полуплоскостей,
соответствующим четырем данным
неравенствам, и неравенствами
,
если нет то неравенство определяет
вторую полуплоскость.
Область допустимых решений определяется
как общая часть всех полуплоскостей,
соответствующим четырем данным
неравенствам, и неравенствами
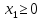 ,
,
 . Это многоугольник
. Это многоугольник
 .
Линии уровня функции
.
Линии уровня функции
 – это семейство параллельных прямых.
Построим одну из них
– это семейство параллельных прямых.
Построим одну из них
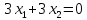 ,
ее вектор нормали
,
ее вектор нормали
 и она проходит через начало координат.
Перемещаем линии уровня линейного
функционала параллельно себе в направлении
вектора
и она проходит через начало координат.
Перемещаем линии уровня линейного
функционала параллельно себе в направлении
вектора
 – значение функции
– значение функции
 возрастает. Наибольшее значение функции
в области допустимых решений принимает
в точке
возрастает. Наибольшее значение функции
в области допустимых решений принимает
в точке
 ,
наименьшее – в точке
,
наименьшее – в точке
 .
.

Найдем
координаты точки
 ,
решив систему уравнений:
,
решив систему уравнений:

Подставим
найденные значения в
 :
:
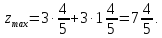
Найдем
координаты точки
 ,
решив систему уравнений:
,
решив систему уравнений:

Подставим
найденные значения в
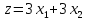 :
:

Ответ.
23.


Решение.
Для построения области допустимых значений построим соответствующие данным неравенствам граничные прямые:
 – (I)
– (I)
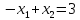 – (II)
– (II)
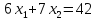 –
(III)
–
(III)
по
точкам: для прямой (І)
это
точки
 ,
для прямой (ІI)
это
точки
,
для прямой (ІI)
это
точки
 ,,
для прямой (ІІІ):
,,
для прямой (ІІІ):
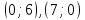 .
.
Определим
полуплоскости, заданные неравенствами.
Для этого подставим координаты точки
О. в неравенства. Если неравенство
удовлетворяется координатами точки
 ,
то неравенства определяет полуплоскости
в которой расположена точка
,
то неравенства определяет полуплоскости
в которой расположена точка
 ,
если нет то неравенство определяет
вторую полуплоскость.
Область допустимых решений определяется
как общая часть всех полуплоскостей,
соответствующим четырем данным
неравенствам, и неравенствами
,
если нет то неравенство определяет
вторую полуплоскость.
Область допустимых решений определяется
как общая часть всех полуплоскостей,
соответствующим четырем данным
неравенствам, и неравенствами
 ,
,
 . Это многоугольник
. Это многоугольник
 .
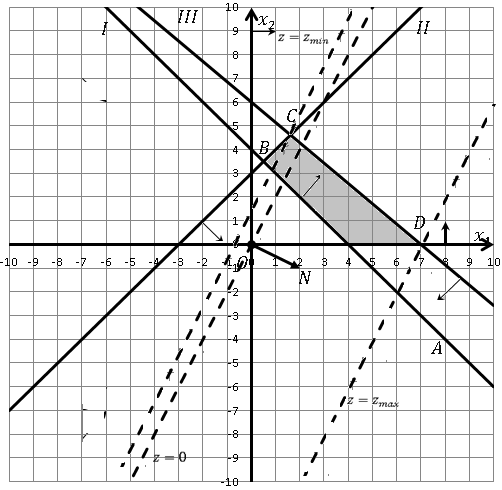
Линии уровня функции
.
Линии уровня функции
 – это семейство параллельных прямых.
Построим одну из них
– это семейство параллельных прямых.
Построим одну из них
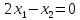 ,
ее вектор нормали
,
ее вектор нормали
 и она проходит через начало координат.
Перемещаем линии уровня линейного
функционала параллельно себе в направлении
вектора
и она проходит через начало координат.
Перемещаем линии уровня линейного
функционала параллельно себе в направлении
вектора
 – значение функции
– значение функции
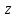 возрастает. Наибольшее значение функции
в области допустимых решений принимает
в точке
возрастает. Наибольшее значение функции
в области допустимых решений принимает
в точке
 ,
наименьшее – в точке
,
наименьшее – в точке
 .
.
Найдем
координаты точки
 ,
решив систему уравнений:
,
решив систему уравнений:

Подставим
найденные значения в
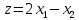 :
:

Найдем
координаты точки
 ,
решив систему уравнений:
,
решив систему уравнений:
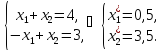
Подставим
найденные значения в
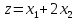 :
:

24.


Решение.
Для построения области допустимых значений построим соответствующие данным неравенствам граничные прямые:
 –
(I)
–
(I)
 – (II)
– (II)
 –
(III)
–
(III)
по
точкам: для прямой (І)
это
точки
 ,
для прямой (ІI)
это
точки
,
для прямой (ІI)
это
точки
 ,,
для прямой (ІІІ):
,,
для прямой (ІІІ):
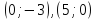 .
.
Определим
полуплоскости, заданные неравенствами.
Для этого подставим координаты точки
О. в неравенства. Если неравенство
удовлетворяется координатами точки
 ,
то неравенства определяет полуплоскости
в которой расположена точка
,
то неравенства определяет полуплоскости
в которой расположена точка
 ,
если нет то неравенство определяет
вторую полуплоскость.
Область допустимых решений определяется
как общая часть всех полуплоскостей,
соответствующим четырем данным
неравенствам, и неравенствами
,
если нет то неравенство определяет
вторую полуплоскость.
Область допустимых решений определяется
как общая часть всех полуплоскостей,
соответствующим четырем данным
неравенствам, и неравенствами
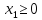 ,
,
 . Это многоугольник
. Это многоугольник
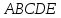 .
Линии уровня функции
.
Линии уровня функции
 – это семейство параллельных прямых.
Построим одну из них
– это семейство параллельных прямых.
Построим одну из них
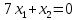 ,
ее вектор нормали
,
ее вектор нормали
 и она проходит через начало координат.
Перемещаем линии уровня линейного
функционала параллельно себе в направлении
вектора
и она проходит через начало координат.
Перемещаем линии уровня линейного
функционала параллельно себе в направлении
вектора
 – значение функции
– значение функции
 возрастает. Наибольшее значение функции
в области допустимых решений принимает
в точке
возрастает. Наибольшее значение функции
в области допустимых решений принимает
в точке
 ,
наименьшее – в точке
,
наименьшее – в точке
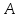 .
.
Найдем
координаты точки
 ,
решив систему уравнений:
,
решив систему уравнений:

Подставим
найденные значения в
 :
:

Найдем
координаты точки
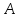 ,
решив систему уравнений:
,
решив систему уравнений:

Подставим
найденные значения в
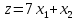 :
:

28.


