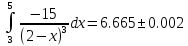laba_4
.docxАвтономное образовательное учреждение
высшего профессионального образования Ленинградской области
Государственный институт экономики, финансов, права и технологий
Кафедра информационных технологий и высшей математики
Дисциплина «Использование Mathcad для решения экономических задач »
Лабораторная работа №4
на тему
«Численное интегрирование»
Выполнила студентка
3 курса
123 группы
Янченко В.А.
Проверил:
Алексеев Г.В.
Гатчина
2014
Цель работы: ознакомиться с численными методами вычисления определённых интегралов, научиться решать задачи с использованием формулы Симпсона, трапеций, правых и левых прямоугольников, метода Монте-Карло и оценивать погрешность всех перечисленных формул.
Задача №1: Метод прямоугольников
Вычислить
приближенное значение интеграла функции
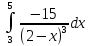
на отрезке [3;5] , используя формулы левых и правых прямоугольников, при n=1000.
Ход работы:
-
Задаем функцию f(x), отрезок [a,b] и функцию нахождения дифференциалов n-го порядка.
В
нашем случае: функция
 ,
а отрезок [3;5].
,
а отрезок [3;5].
-
Находим значение интеграла заданной функции для использования его в дальнейшем решении.
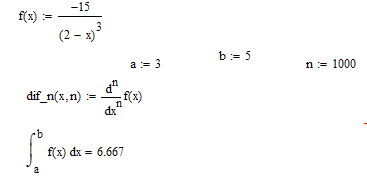
Составим функцию , входными параметрами которой являются : a,b- левая и правая границы интервала ; n- количество разбиений ; char- если имеет значение ”left’’, то идет подсчет по формуле левых прямоугольников , любое другое - по формуле правых прямоугольников.
Погрешность показывает, что полученное значение интеграла верно до третьего знака после запятой.
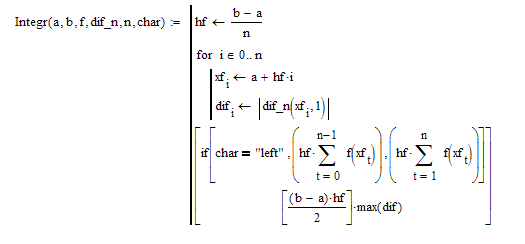
Integr(a,b,n,’’left’’)=
Integr(a,b,n,’’right’’)=
Ответ:
приближенное значение интеграла
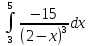 =6.669
=6.669 по формуле левых прямоугольников, и
по формуле левых прямоугольников, и
 -
по формуле правых прямоугольников.
-
по формуле правых прямоугольников.
Задача
№2:
Вычислить приближенное значение
интеграла функции
 используя общую формулу Симпсона, при
n=1000.
используя общую формулу Симпсона, при
n=1000.
Ход работы:
Составим функцию , входными параметрами которой являются : a,b- левая и правая границы интервала ; n- количество разбиений. Индексы iEven и iUneven обозначают четность и нечетность соответственно.
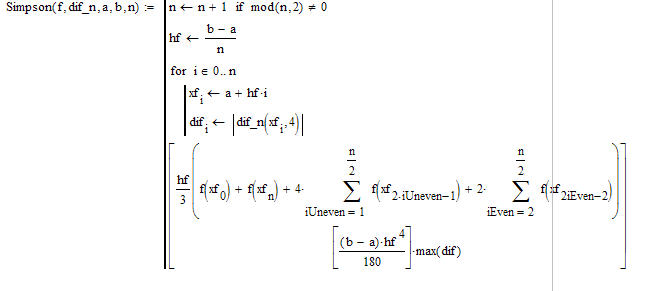
Simpson(a,b,n)=
Следовательно, решением будет число, равное 6.667. Погрешность показывает, что полученное значение интеграла верно до третьего знака.
Ответ:
значение
интеграла
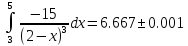
Задача
№3:
Вычислить приближенное значение
интеграла функции
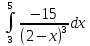 используя формулу трапеций, при n=1000.
используя формулу трапеций, при n=1000.
Ход работы:
Введем функцию, реализующую вычисление интеграла методом трапеций.

Trapes(a,b,n)=
Ответ:
значение интеграла
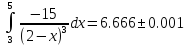
Задача
№4:
Вычислить приближенное значение
интеграла функции
 используя метод Монте-Карло, при n=1000.
используя метод Монте-Карло, при n=1000.
Ход работы:

i:=0..n


I=6.665
Ответ:
значение интеграла