4. Щільність ентропії стаціонарного ддп

Нехай розглядається стаціонарний ДДП з деяким алфавітом 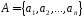, що породжує (генерує)-символьні випадкові повідомлення. Дослідимо асимптотичну поведінку ентропіїпри.

Оскільки ДДП є стаціонарним, то -вимірний дискретний розподіл ймовірностей

, .

не змінюється при зсуві початку відліку часу:

.

В силу цього ентропія -символьного "зсунутого" повідомленняне залежить від:

.

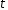Тому надалі можна не розрізняти випадкові повідомлення і.

Означення. Щільністю ентропії стаціонарного ДДП називається границя

. (5)

якщо вона існує.

За означенням є ентропією, що доводиться на один символ і обчислену за нескінченно довгим випадковим повідомленням. Якщо, то із збільшенням довжини повідомленняентропія зростає лінійно:

.

З'ясуємо умови існування границі в (5), тобто асимптотичної поведінки ентропії.

Нехай і– випадкові повідомлення довжиниівідповідно,– символ конкатенації. Позначимо черезумовну ентропію символувідносно випадкового повідомлення, яке складається зпопередніх символів,:

.

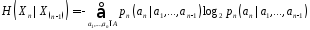У випадку покладають.

Теорема 1. Для довільного стаціонарного ДДП числова послідовність умовних ентропій ,, має скінченну границю:

.

Теорема 2. Для довільного стаціонарного ДДП щільність ентропії існує і збігається з граничним значенням (5):

.

Теорема 3. Для ентропії довільної дискретної стаціонарної послідовності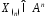при збільшенні числа символів справедлива асимптотична рівність

, (6)

де

.

В асимптотичній формулі (6) – це-кратна щільність ентропії,– це ентропія, обумовлена граничними ефектами.

Наслідок. Для довільного стаціонарного ДДП без пам’яті асимптотична рівність (6) перетворюється на точну рівність

,

де

–

ентропія одиничного випадкового символу.

4. Однорідний ланцюг Маркова як модель джерела дискретних повідомлень

В системах обробки і захисту інформації символи, що утворюють повідомлення звичайно стохастично залежні. Одною з поширених моделей стохастичної залежності символів друкарських текстів, мовних повідомлень і зображень є однорідний ланцюг Маркова (ОЛМ) з дискретним часом і простором станів,.

Нехай випадкова символьна послідовність, породжена джерелом дискретних повідомлень, є однорідним ланцюгом Маркова. Це означає, що розподіл ймовірностей майбутніх значень (станів) при фіксованих теперішніх і минулих значеннях не залежить від минулих значень:

,

, . Відомо також, що усі скінченновимірні розподіли і всі ймовірнісні характеристики ОЛМ повністю виражаються через вектор початкових ймовірностей

, , , .

і через -матрицю ймовірностей переходу за один крок:

, ,,

Позначимо через , , вектор граничних ймовірностей (стаціонарний розподіл), який є розв’язком системи лінійних алгебраїчних рівнянь:

а через

–

ентропію стаціонарного розподілу ймовірностей;

.

Теорема (про ентропію ОЛМ). Якщо випадкова символьна послідовність є ОЛМ із стаціонарним початковим розподілом іматрицею ймовірностей переходу за один крок, то ентропія повідомленнязсимволів дорівнює

.

Наслідок. В умовах теореми про ентропію ОЛМ асимптотична рівність (6) перетворюється на точну рівність

, (6)

де

.