
- •Лекція № 10 Тема: Біноміальний, рівномірний і нормальний розподіл ймовірностей
- •1. Біноміальний розподіл ймовірностей
- •1.1. Розподіл Бернуллі
- •2. Рівномірний розподіл
- •2.1 Рівномірний дискретний розподіл
- •2.2 Рівномірний неперервний розподіл
- •3. Нормальний розподіл ймовірностей
- •4. Нормальне наближення
- •5. Розподіли, пов’язані з нормальним
- •1) Розподіл 2 (хі-квадрат)
- •2) Розподіл Стьюдента (-розподіл)
- •6. Оцінки параметрів розподілу випадкових величин
- •7. Оцінки параметрів біноміального розподілу
- •8. Оцінки параметрів нормального розподілу
- •8.1 Довірчий інтервал для математичного сподівання при відомій дисперсії
- •8.2 Довірчий інтервал для математичного сподівання при невідомій дисперсії
- •8.3. Довірчий інтервал для дисперсії при відомому математичному сподіванні
- •8.4. Довірчий інтервал для дисперсії при невідомому математичному сподіванні
- •8.5. Довірчий інтервал для середнього квадратичного відхилення
8.3. Довірчий інтервал для дисперсії при відомому математичному сподіванні
Нехай
 – вибірка спостережень з нормальної
генеральної сукупності. Знайдемо
довірчий інтервал для дисперсії
– вибірка спостережень з нормальної
генеральної сукупності. Знайдемо
довірчий інтервал для дисперсії нормально розподіленої величини
нормально розподіленої величини з відомими математичним сподіванням
з відомими математичним сподіванням .
.
Оскільки
значення математичного сподівання
відоме, то як оцінку величини
 візьмемо точкову оцінку дисперсії
візьмемо точкову оцінку дисперсії ,
яку будемо розглядати як випадкову
величину, залежну від випадкової вибірки.
Тоді величина
,
яку будемо розглядати як випадкову
величину, залежну від випадкової вибірки.
Тоді величина є сумою квадратів значень
є сумою квадратів значень .
Ці величини мають стандартний нормальний
розподіл з параметрами 0 і 1, а сума
.
Ці величини мають стандартний нормальний
розподіл з параметрами 0 і 1, а сума має
має розподіл Пірсона з
розподіл Пірсона з степенями вільності. Користуючись
щільністю
степенями вільності. Користуючись
щільністю -розподілу,
знайдемо інтервал, в який значення
-розподілу,
знайдемо інтервал, в який значення потрапляють з надійністю
потрапляють з надійністю .
Позначимо цей інтервал
.
Позначимо цей інтервал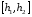 .
Оскільки розподіл
.
Оскільки розподіл не є симетричним, то щоб отримати
симетричний відносно параметра інтервал,
значення
не є симетричним, то щоб отримати
симетричний відносно параметра інтервал,
значення і
і виберемо так, щоб ймовірність попадання
значень
виберемо так, щоб ймовірність попадання
значень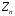 лівіше
лівіше і правіше
і правіше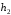 була однаково рівною
була однаково рівною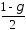 .
Тоді
.
Тоді
 .
.
Числа
 і
і
 можна
відшукати за спеціальною таблицею
критичних точок розподілу
можна
відшукати за спеціальною таблицею
критичних точок розподілу
 ,
виходячи з того, що
,
виходячи з того, що
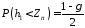 ,
, .
Після того, як числа
.
Після того, як числа і
і
 вибрані,
можливо визначити довірчий інтервал
для дисперсії
вибрані,
можливо визначити довірчий інтервал
для дисперсії
 .
Оскільки
.
Оскільки ,
то нерівність
,
то нерівність перетвориться на нерівність
перетвориться на нерівність або, в еквівалентному вигляді
або, в еквівалентному вигляді .
Цяподвійна
нерівність означає,
що довірчим інтервалом для дисперсії
.
Цяподвійна
нерівність означає,
що довірчим інтервалом для дисперсії
 з надійністю
з надійністю є проміжок
є проміжок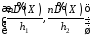 .
.
Зауваження.
Таблиці критичних точок
 і
і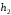 розподілу
розподілу містять два параметри: рівень значущості
містять два параметри: рівень значущості ,
визначуваний значеннями
,
визначуваний значеннями і
і ,
а також число степенів свободи, рівне
об'єму вибірки
,
а також число степенів свободи, рівне
об'єму вибірки .
Критичні значення в таблицях найчастіше
позначаються
.
Критичні значення в таблицях найчастіше
позначаються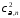 .
.
Зауваження.
Критичні
точки розподілу
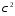 можна
обчислити
можна
обчислити
а) в Excel за формулою =ХИ2ОБР(α; k), де α – рівень значущості, k – число ступенів свободи.
а) в Mathcad за формулою qchisq(1–α; k), де α – рівень значущості, k – число ступенів свободи.
Приклад
4.
В умовах прикладу 3 знайти довірчий
інтервал для дисперсії з
надійністю
з
надійністю
 .
.
Розв’язання.
Об'єм вибірки
 ,
вибіркове середнє
,
вибіркове середнє ,
вибіркова дисперсія
,
вибіркова дисперсія .
За
заданою надійністю
.
За
заданою надійністю
 обчислимо
обчислимо
 ,
,
 .
.
Відшукаємо
числа
 і
і
 за
таблицею критичних точок розподілу
за
таблицею критичних точок розподілу
 :
:
 ,
,
 .
.
Отримаємо довірчий інтервал для дисперсії:
 ,
,
 .
.
Таким
чином, інтервал
 покриває параметр
покриває параметр з надійністю
з надійністю привідомому
математичному сподіванні.
привідомому
математичному сподіванні.
8.4. Довірчий інтервал для дисперсії при невідомому математичному сподіванні
Знайдемо
довірчий інтервал для дисперсії
 нормально розподіленої величини
нормально розподіленої величини з невідомими математичним сподіванням.При
виведенні інтервальної оцінки у разі
відомого математичного сподівання
,
ми користувалися величиною
з невідомими математичним сподіванням.При
виведенні інтервальної оцінки у разі
відомого математичного сподівання
,
ми користувалися величиною
 .
Тепер це значення використовувати
неможна, тому за незміщену оцінку
дисперсії будемо використовувати
виправлену вибіркову дисперсію
.
Тепер це значення використовувати
неможна, тому за незміщену оцінку
дисперсії будемо використовувати
виправлену вибіркову дисперсію ..
Випадкова величина
..
Випадкова величина має розподіл Пірсона
має розподіл Пірсона із
із ступенями свободи. Виберемо близьку
до одиниці ймовірність
ступенями свободи. Виберемо близьку
до одиниці ймовірність і знайдемо інтервал, в який потрапляє
невідомий параметр з надійністю
і знайдемо інтервал, в який потрапляє
невідомий параметр з надійністю .
Для цього повторимо міркування пункту
8.3 і отримаємо, що оцінюване значення
дисперсії
.
Для цього повторимо міркування пункту
8.3 і отримаємо, що оцінюване значення
дисперсії з надійністю
з надійністю покривається довірчим інтервалом
покривається довірчим інтервалом
 .
.
Приклад
5.
В умовах прикладу 3 знайти довірчий
інтервал для дисперсії при
невідомому
математичному сподіванні
з надійністю
при
невідомому
математичному сподіванні
з надійністю
 .
.
Розв’язання.
Об'єм вибірки
 ,
вибіркове середнє
,
вибіркове середнє ,
вибіркова дисперсія
,
вибіркова дисперсія ,
виправлена вибіркова
дисперсія
,
виправлена вибіркова
дисперсія
 .
.
Отримаємо довірчий інтервал для дисперсії:
 ,
,
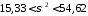 .
.
Таким
чином, інтервал
 покриває параметр
покриває параметр з надійністю
з надійністю при невідомому
математичному сподіванні.
при невідомому
математичному сподіванні.
