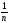2. Рівномірний розподіл

2.1 Рівномірний дискретний розподіл

Означення. Дискретна випадкова величина називаєтьсярівномірно розподіленою, якщо вона набуває значеньз ймовірностями ,.

Закон розподілу:

	1	2	3	...
				...

Функція розподілу:

Числові характеристики:

, .

2.2 Рівномірний неперервний розподіл

Означення. Неперервна випадкова величина 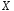називається рівномірно розподіленою на відрізку, якщо її щільність ймовірності є сталою наі дорівнює 0 поза ним:

Графік функції має вид:

Рівномірний розподіл виникає в експериментах, у яких навмання ставиться точка на відрізку (випадкова величина– абсциса поставленої точки), а також в експериментах по вимірюванню тих чи інших фізичних величин з округленням (випадкова величина– помилка округлення). Наприклад:– час чекання на зупинці автобуса:розподілена рівномірно на відрізку, де– інтервал руху автобусів. Інший приклад:– помилка при зважуванні предмета, яка отримана від округлення результату зважування до найближчого цілого числа; у цьому випадку випадкова величинамає рівномірний розподіл на відрізку, де за одиницю прийнята ціна розподілу шкали.

Функція розподілу:

Числові характеристики:

, ,.

3. Нормальний розподіл ймовірностей

Означення. Неперервна випадкова величина називається розподіленою за нормальним законом (законом Гаусса) з параметрамиі, де,, якщо її щільність ймовірності має вигляд:

,

Нормальний розподіл було відкрито в 1733 році А. Муавром, а потім докладно вивчено П. Лапласом і К. Гауссом.

Позначається нормальний розподіл .

Якщо випадкова величина 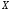розподілена за нормальним закономз параметрами 0 і 1, то вона називається нормованою або стандартною нормальною випадковою величиною. Щільність стандартного нормального розподілу є функцією Гаусса:

.

Зауваження. Для значень функції Гаусса існують детальні таблиці.

Значення функції Гаусса можна обчислити

а) в Excel за формулою =НОРМРАСП(х; 0;1;ЛОЖЬ).

а) в Mathcad за формулою dnorm(x,0,1).

Графік щільності нормального розподілу називається нормальною кривою (кривою Гаусса) і має наступний симетричний вигляд, схожий на дзвін; залежний від різних значень параметра :

Максимальна висота дзвону досягається при та дорівнює

,

При збільшенні параметра вершина дзвону буде опускатися, але зате будуть підніматися краї (тому що загальна площа між графіком і віссюповинна залишитися рівною 1). Що стосується параметра, то його значення не впливає на форму графіка; зі зміноюграфік тільки зміщується в напрямку осі.

Нормальний закон – це закон розподілу, що найчастіше зустрічається на практиці. Він широко розповсюджений у природі, техніці виробництві, і т. ін.. Випадковими величинами з нормальним законом розподілу є, наприклад, погрішності вимірювань фізичних величин, та й самі результати вимірювань; координати точки падіння снаряда під час стрілянини з гармати при постійному прицілі й ін.

Функція розподілу:

.

Функція розподілу нормальної випадкової величини зв'язана з функцією Лапласа наступним співвідношенням:

.

Зауваження. Для значень функції розподілу нормальної випадкової величини існують детальні таблиці.

Значення функції цієї функції можна обчислити

а) в Excel за формулою =НОРМРАСП(х; 0;1;ИСТИНА)–0,5 або за формулою =НОРМСТРАСП(х)–0,5.

а) в Mathcad за формулою pnorm(x,0,1)–0,5.

Ймовірність того, що нормально розподілена випадкова величина набуває значень з деякого проміжку

.

Якщо покласти ,, то

,

тобто подія є практично достовірною. Це означає, що практично всі можливі значення нормально розподіленої випадкової величини розташовані на проміжку. Останнє твердження називають "правилом трьох сигм".

Числові характеристики нормального розподілу збігаються з його параметрами:

, ,.

Нормальний розподіл має широке розповсюдження в прикладних задачах. Це пов’язано з тим, що багато з випадкових величин, які досліджуються, є наслідками різних випадкових подій. Зокрема, при достатньо загальних припущеннях сума великого числа незалежних випадкових величин має розподіл, близький до нормального.