Алгебраїчні дії над матрицями

До лінійних операцій над матрицями відносяться наступні.

1) Множення матриці на число:

k∙А=(k∙а_ij), (1)

тобто кожний елемент матриці множиться на це число;

2) алгебраїчна сума матриць однакової розмірності:

А±В=(а_ij±в_ij), (2)

тобто відповідні елементи матриць додаються або віднімаються.

Множення матриць є нелінійною операцією. Добуток АВ матриць А та В існує лише при виконанні умов узгодженості: кількість стовпців матриці А (першого множника) дорівнює кількості рядків матриці В (другого множника).

Добутком АВ матриці А розмірності mхр і матриці В розмірності рхn є матриця С розмірності mхn, елементи якої с_ij дорівнюють сумі добутків елементів i–того рядка матриці А на відповідні елементи j–го стовпця матриці В

с_ij = а_i1в_1j+ а_i2в_2j+ а_i3в_3j+…+а_inв_рj, (3)

тобто елемент с_ij отримують за схемою:

Зауваження 1. Загалом добуток матриці не має властивості комутативності, тобто АВ≠ВА. В окремих випадках добуток матриць не залежить від порядку множників. Наприклад, якщо А – квадратна матриця порядку n, Е – одинична матриця порядку n, тоді АЕ=ЕА=А.

Приклад 2. Знайти добуток матриць

, .

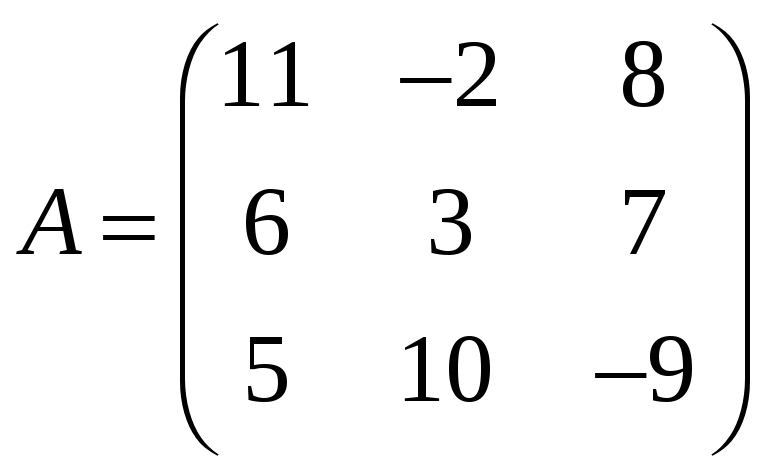Розмірності: 3х3 3х4

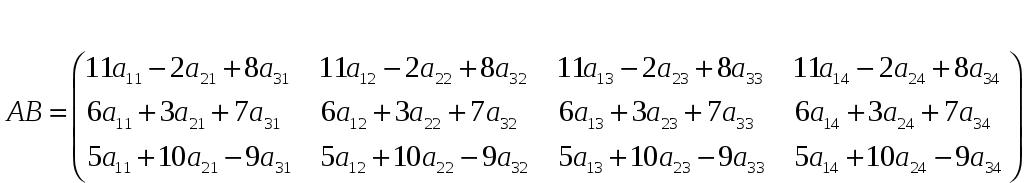
Розмірність: 3х4

Зазначимо: добуток ВА не існує – не виконується умова узгодженості.

Властивості алгебраїчних операцій над матрицями

1. А+В=В+А (комутативність суми)

2. k∙(А+В)=k∙А+k∙В, де k – числовий множник

3. А+(В+С)=(А+В)+С (сполучний закон додавання)

4. А∙(ВС)=(АВ)∙С (сполучний закон множення)

5. А∙(В+С)=А∙В+А∙С (розподільний закон)

6. А+0=А, де 0 – нульова матриця однакової розмірності із матрицею А.

7. А∙Е=А, Е∙А=А, де одиничні матриці Е задовольняють умові узгодженості з матрицею А і будуть різного порядку для неквадратної матриці А.

Зауваження 2. Якщо добуток матриць є нульова матриця, то необов'язковим є те, що серед матриць-співмножників є нульова матриця. Справді,

.

2. Визначники 2-го та 3-го порядку.

Означення 2. Визначником n–го порядку квадратної матриці А порядку n називають величину (число, якщо елементи матриці – числа), що знаходиться з елементів матриці А за певним правилом. Визначник позначається (А) чи або det(A) (детермінант матриці А). В розгорненому вигляді визначник позначають, вказуючи між двома вертикальними відрізками таблицю усіх елементів матриці А (на відміну від позначення матриці А, таблицю елементів якої вказують в круглих чи квадратних дужках).

Правило обчислення визначника 2-го порядку

Для знаходження визначника 2-го порядку потрібно від добутку елементів головної діагоналі матриці відняти добуток елементів побічної діагоналі, тобто

(4)

Правило обчислення визначника 3-го порядку

Визначник 3-го порядку знаходиться за формулою

(5)

.

Для запам’ятовування правила обчислення визначника третього порядку застосовують таку схему (правило трикутників):

Позначимо точками елементи визначника, тоді доданки зі знаком «плюс» у формулі (5) – це добутки елементів a₁₁, a₂₂, a₃₃, розміщених на головній діагоналі визначника, та добутки елементів a₁₃, a₂₁, a₃₂ і a₁₂, a₂₃, a₃₁, розміщених у вершинах рівнобедрених трикутників, основи яких паралельні головній діагоналі. Зі знаком «мінус» беруться доданки, що є добутками елементів a₁₃, a₂₂, a₃₁, розміщених на побічній діагоналі визначника, та у вершинах трикутників, основи яких паралельні побічній діагоналі визначника — a₁₁, a₂₃, a₃₂ і a₁₂, a₂₁, a₃₃.

Розклад визначника вищого порядку за елементами рядка (стовпця)

Для обчислення визначників порядку n>3, а також і порядку n=3 (додатково до зазначеного вище правила), використовують поняття алгебраїчного доповнення.

Означення 3. Мінором М_ij елемента а_ij визначника n-го порядку називається визначник (n-1)-го порядку, який одержують із визначника (А) шляхом викреслювання i-того рядка та j-того стовпця, на перетині яких знаходиться цей елемент.

Означення 4. Алгебраїчним доповненням А_ij елемента а_ij визначника називають мінор цього елемента, взятий зі знаком «плюс», якщо сума індексів (i+j) парна, та зі знаком «мінус», якщо сума індексів (i+j) непарна, тобто

А_ij =(-1)^i+j∙M_ij (6)

Правило обчислення визначника n-го порядку

Визначник n-го порядку дорівнює сумі добутків елементів будь-якого рядка (або стовпця) на відповідні алгебраїчні доповнення цих елементів.

У випадку використання i-того рядка це правило записується так:

_ij (7)

Формула (7) виражає розклад визначника за елементами i-того рядка.

Зауваження 3. Обчислення визначника n-го порядку зводиться до обчислення n визначників (n-1)-го порядку кожен. Тому визначник доцільно розкладати за елементами а_ij того рядка (стовпця), який містить якомога більшу кількість нулів.