
- •Завдання на самостійну роботу
- •Вступ. Зміст та задачі дискретної математики
- •1. Поняття множини. Способи задання множини
- •2. Способи задання множин
- •3. Відношення між множинами. Геометричне зображення множин
- •3. Основні операції над множинами
- •4. Властивості операцій над множинами
- •5. Декартовий добуток множин
3. Основні операції над множинами
Існує
ще один спосіб задання множин – за
допомогою операцій над іншими множинами.
На булеані
![]() визначаються наступні операції над
множинами
визначаються наступні операції над
множинами
![]() і
і
![]() .
.
|
Назва і позначення |
Означення |
Геометрична ілюстрація |
|
Об'єднання
|
|
|
|
Переріз
|
|
|
|
Різниця
|
|
|
|
Доповнення
|
|
|
|
Симетрична різниця
|
|
|
Використовуючи
операції ∩¸
![]() ¸
\¸
¸
\¸
![]() можна виражати одні множини через інші.
За
умовчанням приймається пріоритет
операцій:
можна виражати одні множини через інші.
За
умовчанням приймається пріоритет
операцій:
![]() .
Для зміни цього порядку у виразі
використовують дужки.
.
Для зміни цього порядку у виразі
використовують дужки.
Таким чином, множину можна задати виразом, в який входять множини, операції і, може бути, дужки. Такий спосіб завдання множини називається аналітичним.
4. Властивості операцій над множинами
Операції
над множинами, як і операції над числами,
мають певні властивості. Ці властивості
виражаються сукупністю тотожностей
незалежно від конкретного змісту множин,
що входять у них, і є підмножинами деякого
універсуму
![]() ,
тобто множинами з
,
тобто множинами з
![]() .
.
Теорема.
Для
будь-яких множин
![]() з булеану
з булеану
![]() справедливі наступні тотожності (основні
закони теорії множин):
справедливі наступні тотожності (основні
закони теорії множин):
|
1.
|
1*.
|
|
2.
асоціативність
|
2*. |
|
3.
|
3*.
|
|
закони поглинання |
|
|
4.
|
4*.
|
|
закони де Моргана |
|
|
5.
|
5*.
|
|
6.
|
|
|
закони ідемпотентності |
|
|
7.
|
7*.
|
|
властивості
|
|
|
8.
|
8*.
|
|
9.
|
9*.
|
|
10.
|
|
|
11.
|
|
|
12.
|
|
Доведення (самостійно) всіх рівносильностей проводиться
1) за означенням рівності множин і за означеннями операцій над множинами.
2) за допомогою діаграм Ейлера-Венна.
За допомогою основних властивостей операцій над множинами доводять рівності множин і спрощують вирази алгебри множин.
5. Декартовий добуток множин
Нехай
![]() і
і
![]() – довільні множини.
– довільні множини.
Означення.
Впорядкованою
парою
називається пара
![]() елементів
елементів
![]() ,
,
![]() ,
взятих в певному порядку.
,
взятих в певному порядку.
Дві впорядковані пари вважаються рівними, якщо рівні їх відповідні компоненти:
![]() .
.
Означення.
Декартовим
добутком двох
множин
![]() і
і
![]() називається
множина всіх впорядкованих пар
називається
множина всіх впорядкованих пар
![]() :
:
![]() .
.
Якщо
![]() ,
то кажуть про декартовий
квадрат множини
,
то кажуть про декартовий
квадрат множини
![]() :
:
![]()
Аналогічно
можна ввести декартовий добуток трьох
![]() ,
чотирьох
,
чотирьох
![]() і т.д. множин. При
і т.д. множин. При
![]() скорочено
пишуть
скорочено
пишуть
 і кажуть про
і кажуть про
![]() -й
декартовий степінь множини
-й
декартовий степінь множини
![]() .
Елементами
.
Елементами
![]() є послідовності (набори, вектори, рядки)
є послідовності (набори, вектори, рядки)
![]() довжини
довжини
![]() .
.
За
означенням покладають, що перший
декартовий степінь будь-якої множини
![]() є сама множина
є сама множина
![]() ,
тобто
,
тобто
![]() .
.
Декартовий добуток має наступні властивості:
-
 – некомутативність;
– некомутативність; -
 – дистрибутивність
відносно
– дистрибутивність
відносно
 ;
; -
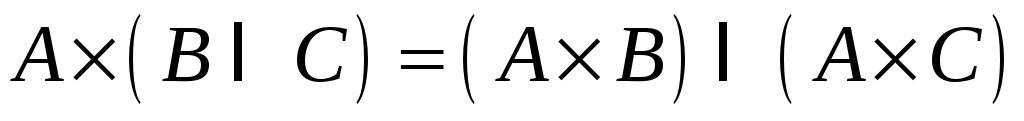 – дистрибутивність
відносно
– дистрибутивність
відносно
 ;
; -
 .
.
Приклад:
Нехай
![]() ,
,
![]() .
Тоді
.
Тоді
![]() ;
;
![]() .
.
2. Нехай
R
– множина всіх
дійсних чисел.
Тоді декартовий квадрат
![]() є
просто множина
всіх
декартових координат на площині відносно
заданих координатних осей (
– множина точок площини).
Якщо
є
просто множина
всіх
декартових координат на площині відносно
заданих координатних осей (
– множина точок площини).
Якщо
![]() ,
то
,
то
![]() – одиничний квадрат на площині.
– одиничний квадрат на площині.
Лекція розроблена доцентом кафедри ВМ, к.т.н. Скубаком О.М.






