3. Контрольні запитання.

1 Що характеризує тангенціальне й нормальне прискорення?

2 Як пов'язані лінійні й кутові характеристики руху?

3 Що називають плечем сили?

4 Що називається моментом сили відносні осі?

5 Що таке момент інерції матеріальної точки?

6 Що являє собою момент інерції тіла?

7 Від чого залежить момент інерції тіла?

8 Яке тіло називається абсолютно твердим?

9 Який рух називається обертальним?

10 У чому полягає основний закон динаміки обертального руху?

4. Домашнє завдання

для виконання роботи треба вивчити наступні питання:

- лінійна та кутова швидкості;

- тангенціальне, нормальне, повне й кутове прискорення;

- момент сили відносно осі обертання;

- момент інерції матеріальної точки та АТТ відносно осі обертання;

- основний закон динаміки обертального руху.

5. Лабораторне завдання.

Установка (рис. 4) складається з насаджених на одну вісь шківа діаметром d і диска, на якому закріплюється досліджуване тіло. На шків намотана нитка, до кінця якої прикріплений тягарець масою . Якщо нитку перекинути через блок і дати їй можливість прискорено опускатися, то шків, диск і досліджуване тіло набудуть обертального руху.

Рис. 4.

При прискореному русі тягарця вниз сила натягу нитки буде

, (23)

де a- лінійне прискорення вантажу, чисельно рівне тангенціальному прискоренню точок поверхні шківа, з якого змотується нитка; g – прискорення вільного падіння ().

Сила, що створює обертальний момент чисельно рівна, але протилежно напрямлена до сили натягу та прикладена до ободу шківа. Плечем цієї сили є половина діаметра шківа (радіус шківа). Отже, обертальний момент

(24)

Якщо врахувати, що пройдений прискорено падаючим тягарцем шлях

, то

, (25)

а кутове прискорення частин, які обертаються, на підставі формули (15) буде:

(26)

Обертальний момент з врахуванням співвідношення (24) виразиться так:

У цьому виразі величина , тому можна вважати, що

(27)

З основного закону динаміки обертального руху (22)

,

а якщо підставити вирази (22) і (27), то розрахункова формула для визначення моменту інерції I для даного положення досліджуваного тіла матиме вигляд:

(28)

6. Порядок виконання роботи:

1. Виміряти штангенциркулем діаметр шківа d.

2. Намотати нитку з тягарцем () на шків, пропустити через блок.

3. Розташувати тіло на платформі в одному з трьох різних положень, відпустити тягарець та виміряти шлях пройдений тягарцем і час проходження цього шляху.

4. Дослід проробити 3 рази та знайти середнє арифметичне значення часу .

5. Змінити розташування досліджуваного тіла та провести ще дві серії вимірювань (для двох різних положень тіла, що залишились).

6. Зняти тіло з платформи і проробити ті ж вимірювання.

7. Для кожного досліду обчислити:

• величину I за формулою (28);

• відносну похибку непрямих вимірювань за формулою:

, ,

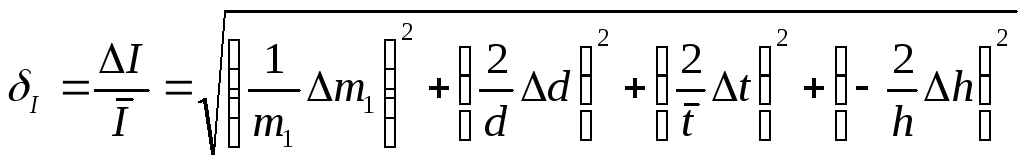де m₁, d, , h – маса тягарця, діаметр шківа, середній час опускання тягарця та шлях тягарця відповідно, а , , , - абсолютні похибки прямих вимірювань маси, діаметру шківа, часу та пройденого шляху відповідно.

- абсолютну похибку непрямого вимірювання за формулою: .

8. Результати вимірювань і обчислень записати в таблицю 1.

Примітка: Маса падаючого вантажу () та маса тіла, момент інерції якого досліджується (), зазначені безпосередньо на них, та визначені з похибкою

Таблиця 1

№ досліду	Положення тіла	m1, кг	d, м	h, м	с	, с
1	І положення
2
3
4	ІІ положення
5
6
7	ІІІ положення
8
9

9. Для кожного з положень тіла результати розрахунків записати у вигляді:

кгм², при =…%

У висновку порівняти знайдені дослідним шляхом моменти інерції тіла з обчисленими за формулою (21).