
Matematicheskaya_statistika_v_meditsine
.pdf
P A = P A + A + A A + A |
= P A |
+ P A |
|
|||||
|
9 |
8 |
7 |
6 |
5 |
9 |
8 |
|
+ P A |
+ P A |
P A |
= 2 /14+ 2 /14+ 4 /14+ 0 3 /14 = |
|||||
7 |
6 |
|
5 |
|
|
|
|
|
11/14 |
|
|
|
|
|
|
|
|
Пример 3. Вероятность того, что отдельно взятая таблетка с конвейера будет бракованной равна 0.01. Найти вероятность того, что из 3-х случайно выбранных с конвейера таблеток бракованными будут: а) одна, б) три, в) ни одной.
Решение:
Введем следующие обозначения:
A1 ={«1-я таблетка является бракованной»}, |
|
A1 |
={«1-я таблетка не является бракованной»}, |
A2 |
={«2-я таблетка является бракованной»}, |
A2 |
={«2-я таблетка не является бракованной»}, |
A3 |
={«3-я таблетка является бракованной»}, |
A3 |
={«3-я таблетка не является бракованной»}. |
а) Введём обозначение: |
|
A ={«Одна таблетка из 3 является бракованной»}, |
|
Заметим, что в условии задачи не указывается, какая по счёту таблетка является брако- |
|
ванной, поэтому бракованной может быть или первая, или вторая, или третья таблетка. Но в условии говорится о том, что одновременно две оставшихся таблетки должны быть не бракованными. Поэтому событие A будет состоять в следующем: бракованной является первая таблетка, но тогда одновременно с этим вторая и третья таблетки будут не бракованными, либо бракованной является вторая таблетка, но тогда одновременно с этим первая и третья таблетки будут не бракованными, либо, наконец, бракованной будет третья таблетка, но тогда одновременно с этим не бракованными будут первая и вторая таблетки. Три перечисленных случая будут несовместными, и при этом может реализоваться только один из них (сложение несовместных случаев – логическое «И»); кроме этого в каждом из перечисленных случаев совместно (одновременно) происходят три события (произведение совместных событий – логическое «И»). Поэтому событие A можно записать в виде:
A= A1 A2 A3 + A1 A2 A3 + A1 A2 A3 .
Используем теоремы сложения и умножения для нахождения искомой вероятности: |
||||||||||||||||||
P A = P A A A + A A A + A A A |
= P A A A |
|
|
|||||||||||||||
|
|
1 |
2 |
3 |
|
1 |
2 |
3 |
1 |
2 |
3 |
|
1 |
2 |
3 |
|
|
|
+ P A A A + P A A A = P A P A |
P A + |
|
|
|
|
|||||||||||||
1 |
2 |
3 |
P A |
1 |
2 |
3 |
P A |
1 |
|
|
2 |
3 |
|
|
|
|
||
P A |
P A |
+ P A |
P A |
0.01 0.99 0.99 |
|
|||||||||||||
1 |
|
2 |
|
3 |
|
|
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
+ 0.99 0.01 0.99 + 0.99 0.99 0.01= 0.029 = 2.9% |
|
|
||||||||||||||||
б) Введём следующее обозначение: |
|
|
|
|
|
|
||||||||||||
A ={«3 таблетки являются бракованными»}. |
|
|
|
|||||||||||||||
Представим событие |
A |
в виде комбинации событий A1 , A2 , A3 . Событие |
A произой- |
|||||||||||||||
дет в том случае, если одновременно (совместно) все три таблетки будут бракованными, т. е. A= A1 A2 A3 . Используем теорему умножения вероятностей совместных событий и находим искомую вероятность:
P A = P A1 A2 A3 = P A1 P A2 P A3 =
0.01 0.01 0.01= 10 6 = 10 4%
11

в) Введём следующее обозначение: |
|
|
|
|
|
|
|
|
A ={«ни одна из таблеток не является бракованной»}. |
|
|
|
|
|
|
|
|
Представляем событие A в виде комбинации событий |
A1 |
, |
A2 |
, |
A3 |
. Событие |
A |
про- |
изойдет в том случае, когда одновременно (совместно) все три таблетки не будут бракован-
ными, т. е. |
A A1 A2 |
A3 |
. Используем теорему умножения вероятностей совместных событий |
||||
и получаем: |
|
|
|
= P A |
P A |
P A = 0.99 0.99 0.99 = 0.97 |
|
P A = P A A A |
|||||||
|
1 |
2 |
3 |
|
1 |
2 |
3 |
Пример 4. Слово «МИР» написали на карточке, которую потом разрезали на буквы, а буквы поместили в непрозрачный ящик. Найти вероятность того, что при последовательном извлечении букв из ящика получится слово «РИМ». Решить задачу с учётом того, что буквы в ящик а) не возвращаются, б) возвращаются.
Решение:
а) Если карточки назад не возвращаются, то вероятность извлечения той или иной буквы будет зависеть от того, какие буквы были извлечены на предыдущих этапах. Таким образом, мы имеем дело с условной вероятностью. Вводим следующие обозначения:
AР={«Была извлечена буква Р»},
AИ={«Была извлечена буква И»},
AМ={«Была извлечена буква М»}.
Вероятности этих событий будут зависеть от того, в каком порядке извлекаются кар-
точки. |
|
|
|
|
|
|
|
|
Вводим ещё одно обозначение: |
|
|
|
|
||||
A={«Из извлеченных букв было составлено слово РИМ»}, |
|
|
|
|
||||
Представим событие |
A в виде комбинации событий AР , |
AИ , |
AМ |
. Событие A реали- |
||||
зуется в том случае, если вначале будет извлечена буква «Р» (событие |
AР ), затем буква – |
|||||||
«И» (событие |
AИ ), при условии, что перед этим была извлечена буква «Р», и, потом, нако- |
|||||||
нец, – буква «М» (событие |
AМ ), при условии, что перед этим была извлечена буква «И»: |
|||||||
A= A A |
/ A |
A |
/ A . Находим вероятности событий |
A |
, A |
, A |
: |
|
Р |
И |
Р |
М |
И |
Р |
И |
М |
|
P A |
= |
Р |
|
1 3
,
P AИ
/ A |
= |
Р |
|
1 2
,
P AМ
/
AИ
=
1
.
Используем теорему умножения вероятностей зависимых событий и получим искомую вероятность:
P A = P A |
P A |
/ A |
P A |
Р |
И |
Р |
М |
/ A |
= |
1 |
|
1 |
1= |
|
|
||||
И |
|
3 |
|
2 |
|
|
|
|
|
1 6
.
б) Если карточки назад возвращаются, то вероятность извлечения той или иной буквы не зависит от того, какие буквы были извлечены на предыдущих этапах. Таким образом, все буквы будут иметь одинаковую вероятность извлечения. Используем те же обозначения, что и в предыдущем пункте, и опишем событие A . Событие A реализуется в том случае, если вначале будет извлечена буква «Р» (событие AР ), затем буква – «И» (событие AИ ), и по-
том – буква «М» (событие AМ ), т. е. эти события произойдут совместно: A= AР AИ AМ . Находим вероятности событий AР , AИ , AМ :
12

P AР = |
1 |
, P AИ = |
1 |
, P AМ = |
1 |
. |
|
3 |
3 |
3 |
|||||
|
|
|
|
Используем теорему умножения вероятностей совместных событий и получим искомую вероятность:
P A = P A |
P A |
P A |
|
1 |
|
1 |
|
1 |
|
1 |
. |
|
|
|
|
||||||||
Р |
И |
М |
|
3 |
|
3 |
|
3 |
|
27 |
|
|
|
|
|
|
|
|
|
1.2. Повторные независимые испытания
1.2.1. Повторные независимые испытания. Формула Бернулли
Говорят, что задача подчиняется схеме Бернулли, если при повторных независимых испытаниях выполняются следующие условия:
1.число испытаний n конечно;
2.каждое испытание имеет только два исхода: первый – событие А осуществилось, и второй – событие А не осуществилось;
3.все испытания независимые;
4.вероятность появления события А в каждом испытании постоянна.
Если при выполнении n независимых повторных испытаний вероятность осуществления события А в каждом отдельном испытании равна p (вероятность противоположного события равна q=1–p), то вероятность осуществления события А ровно m раз в n испытаниях выражается формулой Бернулли:
p |
(m) C |
m |
p |
m |
q |
n m |
|
n! |
p |
m |
q |
n m |
|
||||||||||||
n |
|
|
|
|
|
|||||||
n |
|
|
|
|
|
|
m!(n m)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При большом нительно, т. к. это формулами.
числе n повторных испытаний пользоваться формулой Бернулли затрудсвязано с большими числами, поэтому используются её предельными
1.2.2. Локальная теорема Муавра – Лапласа.
Если вероятность осуществления некоторого события А в n испытаниях постоянна и отлична от 0 и 1, то вероятность pn(m) того, что в n независимых испытаниях событие А осуществится ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции:
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
||
y |
|
e |
2 |
|
|
|
(x) |
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
npq |
|
2 |
|
|
|
|
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
m np |
|
||
|
|
|
1 |
|
|
|
|
|
|
|||||
где: (x) |
|
e |
|
|
, |
x |
. |
|||||||
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
npq |
|
|
Функция |
(x) |
четная, т.е. ( x) (x) . Значения функции |
||||||||||||
цах (см. таблицу 1).
(x)
можно найти в табли-
1.2.3. Формула Пуассона
Если n велико, но при этом вероятность p события мала (p≤0.1). В этом случае пользуются асимптотической формулой Пуассона (законом редких событий):
pn (m) m e m!
где: np . Приближенное правило применения формулы Пуассона состоит в том, что n должно быть не меньше нескольких десятков, а лучше сотен, значение параметра μ должно
13

находиться между 0 и 10. При больших μ рекомендуется применять теорему Муавра – Лапласа.
Примеры решения задач
Пример 5. Вероятность выигрыша одного лотерейного билета равна 0.25. Найти вероятность того, что 4-х билетов выигрышным окажется а) один, б) хотя бы один.
Решение:
а) Заметим, что данную задачу можно решить, используя теоремы сложения и умножения, однако технически быстрее решить данную задачу с помощью формулы Бернулли. Предварительно убедимся в том, что условие задачи удовлетворяет схеме Бернулли:
1. Число испытаний конечно – в нашем случае это число равно количеству лотерейных билетов ( n = 4 ).
2. В единичном испытании возможны только 2 исхода: либо событие A происходит, либо не происходит. В нашем случае либо один билет выигрывает, либо – нет.
3. В каждом единичном испытании вероятность события A остаётся постоянной. В нашем случае каждый билет имеет одинаковую вероятность выигрыша равную p = 0.25 .
4. События в каждом испытании являются независимыми. В нашем случае выигрыш или проигрыш отдельного билета не зависит от того, как сыграли другие билеты.
Так как все требования выполняются, то данная задача удовлетворяет схеме Бернулли. Будем использовать формулу Бернулли:
P m = |
n! |
|
m! n m ! |
||
n |
||
|
p |
n |
q |
n m |
|
|
.
В нашем случае
n =
4
,
m
=
1
,
p =
0.25
,
q = 1
p = 1 0.25=
0.75
. Подставляя числа, получаем искомую вероятность:
P 1 = |
4! |
1 |
4 1 |
= |
1 2 3 4 |
3 |
|
0.25 0.75 |
|
|
0.25 0.75 |
||
4 |
1!(4 -1)! |
|
|
|
1 1 2 3 |
|
|
|
|
|
|
=
0.42
.
б) Выражение «выиграет хотя бы один билет» означает, что из 4 билетов выиграют или
1, или 2, или 3 или 4 билета одновременно. |
|
|
|
||||||||||
Вводим следующие обозначения: |
|
|
|
|
|
||||||||
A1={«Выиграл 1 билет из 4»}, |
|
|
|
|
|
|
|||||||
A2={«Выиграли 2 билета из 4»}, |
|
|
|
|
|
||||||||
A3={«Выиграли 3 билета из 4»}, |
|
|
|
|
|
||||||||
A4={«Выиграл 4 билета из 4»}, |
|
|
|
|
|
||||||||
A={«Выиграл хотя бы один билет из 4»}. |
|
|
|
||||||||||
Представляем событие |
A в виде комбинации несовместных (так как произойдёт только |
||||||||||||
одно из них) событий |
A |
, A |
, A , |
A : A = A + A + A + A . |
|||||||||
|
|
|
|
1 |
2 |
|
3 |
4 |
|
1 |
2 |
3 |
4 |
Используем теорему сложения несовместных событий, чтобы найти искомую вероят- |
|||||||||||||
ность: |
|
|
|
|
|
|
|
|
|
|
|
|
|
P A = P A1 + A2 + A3 + A4 = P A1 |
+ P A2 |
+ P A3 + P A4 . |
|||||||||||
Находим сейчас вероятности |
P A |
, |
P A |
, P A |
, |
P A с помощью формулы Бернул- |
|||||||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
4 |
|
ли: |
|
|
|
|
|
|
|
|
|
|
|
|
|
P A |
= P 1 = |
|
|
4! |
|
0.2510.754 1 |
= |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
1 |
4 |
1!(4 |
1)! |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
1 2 3 4 0.25 0.753 = 0.42, 1 1 2 3
14

P A |
= P 2 = |
4! |
0.25 |
2 |
0.75 |
4 2 |
= |
|
|
|
|||||||
|
|
|
|
|||||
2 |
4 |
2!(4 |
2)! |
|
|
|
|
|
|
|
|
|
|
|
|
||
1 2 3 4 0.252 0.752 = 0.21, 1 2 1 2
P A |
= P 3 = |
4! |
|
0.2530.754 3 = |
|
|
|||
3 |
4 |
3!(4 3)! |
|
|
|
|
|
||
1 2 3 4 0.253 0.75 = 0.05, 1 2 3 1
P A |
= P 4 = |
|
4! |
0.25 |
4 |
0.75 |
4 4 |
= |
|||||
|
|
|
|||||||||||
|
|
|
|
|
|||||||||
|
4 |
|
4 |
4!(4 |
4)! |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
1 2 3 4 |
0.25 |
4 |
|
0.75 |
0 |
= 0.004. |
|
|
||||
|
|
|
|
|
|||||||||
1 2 3 |
4 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Складывая, получаем искомую вероятность: |
||||
P A = P A |
+ P A |
+ P A |
+ P A |
= |
1 |
2 |
3 |
4 |
|
0.42+ 0.21+ 0.05+ 0.004 = 0.684. |
|
|||
б*) Отметим, что есть более короткий способ решения данной задачи. Событие «выиграет хотя бы один билет» является противоположным событию «не выиграл ни один билет».
Вводим обозначение: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
A0={«Не выиграл ни один билет»} |
|
|
|
||||||||||||
Так как события являются противоположными, то событие |
A можно выразить через |
||||||||||||||
событие |
A0 |
следующим образом: |
A = A0 . Тогда их вероятности будут связаны выражени- |
||||||||||||
ем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P A =1 P A =1 P A0 . |
|
|
|
|
|
||||||||||
Находим вероятность события |
A0 |
по формуле Бернулли: |
|
||||||||||||
P A |
= P 0 = |
|
|
4! |
|
0.25 |
0 |
0.75 |
4 0 |
= |
|
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||
|
0 |
4 |
|
0!(4 |
0)! |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
1 2 3 4 |
0.25 |
0 |
0.75 |
4 |
= 0.316. |
|
|
|
||||||
|
|
|
|
|
|||||||||||
|
2 3 4 |
|
|
|
|
|
|||||||||
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Окончательно находим искомую вероятность: |
|
||||||||||||||
P A = 1 P A = 1 P A0 |
= 1 0.316 = 0.684. |
|
|||||||||||||
Пример 6. Вероятность того, что в течение дня в аптеке будет куплена упаковка неко- |
|||||||||||||||
торого препарата равна |
|
p = 0.46 . Найти вероятность того, что в течение дня из 100 упако- |
|||||||||||||
вок будет куплено 50. |
|
|
|
|
|
|
|
|
|
|
|||||
Решение:
Убедимся, что условие задачи позволяет использовать схему Бернулли:
1. |
Число испытаний конечно – в нашем случае это число равно количеству упаковок |
препарата ( n =100 ). |
|
2. |
В единичном испытании возможны только 2 исхода: либо событие A происходит, |
либо – не происходит. В нашем случае упаковку приобретают, либо – нет. |
|
3. |
В каждом единичном испытании вероятность события A остаётся постоянной. В |
нашем случае для каждой упаковки вероятность приобретения остаётся постоянной и равной p = 0.46 .
4. События в каждом испытании являются независимыми. В нашем случае покупка одной упаковки никак не влияет на вероятность покупки других.
15
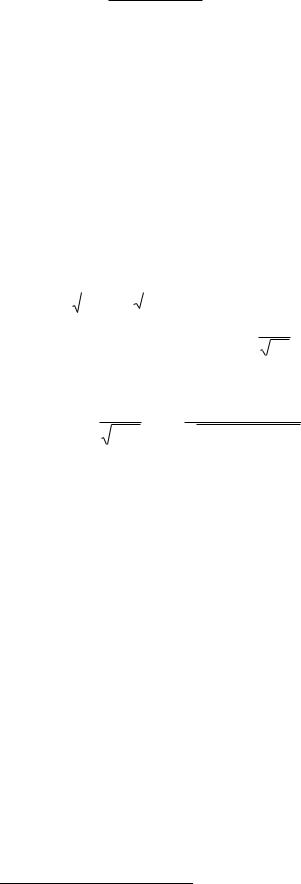
Так как все условия соблюдены, то можно использовать формулу Бернулли. Однако при попытке её использовать возникают проблемы вычислительного характера:
P |
50 = |
100 |
|
100! |
0.46 |
50 |
100 50 |
50!(100 50)! |
|
0.54 |
|
|
|
|
. Вычислить такие факториалы и степени до-
вольно трудно, поэтому будем использовать один из предельных случаев теоремы Бернулли: либо локальную теорему Муавра – Лапласа, либо формулу Пуассона. В литературе встречаются различные рекомендации по способам выбора той или иной формулы. Будем использовать следующие правила выбора формул:
Для локальной теоремы Муавра – Лапласа: |
npq >10 , |
|
|
|
|||
Для формулы Пуассона: |
|
|
|
|
|
|
|
1. |
np 10 , |
|
|
|
|
|
|
2. |
p 0.1. |
|
|
|
|
|
|
В |
нашей задаче: n =100 |
, |
m = 50 , |
p = 0.46 |
, |
q = 1 p = 1 0.46 = 0.54 |
; |
npq = 100 0.46 0.54 25 >10 , поэтому будем использовать локальную теорему Муавра –
Лапласа. |
|
Предварительно вычисляем вспомогательную величину |
x : |
x = |
m np |
= |
50 100 0.46 |
|
= 0.80 . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
npq |
100 0.46 0.54 |
|
|
|
|
||||||||
По таблице 1 для функции |
1 |
e |
x |
2 |
/ 2 |
находим соответствующее значение функ- |
||||||||
|
||||||||||||||
2π |
|
|
|
|||||||||||
ции *: 0.80 |
|
|
|
|
|
|
|
|
|
|
||||
= 0.2897 . |
|
|
|
|
|
|
|
|
||||||
Наконец, по локальной теореме Муавра – Лапласа находим искомую вероятность:
P m |
1 |
|
|
n |
npq |
|
x =
1 
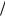 100 0.46 0.54
100 0.46 0.54
0.2897 =
0.058
.
Пример 7. Вероятность |
заболевания некоторым редким заболеванием в некоторой |
местности равна p = 0.001 |
. Найти вероятность того, что из 10000 жителей больными ока- |
жутся а) двое, б) хотя бы 1.
Решение:
а) Убедимся, что условие задачи соответствует схеме Бернулли:
1. |
Число испытаний конечно – в нашем случае это число |
равно количеству жите- |
лей( n =1000 ). |
|
|
2. |
В единичном испытании возможны только 2 исхода: либо событие A происходит, |
|
либо – не происходит. В нашем случае житель либо болен, либо – нет. |
||
3. |
В каждом единичном испытании вероятность события A |
остаётся постоянной. В |
нашем случае для каждого жителя по условию задачи вероятность заражения остаётся по-
стоянной и равной |
p = 0.001. |
4. События в каждом испытании являются независимыми. В нашем случае по условию задачи вероятность заражения для каждого жителя не зависит от того, заражены ли остальные.
Так как все условия соблюдены, то можно использовать формулу Бернулли. Однако при попытке её использовать возникают проблемы вычислительного характера:
P |
2 = |
1000! |
|
0.00120.9991000 2 . |
|
|
|||
1000 |
2!(1000 2)! |
|
||
|
|
|
||
* Отметим, что функция φ(x) является чётной, т. е. φ(–x)= φ(x). Например, φ(–0.8)= φ(0.8)
16

Вычислить такие факториалы и степени довольно трудно, поэтому будем использовать один из предельных случаев теоремы Бернулли: либо формулу Муавра – Лапласа, либо формулу Пуассона. Так как np = 1000 0.001= 1 и p = 0.001< 0.1, то будем использовать фор-
мулу Пуассона. Предварительно вычислим параметр
λ =
np
,
λ
=
1000
0.001=
1
. Использу-
ем сейчас формулу Пуассона:
Pn m λm e λ . Подставляя числа m = 2 , λ = 1 , получаем искомую вероятность: m!
P |
2 |
1000 |
|
2 |
|
|
|
1 |
e |
1 |
= |
|
|||
2! |
|
||
|
|
|
0.184
.
б) Условие «хотя бы 1 житель окажется болен» обозначает, что больными окажутся 1 житель, 2 жителя, 3 жителя и т. д. до 1000. Находить вероятности всех указанных событий затруднительно, поэтому будем использовать решение с помощью противоположного события. Событием противоположным событию «хотя бы 1 житель окажется болен» является событие «ни один житель не является больным». Вводим обозначения:
A0={«Ни один житель не является больным»}, A≥1={«Хотя бы один житель является больным»}.
Так как эти события являются противоположными, то их вероятности связаны формулой: P A 1 =1 P A0 . Для нахождения вероятности P A0 используем формулу Пуассона:
P |
0 |
10 |
|
e 1 = 0.368 . |
|
|
|||||
1000 |
|
0! |
|
||
|
|
P A 1 =1 P A0 |
|||
По формуле |
|||||
P A |
|
= 1 P A = 1 0.368 = |
|||
1 |
|
|
|
0 |
|
находим искомую вероятность:
0.632 .
17
ГЛАВА 2. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
2.1. Случайные величины: дискретные и непрерывные
Количественная характеристика испытания состоит в определении значений некоторых величин, которые находят (измеряют) при данном испытании. В силу действия большого числа неконтролируемых факторов эти величины могут принимать различные значения в результате испытания, причем до испытания невозможно предсказать значение этих величин. Изучение таких величин в теории вероятностей требует связать их с полем событий данного испытания. (Поле событий – совокупность всех случайных событий данного испытания, для которых определены вероятности.)
Случайная величина (СВ) – такая величина, которая в результате испытания примет одно и только одно возможное значение, но заранее неизвестно, какое именно. (Обозначаются случайные величины буквами X, Y, Z,…, а их возможные значения – x, y, z,…,соответственно.)
Дискретной называют случайную величину, принимающую любое из ряда отдельных друг от друга возможных значений с определенными вероятностями. Число возможных значений может быть конечно или бесконечно. (Пример: количество студентов на лекции.)
Непрерывной называют случайную величину, которая может принимать любое значение из интервала (конечного или бесконечного). Число возможных значений непрерывной случайной величины бесконечно. (Пример: продолжительность человеческой жизни, размеры любых физических объектов, давление, температура.)
Задание вероятностей принятия случайной величиной своих значений в той или иной форме называется заданием распределения случайной величины.
2.2. Закон распределения дискретной случайной величины
Для дискретной случайной величины законом ее распределения называется соответствие между ее возможными значениями и их вероятностями. Такое соответствие можно задать с помощью таблицы (ряда распределения):
X |
x1 |
x2 |
… |
xn |
p |
p1 |
p2 |
… |
pn |
или графика (многоугольника распределения):
18
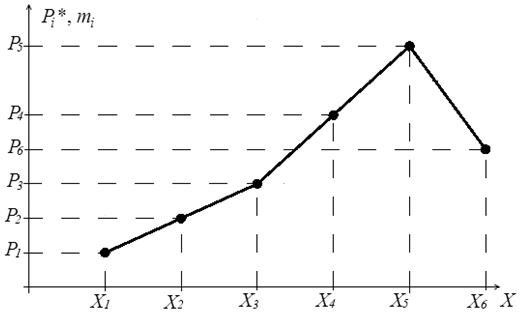
При этом сумма всех вероятностей pi должна быть равна 1 (условие нормировки):
n |
P P |
... P 1 |
|
P |
|||
i |
1 |
2 |
n |
i 1 |
|
|
|
2.3. Функция распределения дискретной случайной величины.
Рассмотрим вероятность того, что случайная величина X окажется меньше некоторого заданного числа x:
P(X x) F(x)
Эта вероятность называется функцией распределения вероятностей случайной ве-
личины X (или интегральной функцией распределения).
Функция распределения вероятностей случайной величины X вполне определяет эту случайную величину. Она может быть использована для записи распределений как непрерывных (на графике будет плавной кривой), так и дискретных случайных величин (на графике будет ступенчатой линией).
Свойства функции распределения:
1. |
0 F(x) 1 |
; |
|
2.F(x) – неубывающая функция
3.Вероятность попадания случайной величины X в интервал
[ ; ]
равна разности
между значениями функции распределения в правом и левом концах интервала:
P( x ) F( ) F( ) |
|
|
|
|
2.4. Математические |
характеристики |
дискретных |
случайных |
вели- |
чин: математическое ожидание, дисперсия, среднее квадратическое отклонение
Характеристики положения:
1. Математическое ожидание является центром распределения, обозначается М(X) или μ и вычисляется по формуле:
n |
x P x P |
... x P . |
M ( X ) x P |
||
i i |
1 1 2 2 |
n n |
i 1 |
|
|
|
|
19 |

2.Модой Мо(X) называют такое значение случайной величины X, для которого соседние значения величины X имеют вероятности, меньше, чем для данного. Распределения СВ могут быть одно-, двух-, а также многомодальными.
3.Медианой Ме(X) называют такое значение X, которое делит все распределение на две равновероятные части:
P(X Me) P(X
Me)
1/
2
.
Если распределение СВ одномодальное и симметрично, то М(X), Мо(X), Ме(X) совпадают.
Характеристики рассеяния:
1. Дисперсия D(X) или σ2 – математическое ожидание квадрата отклонения случайной величины X от ее математического ожидания:
2 |
n |
|
2 |
|
|
) (x |
) |
P |
|||
D( X ) M (( X ) |
|
||||
|
i |
|
|
i |
|
|
i 1 |
|
|
|
Дисперсия характеризует меру разброса значений случайной величины относительно ее центра распределения (математического ожидания). D(X) имеет размерность квадрата случайной величины.
2. Среднее квадратическое отклонение σ:

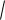 D( X )
D( X )
Среднее квадратическое отклонение также характеризует рассеяние случайной величины, размерность величины σ совпадает с размерностью величины X.
Примеры решения задач Пример 8. Дискретная случайная величина задана следующим законом распределения:
x |
|
|
0 |
|
|
2 |
|
3 |
|
|
5 |
P |
|
|
P |
|
0.2 |
|
0.3 |
|
|
0.1 |
|
|
|
1 |
|
|
|
|
|||||
Найти: а) неизвестную |
вероятность P1 , |
б) математическое ожидание, |
в) дисперсию, |
||||||||
г) среднее квадратическое отклонение; д) построить многоугольник распределения. |
|||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
а) Для нахождения неизвестной вероятности P1 |
используем свойство закона распреде- |
||||||||||
ления дискретной случайной величины: Pi = 1. Таким образом, получаем уравнение: |
|||||||||||
P |
|
|
|
|
|
|
|
|
P |
|
|
1 +0.2+0.3+0.1= 1. Откуда получаем искомую вероятность |
1 = 0.4 . |
|
|||||||||
б) Для нахождения математического ожидания используем формулу: |
|
||||||||||
M x = xi Pi . |
|
|
|
|
|
|
|
|
|
||
Подставляя числа из условия задачи, получаем искомую величину: |
|
||||||||||
M x = x P = 0 0.4+ 2 0.2+3 0.3+5 0.1= 1.8. |
|
|
|
||||||||
|
i i |
|
|
|
|
|
|
|
|
|
|
в) Для нахождения дисперсии используем формулы: |
|
|
|
||||||||
D(x) x M x 2 P |
или D(x) x 2 P M x 2 . |
|
|
|
|||||||
|
i |
i |
|
i |
i |
|
|
|
|
|
|
Вторую формулу рекомендуем использовать при вычислениях «вручную» (без помощи |
|||||||||||
ЭВМ) в том случае, если разность xi M x |
не является целым числом. |
|
|||||||||
Подставляя числа из условия задачи, получаем искомую величину: |
|
||||||||||
D(x) xi |
2 Pi M x 2 |
02 0.4 22 0.2 32 0.3 |
|
|
|
|
|
||||
52 0.1 1.82 2.76.
г) Среднее квадратическое отклонение найдем по формуле:
20
