38

1. Механические колебания: гармаонические, затухающие.

Свободными колебаниями называют такие, торые совершаются без внешних воздействий за счет первона­чально полученной телом энергии.Характерными моделями та­ких механических колебаний являются пружинный маятник математический маятник.

Гармонические колебания: х = Acos (ω₀t+ф₀), где w₀t + ф₀ = ф — фаза колебаний, ф₀ — начальная фаза (при t = 0), ω₀ — круговая частота колебаний, А — их амплитуда.

Амплитуда и начальная фаза колебаний определяются началь­ными условиями движения, т. е. положением и скоростью мате­риальной точки в момент t = 0.

Таким образом, материальная точка, подвешенная на пружине (пружинный маятник) или нити (математический маятник), со­вершает гармонические колебания, если не учитывать силы со­противления.

Затухающие колебания.В реальном случае на колеблющее­ся тело действуют силы сопротивления (трения), характер движе­ния изменяется, и колебание становится затухающим:

x= A0e^-βtcos(ωt+φ0), где β — коэффициент затухания;ω₀ — круговая частота соб­ственных колебаний системы (без затухания).

2. Энергия гармонических колебаний

Кинетическую энергию материальной точки, колеблющейся по гармоническому закону, можно вычислить используя выражение:

Е_к =1/2mv²_msin²(ω₀t +φ₀)= 1/2

mA²ω²osin²(_ωot+ф₀) =

=1/2kA²sin² (ω₀t+_Фо).

Потенциальную энергию колебательного движения найдем, исходя из общей формулы для потенциальной энергии упругой

деформации Е_п=1/2kx²:Е_П=1/2kA²cos²(ωоt+_Фо).

Складывая кинетическую и потенциальную энер­гии, получаем полную механическую энергию материальной точки, колеблющейся по гармоническому закону: E=E_К+E_П=1/2kA² sin²(ωоt+_Фо)+1/2кА² cos² (ωоt+_Фо)=1/2kA²[sin²(ωоу+ф₀) +cos²(ωоt+_Фо)]=1/2kA².

3. Вынужденные колебания. Резонанс. Автоколебания.

Вынужденными колебаниями называются колебания, возни­кающие в системе при участии внешней силы, изменяющейся по периодическому закону. Частота вынуж­денного колебания равна частоте вынуждающей силы: х=Acos(ωоt+ф₀).

Амплитуда вынужденного колебания прямо пропорци­ональна амплитуде вынуждающей силы и имеет сложную зави­симость от коэффициента затухания среды и круговых частот соб­ственного и вынужденного колебаний. Если ω₀ и β для системы заданы, то амплитуда вынужденных колебаний имеет максималь­ное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Само явление — достижение максимальной амплитуды вынужденных колебаний для за­данных ω₀ и β— называют резонансом. Вредное действие резонанса связано главным об­разом с разрушением, которое он может вызвать. Так, в технике, учитывая разные вибрации, необходимо предусматривать воз­можное возникновение резонансных условий, в противном случае могут быть разрушения и катастрофы.

Незатухающие колебания, существующие в какой-либо сис­теме с затуханием при отсутствии переменного внешнего воз­действия, называются автоколебаниями, а сами системы — автоколебательными. Классическим примером механической автоколебательной сис­темы являются часы, в которых маятник или баланс являются ко­лебательной системой, пружина или поднятая гиря — источником энергии, а анкер — регулятором поступления энергии от источни­ка в колебательную систему.

Многие биологические системы (сердце, легкие и др.) являют­ся автоколебательными. Характерный пример электромагнитной автоколебательной системы — генераторы электромагнитных ко­лебаний.

4. Сложение колебаний, направленных вдоль одной прямой и во взаимно перпендикулярных направлениях.

Рассмотрим сложение одинаково направленных колебаний одного периода, но отличающихся начальной фазой и амплитудой. Уравнения складываемых колебаний заданы в следующем виде:

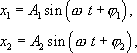
где и- смещения;и- амплитуды;и- начальные фазы складываемых колебаний. Амплитуду результирующего колебания удобно определить с помощью векторной диаграммы (рис. 7.5), на которой отложены векторы амплитудA1и A2складываемых колебаний под углами ик оси х и по правилу параллелограмма получен вектор амплитуды суммарного колебанияA. Если равномерно вращать систему векторов (параллелограмм) и проектировать векторы на ось OY, то их проекции будут совершать гармонические колебания в соответствии с заданными уравнениями. Взаимное расположение векторов A1, и A2 при этом остается неизменным, поэтому колебательное движение проекции результирующего вектора Aтоже будет гармоническим.

Отсюда следует вывод, что суммарное движение - гармоническое колебание, имеющее заданную циклическую частоту. Определим модуль амплитуды А результирующего колебания В угол(из равенства противоположных углов параллелограмма).

Следовательно отсюда

. Согласно теореме косинусов

Начальная фаза результирующего колебания определяется из:

Соотношения для фазы и амплитуды позволяют найти амплитуду и начальную фазу результирующего движения и составить его уравнение

Биения

Рассмотрим случай, когда частоты двух складываемых колебаний мало отличаются друг от друга , и пусть амплитуды одинаковы и начальные фазы, т.е.Сложим эти уравнения аналитически

ПреобразуемТогда

Так как все же медленно изменяется, величинунельзя назвать амплитудой в полном смысле этого слова (амплитуда величина постоянная). Условно эту величину можно назвать переменной амплитудой. График таких колебаний показан на рис. 1.6 Складываемые колебания имеют одинаковые амплитуды, но различны периоды, при этом периодыотличаются незначительно друг от друга. При сложении таких колебаний наблюдаются биения. Число n биений в секунду определяется разностью частот складываемых колебаний, т.е.Биения можно наблюдать при звучании двух камертонов, если частоты и колебаний близки друг к другу.

Сложение взаимно перпендикулярных колебаний.

Пусть материальная точка одновременно участвует в двух гармонических колебаниях, совершающихся с одинаковыми периодами Т в двух взаимно перпендикулярных направлениях. С этими направлениями можно связать прямоугольную систему координат XOY, расположив начало координат в положении равновесия точки. Обозначим смещение точки С вдоль осей ОХ и OY, соответственно, через х и у.

Начальная разность фаз равна π Уравнения колебания в этом случае имеют вид:

Следовательно, точка С колеблется вдоль отрезка прямой, проходящей через начало координат, но лежащие в других квадрантах, чем в первом случае. Амплитуда А результирующих колебаний в обоих рассмотренных случаях равна

В. Начальная разность фаз равна .

Уравнения колебаний имеют вид: Разделим первое уравнение на, второе - на:

При равных

амплитудах траекторией суммарного движения будет окружностьВ общем случае при, но кратным, т.е., при сложении, взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу. Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.