
- •КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
- •Комплексные числа
- •Действия над комплексными числами
- •Тригонометрическая и показательная формы комплексного числа
- •ПОНЯТИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- •Плоскость комплексного переменного
- •Стереографическая проекция
- •Последовательности комплексных чисел и пределы последовательностей
- •Понятие функции комплексного переменного
- •Предел и непрерывность функции комплексного переменного
- •ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- •Связь между аналитическими и гармоническими функциями
- •Геометрический смысл производной функции комплексного переменного. Понятие конформного отображения
- •КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
- •Линейная функция
- •Дробно-линейная функция
- •Степенная функция. Понятие римановой поверхности
- •Показательная функция
- •Логарифмическая функция
- •Общая степенная функция
- •Функция Жуковского
- •Тригонометрические функции
- •Общие свойства конформных отображений
- •ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
- •Интеграл от функции комплексного переменного
- •Интегральная теорема Коши
- •Интегральная формула Коши и ее следствия
3.3.Геометрический смысл производной функции комплексного переменного. Понятие конформного отображения
Напомним вначале некоторые сведения о кривых. Как было отмечено в § 2 п.1, каждая кривая на плоскости может быть задана параметрическими уравнениями
x = x(t); y = y(t); при 6 t 6 ; |
(3.8) |
где x(t), y(t) действительные функции действительного переменного t.
Если функции x(t), y(t) имеют непрерывные производные на интервале ( ; ), причем x0(t) и y0(t) одновременно не обращаются в нуль, то кривая называется гладкой.
Так как каждая точка (x; y) на плоскости задается комплексным числом z = x+iy, то уравнения (3.8) можно записать в более компактной форме:
z(t) = x(t) + iy(t); 6 t 6 :
Возьмем значение t0 2 ( ; ). Ему соответствует точка (x0; y0), где x0 = x(t0), y0 = y(t0). Известно, что вектор (x0(t0); y0(t0)) направлен по касательной к кривой в точке (x0; y0). Значит, и соответствующее комплексное число
z0(t0) = x0(t0) + iy0(t0)
изображается этим касательным вектором. Удобно изображать этот вектор исходящим не из начала координат, а из точки
(x0; y0).
Пусть теперь задана функция f(z), аналитическая в точке z0, причем f0(z0) 6= 0. Предположим далее, что через точку z0 проходит кривая , заданная уравнением z(t) = x(t) + iy(t) и z(t0) = z0 (см. рис. 3.1).
84
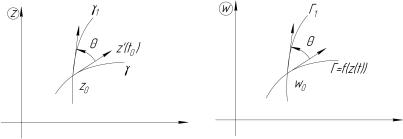
Кривая отображается функцией w = f(z) в кривую , лежащую в плоскости w, уравнение кривой будет иметь вид w = f(z(t)); точка z0 отобразится в точку w0 = f(z0). По правилу дифференцирования сложной функции
w0(t0) = f0(z0) z0(t0): |
(3.9) |
Отсюда следует (см. (1.8)), что |
|
Arg w0(t0) = Arg f0(z0) + Arg z0(t0): |
(3.10) |
Рис. 3.1 |
Рис. 3.2 |
Но z0(t0) есть вектор, касательный к кривой в точке z0 (см. рис. 3.1), a w0(t0) вектор, касательной к кривой в точке w0 (см. рис. 3.2). Поэтому равенство (3.10) позволяет придать величине Arg f0(z0) следующий геометрический смысл: аргумент производной равен углу, на который нужно повернуть касательную в точке z0 к любой кривой, проходящей через эту точку, чтобы получить направление касательной в точке w0 = f(z0) к образу данной кривой при отображении w = f(z). Заметим, что этот угол не зависит от кривой , т.е. касательные ко всем кривым, проходящим через точку z0, поворачиваются при отображении w = f(z) на один и тот же угол. Поэтому если через точку z0 провести какие-либо две кривые и 1 (см.
85
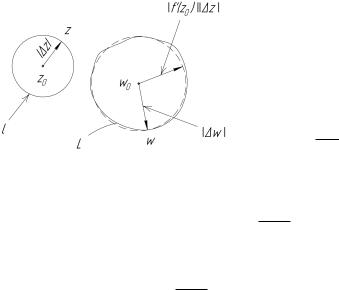
рис. 3.1), то угол между касательными к этим кривым будет равен (как по величине, так и по направлению отсчета) углу между касательными к образам этих кривых. Напомним, что углом между кривыми в точке z0 называется угол между касательными к этим кривым в точке z0. Таким образом, если f0(z0) 6= 0, то отображение w = f(z) сохраняет углы между кривыми. Это свойство называется свойством консерватизма углов.
Выясним далее геометрический смысл модуля производной.
|
|
Зафиксируем |
|
точку |
|||||||
|
z0 и возьмем приращение |
||||||||||
|
аргумента 4z; очевидно, |
||||||||||
|
j4zj |
|
|
равен |
расстоя- |
||||||
|
нию |
|
между |
точками |
|||||||
|
z0 и |
|
z = z0 + 4z |
(рис. |
|||||||
|
3.3). |
Пусть |
w |
= |
f(z), |
||||||
|
4w |
= |
w w0. |
Тогда |
|||||||
|
величина |
4w |
указывает, |
||||||||
|
z |
||||||||||
Рис. 3.3 |
в каком отношении4 |
изме- |
|||||||||
няется расстояние между |
|||||||||||
|
точками в |
|
результате |
||||||||
отображения w = f(z). Предел |
lim |
j4wj |
|
называется коэф- |
|||||||
j4zj |
|||||||||||
|
4z!0 |
|
|
|
|
|
|
||||
фициентом растяжения в точке z0 при отображении w = f(z). Поскольку
lim j4wj = jf0(z0)j;
4z!0 j4zj
то jf0(z0)j равен коэффициенту растяжения в точке z0 при отображении w = f(z). Если jf0(z0)j > 1, то в достаточно малой окрестности точки z0 расстояния между точками при отображении увеличиваются и происходит растяжение; если jf0(z0)j < 1, то отображение приводит к сжатию.
Так как производная f0(z0) не зависит от того, по какому
86

пути точка z = z0+4z приближается к z0, то коэффициент растяжения одинаков во всех направлениях. Это свойство называется свойством постоянства растяжений. Проиллюстрируем его следующим образом. Возьмем окружность ` с центром z0 и радиусом j4zj (см. рис. 3.3). При отображении w = f(z) эта окружность перейдет в кривую L (рис. 3.3); расстояние от точ-
ки w = f(z0 + 4z) этой кривой до точки w0 = f(z0) равно j4wj = jf(z0 + 4z) f(z0)j. Поскольку
4w = f0(z0)4z + (4z) 4z;
где (4z) ! 0 при 4z ! 0, то точки кривой L будут отличаться от окружности с центром w0 и радиусом jf0(z0)jj4zj на величину более высокого порядка малости, чем j4zj.
Отображение называется конформным отображением в точке z0, если: 1) при этом отображении сохраняются углы между любыми двумя кривыми, проходящими через точку z0;
2)растяжение в точке z0 не зависит от направления. Отображение области D на область E называется конформ-
ным отображением области D, если оно непрерывно и конформно в каждой точке области D.
Если конформное отображение сохраняет и направление отсчета углов, то оно называется конформным отображением первого рода; если направление отсчета углов меняется на противоположное, то конформным отображением второго рода.
Пример конформного отображения второго рода дает функция (не аналитическая!) w = z; которая каждую область D отображает на область E, симметричную D, относительно действительной оси.
Полученные выше результаты сформулируем в виде следующей теоремы.
Теорема 3.4. Если функция w = f(z) является аналитической в точке z0 и f0(z0) 6= 0, то f(z) осуществляет
87

конформное отображение первого рода в точке z0. При этом Arg f0(z0) означает угол поворота, a jf0(z0)j коэффициент растяжения при данном отображении.
Если f0(z0) = 0, то отображение, вообще говоря, уже не будет конформным в точке z0. Так, отображение w = z2 увеличивает вдвое углы между лучами в начале координат.
Пример 3.5. Найти угол поворота и коэффициент растя-
жения при отображении w = z i 2 в точке z0 = 2i. z + i
Решение. Вычислим производную
0 |
|
z + i |
|
z + i |
0 |
|
||
w |
= 2 |
z i |
|
|
z i |
|
= 2 |
|
|
|
|
|
|||||
z i |
|
z + i (z i) |
= |
4iz + 4 |
: |
|
z + i |
(z + i)2 |
(z + i)3 |
||||
|
|
Согласно теореме 3.4. коэффициент растяжения при отображении w = f(z) в точке z0 равен модулю значения производной в этой точке, а угол поворота аргументу производной в заданной точке. Вычислим значение производной в точке z0 = 2i:
|
w0(2i) = |
|
4i 2i + 4 |
= |
8 + 4 |
= |
|
4 |
i: |
|||
|
|
(2i + i)3 |
(3i)3 |
27 |
||||||||
|
|
|
|
|
|
|
||||||
Согласно |
(1.1) k |
= |
jw0(2i)j |
= |
4 |
, а |
из |
(1.3) получаем: |
||||
|
|
|||||||||||
27 |
||||||||||||
' = arg(w0 |
(2i)) = |
|
. |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
Задания для аудиторных занятий к § 3
1.Исследовать функцию w = f(z) на дифференцируемость
ианалитичность, в случае аналитичности функции w найти ее производную.
88

1) |
w = iz3 + 2 |
|
2 z: |
5) |
w = |
|
Im z 5iz Re z: |
||||
z |
z |
||||||||||
2) w = (5 3i)z2 4iz + i: |
6) w = (3x2 + 2xy) + i(x3 3x2y): |
||||||||||
3) iz2 + 5 Im z2 2i Re z: |
7) w = z |
2e |
z |
: |
|||||||
|
|
||||||||||
4) |
|
z + 5i |
8) |
w = ez . |
|||||||
w = |
|
: |
|
|
|
|
|
|
|||
iz 7 |
|
|
|
|
|
|
|||||
2. Проверить выполнение условий Коши-Римана для функций z3, ez, cos z, sin z и доказать, что
(z3)0 = 3z2; (ez)0 = ez; (cos z)0 = sin z; (sin z)0 = cos z:
3.Найти области, в которых функция f(z) = jx2 y2j+ +2ijxyj будет аналитической.
4.Доказать, что функция w = ez не дифференцируема во всей комплексной плоскости.
5.Доказать, что функция w = z Re z дифференцируема
только в точке z = 0, найти w0(0). |
|
|
|
|
6. Доказать, что для функции f(z) = |
|
jxyj |
в точке z = 0 |
|
выполняются условия Коши-Римана, но |
производная не суще- |
|||
|
p |
|||
ствует.
7. Найти значения постоянных a; b; c, при которых функция w = f(z) будет аналитической в C.
1)w = x3 + axy2 + 2x + i(bx2y y3 + cy);
2)w = ax2 y2 + b cos x ch y + i(cxy + sin x sh y);
3) w = x2 + |
|
|
ax |
|
+ by2 + i xy + |
|
|
cy |
|
: |
|
|
|
|
|
|
|
|
|||
x |
2 |
+ y |
2 |
x |
2 |
+ y |
2 |
|||
|
|
|
|
|
|
|
8. Найти функции, сопряженные с данными гармоническими функциями в указанных областях.
1) u(x; y) = x2 y2 + x; 0 6 jzj < 1;
x
2) u(x; y) = x2 + y2 ; 0 < jzj < 1;
3) u(x; y) = 12 ln(x2 + y2); 0 < jzj < 1:
9. Существует ли аналитическая функция w = u + iv, для которой:
89

1) |
u(x; y) = |
x2 y2 |
+ x; |
2) |
v(x; y) = ln(x2 + y2) |
|
x2 |
+ y2; |
|
(x2 + y2)2 |
|||||||||
|
|
|
|
|
3)u(x; y) = ey=x:
10.Восстановить аналитическую в окрестности точки z0 функцию w = f(z) по известной действительной части u(x; y)
или мнимой v(x; y) и значению f(z0).
1)v(x; y) = 6y2 6x2 + 3x2y y3; f(3i) = 0;
2)u(x; y) = x2 y2 4y 4 + cos x ch y; f(0) = 3 i;
3)v(x; y) = 2x 2xy + sin x sh y; f(0) = 1;
4)u(x; y) = 1 2y x2 + y2 + sin x ch y; f(0) = 1;
x
5) u = x2 + y2 , f(1) = 1 + i;
6) v(x; y) = (x2 y2) cos x ch y + 2xy sin x sh y; f(0) = i; 7) v(x; y) = 2xy + 4x2 ey sin x; f(0) = 0:
11. Выяснить, существуют ли гармонические функции (отличные от постоянной), и в случае существования найти их.
1) u = '(x); |
|
|
|
|
4) u = '(x2 + y2); |
|
|
||||||||||
3) u = ' y ; |
|
|
|
|
5) u = '(x2 + y): |
|
|||||||||||
2) u = '(xy); |
|
|
|
|
|
u = ' x + x2 |
+ y2 ; |
||||||||||
|
|
|
|
|
|
|
|
|
6) |
|
|
p |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12. Найти коэффициент растяжения k и угол поворота ' |
|||||||||||||||||
для заданного отображения w = f(z) в точке z0. |
|
|
|
|
|||||||||||||
1) w = (z i + 3)2, z0 = 4 5i; |
4) |
w = z cos z, z0 = 1 i; |
|||||||||||||||
2) w = zez, z0 = 1 + p |
3 |
i; |
5) w2= z3 iz2; z0 = p |
3 |
+ i; |
||||||||||||
3) w = |
2z 3i |
; z0 = |
|
3i; |
6) |
|
z 1 |
; z = i: |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
iz + 1 |
|
|
|
|
z + i |
0 |
|
|
|
|
|
|||||
ИДЗ 3
1. Исследовать функцию на дифференцируемость и аналитичность, в случае аналитичности функции w найти ее производную:
1.1. w = sin x sh y i cos x ch y;
90

1.2.w = (3x2 xy) + i(x3 2xy y3);
1.3.w = (x2 + y2) 2i(xy + 2y + 1);
1.4.w = 5z2 (4 + 3i)z + 2i 1;
1.5. w = z2 3i Im z + 2z; |
1.19. w = 2iz Re z2 5z2; |
|||||||||||||||||||||||||
1.6. w = Im z3 2z2 + 3z; |
1.20. w = jzj Im z 3iz2; |
|||||||||||||||||||||||||
1.7. w = 3z2 5iz + 2i; |
|
1.21. w = z Im z 3z2 Re z; |
||||||||||||||||||||||||
1.8. w = (3z + 2)2 5iz 3i; |
1.22. w = (4z 2i)3; |
|
|
|
|
|
|
|||||||||||||||||||
1.9. w = sin x ch y + i cos x sh y; |
1.23. w = ez sin z; |
|
|
|
|
|
|
|||||||||||||||||||
1.10. w = z |
|
z Im z; |
|
1.24. w = 8iz2 4 |
|
+ i; |
||||||||||||||||||||
z |
|
z |
||||||||||||||||||||||||
1.11. w = 2z2 3iz; |
|
|
|
|
1.25. w = |
|
|
Re z + 3iz Im |
|
; |
||||||||||||||||
|
|
|
|
z |
z |
|||||||||||||||||||||
1.12. w = |
|
z2 + Re z2; |
|
1.26. w = |
|
|
Im z + 3z Re z2; |
|||||||||||||||||||
z |
|
z |
||||||||||||||||||||||||
1.13. w = z2 3iz + i Im z; |
1.27. w = 2z3 5iz |
2 + 2i; |
||||||||||||||||||||||||
1.14. w = (z + 1) cos z; |
|
1.28. w = |
3z 2 |
; |
|
|
|
|
|
|
||||||||||||||||
1.15. w = 5z Re z + 2z |
2 |
iz; |
|
|
iz + 1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
|
1.29. w = Im z |
3iz |
+ z; |
|||||||||||||||||||||||
1.16. w = z2 + |
|
+ |
|
|
Re z; |
|
|
|||||||||||||||||||
z |
z |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
Re z; |
1.30. w = ez=z. |
|
|
|
|
|
|
|
|
|
|
|||||
1.17. w = z Im z 3z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1.18.w = (z + 1)e z;
2.Найти значения постоянных a; b; c, при которых функция w = f(z) будет аналитической в C:
2.1.w = x + ay + i(bx + cy);
2.2.w = ax2 + by2 + icxy;
2.3.w = (ch y + a sh y) cos x + i(ch y + b sh y) sin x;
2.4.w = x2 + ax + by2 + i(5y + cxy);
2.5.w = ax2 + by2 x + i(7y + cxy);
2.6. w = |
ax2 + by2 1 |
+ i |
cy |
|
; |
|
(x + 1)2 + y2 |
(x + 1)2 |
+ y2 |
||||
|
|
|
2.7. w = (sin x + a cos x) ch y + i(cos x + b sin x) sh y;
2.8. w = ax2 |
+ bx ay2 + i(cxy + by); |
|
|||
2.9. w = ax2 |
+ xy + y2 + i(bx2 + 2xy + cy2); |
||||
2.10. w = x3 |
+ axy2 + i(bx2y + cy3); |
|
|||
2.11. w = x2 |
+ ax + by2 + i(11y + cxy); |
; |
|||
2.12. w = x + x2 + y2 |
+ i by + x2 + y2 |
||||
|
|
ax |
|
cy |
|
91

2.13.w = a(x2 x2) + y3 + 5x2y + i(x3 + bxy2 + cxy);
2.14.w = x2 y2 + ax 7y + i(bx + 7y + cxy);
2.15.w = ax + by + cxy + i(x2 y2 + ay bx);
2.16.w = ax + 3y + bxy + i(x2 y2 + cx + 16y);
2.17.w = x3 + ax2y + 3xy2 y3 + i(bx3 + 3xy2 + cx2y + y3);
2.18.w = x3 + axy2 6xy + i(bx2y y3 + bx2 cy2);
2.19.w = ax2y + bx + y3 + i(cx3 3xy2 + 2y);
2.20.w = ax2y + 2bxy + y3 + i(x3 + bx2 + cxy2 4y2);
2.21.w = x2 + axy y2 + i(bx2 + cxy 4y2 5);
2.22.w = x2 + axy y2 + 5x + i(bx2 + cxy 3y2 + 5y);
2.23.w = ax2 + bxy 4y2 2y + i(3x2 + cxy 3y2 + 2x);
2.24.w = x3 + axy2 4y + i(bx2y y3 + cx);
2.25.w = ax2y + by3 + 2(x2 y2) + i(x3 3xy2 + cxy);
2.26.w = x3 + xy(a 3y) i(y2(y + 3) + x2(by + c));
2.27.w = axy + 7x + by + i(x2 y2 + 3x + cy);
2.28.w = ax2 10xy + 3y2 3y + i(bx2 6xy + cy2 + 3x);
2.29.w = ax2 + 2y(x y) + 3x y + i(x(4y x) + by2 + cx + 3y);
2.30.w = ax2y + y3 + 9x + i(x3 + bxy2 + cy).
3.Восстановить аналитическую в окрестности точки z0 функцию w = f(z) по известной действительной части u(x; y)
или мнимой v(x; y) и значению f(z0):
3.1. u = x3 3xy2 x, f(0) = 0;
3.2. u = x2 y2 + 5x + y y , f(1) = i; x2 + y2
x
3.3. u = x2 + y2 + x, f(1) = 2; 3.4. v = e y sin x, f(0) = 1;
y
3.5. v = 1 x2 + y2 , f(1) = 1 + i; 3.6. u = 1 sin y ex, f(0) = 1 + i; 3.7. v = 3x2y y3, f(0) = 1;
3.8. v = 3x2y y3 y, f(0) = 0; 3.9. v = x2 y2 + 2x + 1, f(0) = i;
92

3.10. v = ln(x2 + y2) + x 2y, f(1) = 1 + i;
y
3.11. v = (x + 1)2 + y2 , f(0) = 1;
3.12. v = e y sin x + y, f(0) = 1;
3.13. u = e2x + 1 cos y, f(0) = 2; ex
3.14.u = x3 3xy + 1, f(0) = 1;
3.15.v = ex(y cos y + x sin y), f(0) = 0;
3.16. v = 3 + x2 y2 |
y |
, f(1) = i; |
2(x2 + y2) |
3.17.u(x; y) = 2x3 6xy2 6xy + 4x; f( i) = 0;
3.18.v = ex cos y, f(0) = 1 + i;
3.19.v = 2(ch x sin y xy), f(0) = 0;
3.20.u = 2 sin y ch y x, f(0) = 0;
y
3.21. v = y x2 + y2 , f(1) = 2;
3.22. u = ex(x cos y y sin y), f(0) = 0;
3.23.v = e2x 1 sin y, f(0) = 2; ex
3.24.u = e y cos x + x, f(0) = 1; x + 1
3.25.u = (x + 1)2 + y2 , f(0) = 1;
3.26.v = y cos y ch x + x sin y sh x, f(0) = 0;
3.27.v = 2 cos x ch y x2 + y2, f(0) = 2;
3.28.u = ex(x cos y y sin y) + x3 3xy2 + y, f(0) = 1;
3.29.v = x2 y2 x, f(0) = 0;
3.30.v = y cos y ch x + x sin y ch x, f(0) = 0:
4.Восстановить аналитическую функцию w = f(z) по ее мнимой v(x; y) или действительной части u(x; y) и найти ее производную:
93

4.1. u = ex cos y +3x2y y3 3; |
4.16. v = 4x3y 4xy3 + 6xy; |
||||||||||||||||||||||||||||||||
4.2. v = 3x2y y3 3y; |
|
4.17. u = 2ex sin y 2y; |
|
|
|
||||||||||||||||||||||||||||
4.3. v = 4x y + 1; |
|
|
|
|
|
4.18. v = |
|
|
2y |
|
|
+ 3y; |
|
|
|
|
|||||||||||||||||
+ 3y 1; |
x |
2 |
+ y |
2 |
|
|
|
|
|
||||||||||||||||||||||||
4.4. v = 4x |
3 |
4xy |
3 |
|
|
|
|
+ 2x; |
|
|
|
|
|||||||||||||||||||||
|
|
|
4.19. u = x |
2 |
y |
2 |
|
|
|
|
|||||||||||||||||||||||
4.5. u = x2 |
|
y2 |
|
|
3x + 2; |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2y |
|
|
|
|
|
|
|
2 |
|
|
2 |
+ 2y; |
|
|
|||||||||||
4.6. |
v = x3 |
|
|
3xy2 |
|
|
|
|
; |
4.20. u = x + y |
|
|
|
||||||||||||||||||||
|
|
x2 + y2 |
|
cos x; |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
4.21. v = x + ch y |
|
|
|
||||||||||||||||||||||||
4.7. u = x sin x ch y y cos x sh y; |
4.22. u = |
|
|
3x |
|
|
|
|
|
|
|
|
5; |
|
|||||||||||||||||||
|
|
|
|
|
|
+ 5x |
|
||||||||||||||||||||||||||
x2 + y2 |
|||||||||||||||||||||||||||||||||
4.8. u = x + ex cos y; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4.9. u = x cos x ch y+y sin x sh y; |
4.23. u = 2ex sin y + 3x 2y; |
||||||||||||||||||||||||||||||||
4.10. v = 2xy + 3y |
4y |
; |
4.24. u = ln(x2 + y2) + 2x; |
||||||||||||||||||||||||||||||
x2 + y2 |
4.25. v = e3x cos 3y; |
|
|
|
|
|
|
||||||||||||||||||||||||||
4.11. v = 6xy + cos x sh y; |
|
4.26. u = x |
4 |
|
|
|
2 |
|
2 |
|
|
|
|
4 |
; |
|
|||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
6x y |
|
+ y |
|
|||||||||||||||
4.12. u = |
|
|
|
|
|
|
+ sin x ch y; |
4.27. v = ex sin y + 2xy + 5y; |
|||||||||||||||||||||||||
|
|
+ y2 |
|||||||||||||||||||||||||||||||
|
x2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
y |
+ e |
x |
sin y; |
||||||||||||||||
|
|
|
3 |
3xy |
3x; |
|
4.28. v = arctg x |
|
|||||||||||||||||||||||||
4.13. u = x |
|
|
4.29. |
v = x + ch y |
|
cos x |
; |
|
|
||||||||||||||||||||||||
4.14. u = x4 6x2y2 +y4 +x2 |
|
|
3 |
|
|
|
|
3 |
|
|
|
|
7y |
||||||||||||||||||||
y2 |
+ 3x + 5; |
|
|
|
|
|
|
|
|
|
|
4.30. v = 4x |
y 4xy |
|
|
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.15.v = arctg xy +ex sin y+3y;
5.Проверить гармоничность функции в указанной области и найти, если это возможно, аналитическую функцию поx + y
данной ее действительной или мнимой части:
x2 y2
5.1. u = (x2 + y2)2 , 0 < jzj < +1;
5.2. u = ln(x2 + y2) x2 + y2, 0 < jzj < +1;
5.3. u = ey=x, 0 < jzj < +1;
5.4. u = x3 3xy2, 0 6 jzj < +1;
5.5. v = 2ex sin y, 0 6 jzj < +1; 5.6. u = 2xy + 3, 0 6 jzj < +1;
5.7. v = xy, 0 6 jzj < +1;
5.8. u = x3 + 3x2y, 0 6 jzj < +1;
5.9. u = ex cos y, 0 6 jzj < +1;
5.10. u = y3 10xy2, 0 6 jzj < +1;
94

5.11.u = ln(x2 + y2) 2xy, 0 < jzj < +1;
5.12.u = ln(x2 + y2) + x2, 0 < jzj < +1;
5.13. v = |
|
x |
|
2xy, 0 < jzj < +1; |
|
|
||||||||||
x2 + y2 |
|
|
||||||||||||||
5.14. v = e x cos y, 0 6 jzj < +1; |
|
|
|
|
||||||||||||
5.15. v = x2 + 2xy y2, 0 6 jzj < +1; |
|
|
||||||||||||||
5.16. v = ey(cos x + sin y), 0 6 jzj < +1; |
|
|
||||||||||||||
5.17. u = x3 |
+ 2x2y y2, 0 6 jzj < +1; |
|
|
|||||||||||||
5.18. u = x3 |
+ 3xy, 0 6 jzj < +1; |
|
|
|
|
|||||||||||
5.19. u = ex ch y, 0 6 jzj < +1; |
|
|
|
|
||||||||||||
5.20. v = 2 sin x ch y + x2, |
0 6 jzj < +1; |
|
|
|||||||||||||
5.21. u = 2 cos x ch y + xy, |
0 6 jzj < +1; |
|
||||||||||||||
5.22. u = x3 |
+ y3, 0 6 jzj < +1; |
|
|
|
|
|||||||||||
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
5.23. u = x |
+ 3xyy 2x, 0 6 jzj < +1; |
|
|
|||||||||||||
5.24. v = xy |
|
|
, 0 < jzj < +1; |
|
|
|||||||||||
x2 + y2 |
|
; |
||||||||||||||
|
|
x |
sh y + x2 |
|
y2 |
|
0 |
z |
j |
< + |
1 |
|||||
5.25. v = sin x |
|
|
|
|
|
, |
|
6 j |
|
|
||||||
5.26. v = |
|
+ x2 + y2, 0 < jzj < +1; |
|
|||||||||||||
x2 + y2 |
|
|||||||||||||||
5.27. u = x2 |
y2 |
|
|
y |
|
, 0 < jzj < +1; |
|
|||||||||
x2 + y2 |
|
|||||||||||||||
5.28.u = 3x2y y3 + xy, 0 6 jzj < +1;
5.29.u = 2xy + 3y2 1, 0 6 jzj < +1;
5.30.v = ex(x cos y y + 1), 0 6 jzj < +1.
6.Найти коэффициент растяжения k и угол поворота ' для
заданного отображения w = f(z) в точке z0:
6.1. w = 5z2 4z + 3, z0 = 1 + 3i; p
6.2. w = z2 iz + 3i, z0 = 1 3i;
6.3.w = 3z2 4iz + i, z0 = i + 1;
6.4.w = z3 + 4z 3i, z0 = 2 i;
6.5.w = (z + 3i)2 4z, z0 = 2 + i;
95
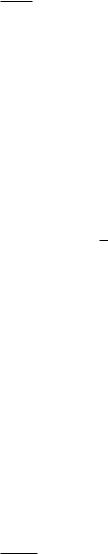
6.6. w = z2, z0 = i; |
|
|
|
|
|
|
|
|
|
6.19. w = z2 |
+ 4z, z0 = i; |
||||||||||||||||||||||||||||||||
6.7. w = sin z, z0 = 0; |
|
|
|
|
|
|
|
|
w = |
1 z |
|
z |
|
= |
|
|
|
i; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
6.20. |
1 + z , |
0 |
|
|
||||||||||||||||||||||||||||||||
6.8. w = 2z2 + z, |
z0 = i; |
|
|
|
|
|
|
|
i |
|
|
|
|||||||||||||||||||||||||||||||
|
|
1 + iz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6.9. w = |
, |
z0 = i; |
|
|
|
|
6.21. w = 2z3 iz + |
|
|
, |
z0 = i; |
||||||||||||||||||||||||||||||||
|
|
|
|
z |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
1 |
|
iz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.22. w = |
|
|
z |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6.10. w = z |
3 |
|
+ 2z, z0 = i; |
|
|
|
|
|
|
z0 = i + 1; |
|||||||||||||||||||||||||||||||||
|
|
|
2i; |
1 |
|
iz |
|||||||||||||||||||||||||||||||||||||
6.11. |
w = z2 |
|
+ 3z |
, |
z |
0 |
= 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
, |
|
|
|
|
|
|
|
6.23. w = |
|
|
2z |
|
, |
z0 = i 1; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + iz |
|||||||||||||||||||||
6.12. w = iz + 1 |
z0 = i + 1; |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
3 |
+3z |
2 |
1, z0 = 2i; |
||||||||||||||||||||||||||||||||||||||
|
|
|
1 + z |
|
|
|
|
|
|
|
|
|
|
|
|
|
6.24. w = z |
|
|
||||||||||||||||||||||||
6.13. w = |
|
|
|
|
|
|
, |
z0 |
= 2; |
|
|
|
|
6.25. w = z3 |
2z, z0 = i 1; |
||||||||||||||||||||||||||||
1 |
|
|
|
z |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
6.26. |
w = z3 |
|
|
z2 |
+ 3z |
, |
z |
0 |
= i; |
|||||||||||
|
|
|
|
|
|
|
z , |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
6.14. w = 2z |
|
|
|
|
|
2i; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
z0 = |
|
|
6.27. w = z |
|
|
|
|
+ 3z, z0 = i; |
||||||||||||||||||||||||||||||
|
|
|
|
2z+3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3z |
|
|||||||||||||||||||||||
6.15. w = e3 |
|
|
|
|
z0 |
|
= |
|
i; |
|
|
|
6.28. w = z3 5iz2+7i, z0 = 2i; |
||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||||||||
6.16. w = z |
|
|
|
2z, z0 = i; |
|
|
|
6.29. w = z2 |
|
3z + |
i |
, |
z0 = i; |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
6.17. w = 2z2 3z, |
|
z0 = 1 i; |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||||||||||||||||||||||||
6.18.w = z2 + 5z i, z0 = 3i; 6.30. w = ez, z0 = ln 2 + i 4 :
7.Найти множества всех точек z0, в которых коэффициент
линейного растяжения при отображении w = f(z) равен k:
7.1.w = (3 + 4i)z2 (1 + i)z, k = 1;
7.2.w = (1 i)z2 + (2 3i)z, k = 2;
7.3. w = z3 |
+ iz2, |
k = 0; |
|
|
1 |
, k = |
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
7.13. w = |
|
|
|
; |
|||
7.4. w = z2 |
+ iz + 4, k = |
; |
z |
2 |
||||||||||||||||||
|
7.14. w = (z + 3 2i)3, k = 2; |
|||||||||||||||||||||
2 |
||||||||||||||||||||||
7.5. w = (z + 2i 1)3, k = 3; |
7.15. w = z3, k = 1; |
|||||||||||||||||||||
7.6. |
w = z3 |
+ iz2 |
|
7i |
, |
k = 0; |
7.16. w = z2 |
+ z, |
k = 1; |
|||||||||||||
7.7. w = z3 |
iz2, k = 0; |
|
|
7.17. w = (z i)3, k = 1; |
||||||||||||||||||
7.8. w = iz3 + 3z2, k = 0; |
|
|
7.18. w = z2 |
2z, k = 2; |
||||||||||||||||||
7.9. |
w = iz2 |
|
3z |
, |
k = 2; |
|
|
7.19. w = z3 |
+ 3iz2, k = 0; |
|||||||||||||
7.10. w = z3 2z, k = 0; |
|
|
7.20. w = (3i+2)z2 iz, k = 2; |
|||||||||||||||||||
7.11. w = |
|
|
iz |
|
, |
k = |
1 |
; |
|
|
7.21. w = |
i |
, k = 1; |
|||||||||
|
|
12 iz |
|
|
|
2 |
|
|
|
|
z |
|
|
|
|
|
|
|||||
7.12. w = z |
+ 2z, k = 1; |
|
|
7.22. w = |
1 |
iz |
, |
|
k = 1; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ iz |
|
|||||
96

7.23. w = (z 3i)3, k = 2; |
7.28. w = (z 2 + i)3, k = 1; |
7.24. w = z2 + iz, k = 1; |
7.29. w = z3 iz2 + z, k = 0; |
7.25. w = iz2 + 4z 3i, k = 1; |
7.30. w = iz3 + 4z, k = 0. |
7.26.w = z3 + 2iz, k = 0;
7.27.w = z2 + 3iz, k = 12;
8.Найти множества всех точек z0, в которых угол поворота
при отображении w = f(z) равен ':
8.1.w = 5iz3 + (7 2i)z, ' = 0;
8.2.w = 3iz3 (4 3i)z, ' = 4 ;
8.3.w = (3 2i)z3 2iz, ' = 0;
8.4. w = z2 + 2z, ' = 2 ; 8.5. w = z1, ' = 2 ;
8.6. w = z1, ' = 0;
8.7. w = z3 3z, ' = 0; 8.8. w = z3 + 2z, ' = 2 ;
8.9. w = z3 3z, ' = 2 ; 8.10. w = z3 + 9z, ' = 0;
8.11. w = z2 + iz, ' = 0;
8.12. w = iz3 + 3z, ' = 4 ;
8.13. w = 3z2 +(2i 1)z, ' = 0;
8.14. w = iz3 2z2, ' = 0;
8.15. w = 4z2 +(3i 2)z, '= 2 ;
8.16. w = iz3 + 4z2, ' = 2 ; 8.17. w = iz3 + 4z, ' = 0;
97

Решение типового варианта
Пример 1. Исследовать функцию на дифференцируемость и аналитичность, в случае аналитичности функции w, найти ее производную, если a) w = z2 5iz + i Im z + Re z2;
б) w = z2 + (7 + 2i)z 5 + 9i:
Решение. a) запишем комплексное число z в алгебраической форме, и отделим действительную u(x; y) и мнимую v(x; y) части функции w(z).
w(z) = (x + iy)2 5i(x iy) + i Im(x + iy) + Re(x iy)2; w(z) = x2 + 2ixy y2 5ix 5y + iy + Re(x2 2ixy y2); w(z) = x2 + 2ixy y2 5ix 5y + iy + x2 y2;
w(z) = 2x2 2y2 5y + i(2xy 5x + y);
значит, u(x; y) = 2x2 2y2 5y; v(x; y) = 2xy 5x + y: Функции u(x; y), v(x; y) непрерывно дифференцируемы на R2. Проверим выполнение условий Коши-Римана (3:4):
u0x = (2x2 2y2 5y)0x = 4x, vx0 = (2xy 5x + y)0x = 2y 5;
u0y = (2x2 2y2 5y)0y = 4y 5; vy0 = (2xy 5x + y)0y = 2x + 1:
ux0 |
= vy0 ; |
|
4x = 2x + 1; |
|
x = 1=2; |
||
u0 |
= v0 |
; |
4y |
|
5 = 2y |
|
5; y = 0: |
y |
x |
|
|
|
|
||
Следовательно, искомая функция дифференцируема только в точке z0 = 1=2: Поскольку в любой проколотой окрестности точки z0 функция w не дифференцируема, то она нигде не аналитична.
б) w = (x + iy)2 + (7 + 2i)(x + iy) 5 + 9i;
w= x2 + 2ixy y2 + 7x + 2ix + 7iy 2y 5 + 9i;
w= (x2 y2 + 7x 2y 5) + i(2xy + 2x + 7y + 9);
u(x; y) = x2 y2 + 7x 2y 5; v(x; y) = 2xy + 2x + 7y + 9:
Функции u(x; y), v(x; y) непрерывно дифференцируемы на
R2. Проверим выполнение условий Коши-Римана (3:4):
u0x = (x2 y2 + 7x 2y 5)0x = 2x + 7, vx0 = (2xy + 2x + 7y + 9)0x = 2y + 2;
98
u0y = (x2 y2 + 7x 2y 5)0y = 2y 2; vy0 = (2xy + 2x + 7y + 9)0y = 2x + 7:
u0x = vy0 ; 2x + 7 2x + 7;
u0y = vx0 ; 2y 2 (2y + 2);
для всех (x; y) из R2, следовательно, функция w = z2 + (7 + 2i)z 5 + 9i
дифференцируема, а значит, и аналитична во всей комплексной плоскости.
w0 = u0x + ivx0 = 2x + 7 + i(2y + 2) = 2z + 7 + 2i:
Пример 2. Найти значения постоянных a; b; c, при которых функция w = ax2 + 3y2 + b cos x sh y + i(cxy + sin x ch y)
будет аналитической в C.
Решение.
u(x; y) = Re w(z) = ax2 + 3y2 + b cos x sh y; v(x; y) = Im w(z) = cxy + sin x ch y:
Вычислим частные производные функций u(x; y), v(x; y):
u0x = (ax2 + 3y2 + b cos x sh y)0x = 2ax b sin x sh y; vx0 = (cxy + sin x ch y)0x = cy + cos x ch y;
u0y = (ax2 + 3y2 + b cos x sh y)0y = 6y + b cos x ch y; vy0 = (cxy + sin x ch y)0y = cx + sin x sh y:
Согласно условиям Коши-Римана (3:4), получаем:
2ax b sin x sh y cx+sin x sh y; cy+cos x ch y (6y+b cos x ch y);
значит, при a = 3, b = 1, c = 6 функция w является аналитической во всей комплексной плоскости.
99

Пример 3. Восстановить аналитическую в окрестности точки z0 функцию w = f(z) по известной мнимой части v(x; y) и значению f(z0), если v(x; y) = 2xy sin x sh y, f(0) = 2.
Решение. Для определения действительной части функции w = f(z) воспользуемся условиями Коши-Римана (3:4). Так как
@y@v = (2xy sin x sh y)0y = 2x sin x ch y;
то согласно первому условию @u@x = 2x sin x ch y: Интегрируем последнее равенство по x, получим:
Z
u = (2x sin x ch y)dx = x2 + cos x ch y + '(y): (3.11)
Используем второе из условий (3:4). Так как
|
@v |
|
= (2xy |
|
sin x sh y)0 |
= 2y |
|
cos x sh y; |
|
@x |
|
||||||||
|
x |
|
|
|
|||||
то |
|
|
|
|
|
|
|
||
|
@u |
= (2y cos x sh y) = cos x sh y 2y: |
(3.12) |
||||||
|
@y |
|
|||||||
Продифференцируем функцию u(x; y) из (3.11) по переменной y:
@u = (x2 + cos x ch y + '(y))0 = cos x sh y + '0(y): (3.13)
@y |
y |
|
Из равенств (3.12), (3.13) получаем:
cos x sh y 2y = cos x sh y + '0(y);
откуда '0(y) = 2y, значит, '(y) = y2 + C; а искомая функция u(x; y) имеет вид: u(x; y) = x2 y2 +cos x ch y +C: Функция
100

w = f(z) = x2 y2 + cos x ch y + C + i(2xy sin x sh y): Воспользуемся начальным условием: f(0) = 2:
f(0) = 02 02 +cos 0 ch 0+C +i(0 sin 0 sh 0); f(0) = 1+C = 2,
откуда C = 1, следовательно, |
|
|
|
|
|
|||||||||
|
|
|
w = f(z) = x2 y2 + cos x ch y + 1 + i(2xy sin x sh y): |
|||||||||||
|
|
|
Пример |
4. |
Восстановить |
|
|
аналитическую |
функцию |
|||||
w = f(z) по |
ее |
|
действительной |
|
части u(x; y) и |
найти ее |
||||||||
производную, если u(x; y) = 3x + x2 y2 + 5e2x sin 2y. |
||||||||||||||
|
|
|
|
Решение. Вычислим частные производные функции |
||||||||||
u(x; y) по переменным x; y: |
|
|
|
|
|
|||||||||
@u |
= (3x + x2 y2 + 5e2x sin 2y)x0 |
= 3 + 2x + 10e2x sin 2y; |
||||||||||||
|
|
|
||||||||||||
|
@x |
|||||||||||||
@u |
= (3x + x2 |
|
y2 + 5e2x sin 2y)0 |
= |
|
2y + 10e2x cos 2y: |
||||||||
|
@y |
|
||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
||||
|
|
|
С учетом (3:4) получаем: |
|
|
|
|
|
||||||
|
|
|
|
@v |
|
|
|
@v |
|
|
|
|||
|
|
|
|
|
= 3 + 2x + 10e2x sin 2y; |
|
= 2y 10e2x cos 2y: (3.14) |
|||||||
|
|
|
@y |
@x |
||||||||||
Интегрируя первое равенство из (3.14) по переменной y, получим:
Z
v = (3 + 2x + 10e2x sin 2y)dy = 3y + 2xy 5e2x cos 2y + '(x):
Вычислим производную функции v(x; y) по переменной x:
@x@v =(3y+2xy 5e2x cos 2y+'(x))0x =2y 10e2x cos 2y+'0(x): (3.15)
Приравнивая (3.14) и (3.15), получаем:
2y 10e2x cos 2y = 2y 10e2x cos 2y + '0(x);
откуда '0(x) = 0; '(x) = C, где C 2 R: Значит, аналитическая функция w = u + iv имеет вид:
101
w = 3x + x2 y2 + 5e2x sin 2y + i(3y + 2xy 5e2x cos 2y + C); или w = 3(x + iy) + (x + iy)2 + 5e2x(sin 2y i cos 2y) + iC = = 3z + z2 5ie2z + iC:
Производную функции w = f(z) вычислим по формуле:
w0 = u0x + ivx0 :
w0 = 3 + 2x + 10e2x sin 2y + i(2y 10e2x cos 2y); w0 = 3 + 2(x + iu) 10ie2x(cos 2y + i sin 2y); w0 = 3 + 2z 10ie2z;
или, используя таблицу производных:
w0 = (3z + z2 5ie2z + iC)0 = (3z)0 + (z2)0 (5ie2z)0 + (iC)0 = = 3 + 2z 5i 2e2z + 0 = 3 + 2z 10ie2z:
Пример 5. Проверить гармоничность функции в указанной области, и найти, если это возможно, аналитическую функцию по данной ее мнимой части:
а) v(x; y) = x3 + 8x2y; 0 6 jzj < +1;
б) v(x; y) = x4 6x2y2 + y4 + 2xy; 0 6 jzj < +1:
Решение. а) Проверим гармоничность функции v(x; y): Вычисляем:
vx0 = (x3 +8x2y)0x = 3x2 +16xy, vy0 = (x3 + 8x2y)0y = 8x2; vxx00 = (3x2 +16xy)0x = 6x+16y; vyy00 = (8x2)0y = 0:
Функция v(x; y) имеет непрерывные частные производные второго порядка, но не удовлетворяет в области D = R2 уравнению Лапласа (3.6), следовательно, не будет гармонической в указанной области, и не является мнимой частью некоторой аналитической функции.
б) Вычисляем частные производные первого и второго порядка функции v(x; y) = x4 6x2y2 + y4 + 2xy; 0 6 jzj < +1:
v0 |
= 4x3 |
|
12xy2 + 5y, |
v0 |
= 12x2y + 4y3 + 5x; |
|||||||
x |
|
|
|
|
|
|
y |
|
|
|
||
v00 |
|
= (12x2 |
|
12y2 |
; |
v00 |
|
= |
12x2 |
+ 12y2: |
||
xx |
|
|
|
|
|
yy |
|
|
|
|||
102
Функция v(x; y) имеет непрерывные частные производные второго порядка, и в области D = R2 удовлетворяет уравнению
Лапласа
vxx00 + vyy00 = 0;
следовательно, функция v(x; y) является гармонической в указанной области, значит, является мнимой частью некоторой аналитической функции w = f(z). Действительную часть u(x; y) функции w найдем, используя условия Коши-Римана (3:4). Значит,
u0 |
= 12x2y + 4y3 |
+ 5x; u0 |
= |
|
4x3 |
+ 12xy2 |
|
5y: |
(3.16) |
x |
|
y |
|
|
|
|
Интегрируя первое равенство из (3.16) по переменной x, получаем:
Z
u(x; y) = ( 12x2y + 4y3 + 5x)dx = 4x3y + 4xy3 + 52x2 + '(y):
Дифференцируем найденную функцию u по переменной y. u0y = 4x3 + 12xy2 + '0(y):
С учетом (3.16) получим
4x3 + 12xy2 + '0(y) = 4x3 + 12xy2 5y;
откуда '0(y) = 5y, '(y) = 52y2 + C, C 2 R: Искомая аналитическая функция f(z) имеет вид:
w = u+iv = 4x3y+4xy3+52x2 52y2+C+i(x4 6x2y2+y4+2xy):
Пример 6. Найти коэффициент растяжения k и угол поворота ' для отображения w = z3 iz2 + 2z в точке z0 = 1 + 2i:
Решение. Имеем: w0 = 3z2 2iz + 2:
w0(1+2i) = 3(1+2i)2 2i(1+2i)+2 = 3(1+4i 4) 2i 4i2+2 =
103

= 3 + 12i 12 2i + 4 + 2 = 3 + 10i:
Перейдем от алгебраической формы записи полученного
комплексного числа к тригонометрической. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
w0 |
|
w0(1 + 2i) = |
|
|
|
|
|
|
|
|
|
= p |
|
: |
|
|
|
|
|||||||||||||
j |
(z0) = |
( |
|
3)2 |
+ 102 |
109 |
|
|
|
|
||||||||||||||||||||||
|
j |
j |
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
arg w0(1 + 2i) = '; |
|
где |
pcos ' = |
|
|
3 |
|
; |
|
|
sin ' = |
10 |
: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Угол |
|
|
лежит |
|
во |
|
|
|
|
|
|
p109 |
|
|
|
p109 |
||||||||||||||||
' |
|
|
|
второй |
|
|
четверти, |
значит |
||||||||||||||||||||||||
arg w0(1 + 2i) = |
|
arcsin |
10 |
|
: Таким образом, |
коэффи- |
||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
p109 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
циент |
растяжения |
k |
= |
|
jw0(z0)j = |
109, а |
угол |
поворота |
||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
' = |
arg w0(z0) = |
|
|
arcsin |
|
10 |
|
|
в |
точке |
z0 = 1 + 2i при |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
p109 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
отображении w = z3 iz2 + 2z:
Пример 7. Найти множества всех точек z, в которых коэффициент линейного растяжения при отображении w = (z 5 + 2i)3 равен k.
Решение. Множество всех точек z, в которых коэффициент линейного растяжения равен k, удовле-
творяет условию: |
jw0(z)j = k: |
Вычислим |
производную: |
w0 = ((z 5 + 2i)3)0 |
= 3(z 5 + 2i)2: |
Запишем |
комплексное |
число z в алгебраической форме z = x + iy; тогда
w0 = 3(x + iy 5 + 2i)2 = 3 ((x 5) + i(y + 2))2 ;
w0 = 3(x 5)2 + 6(x 5)(y + 2)i 3(y + 2)2;
jw0(z)j = p(3(x 5)2 3(y + 2)2) + 36(x 5)2(y + 2)2;
откуда jw0(z)j2 = k2; значит,
9(x 5)4 18(x 5)2(y + 2)2 + 9(y + 2)4 + 36(x 5)2(y + 2)2 = k2;
9(x 5)4 + 18(x 5)2(y + 2)2 + 9(y + 2)4 = k2; |
|
|
|
9 (x 5)2 + (y + 2)2 2 = k2; (x 5)2 + (y + 2)2 = |
k |
: |
|
|
|
||
3 |
|||
104

|
|
Следовательно, искомое множество есть окружность с цен- |
||||||||||||||||||||||||||||||||
тром в точке z0 = 5 2i радиуса R = r |
|
|
: jz 5 + 2ij = r |
|
|
|||||||||||||||||||||||||||||
3 |
3 : |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
Пример 8. Найти множества всех точек z, в которых угол |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поворота при отображении w = iz3 + (3 |
4i)z |
|
равен |
|
. |
|
|
|||||||||||||||||||||||||||
|
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
Решение. Множество всех точек z, в которых угол поворо- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
та при отображении w = iz3 + (3 4i)z равен |
|
, удовлетворяет |
||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||
условию: arg w0(z) = |
|
: Вычислим производную: |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
w0 = 3iz2 + 3 4i = 3i(x + iy)2 + 3 4i = |
|
|
|
|
||||||||||||||||||||||||||
|
= 3i(x2 + 2xyi y2) + 3 4i = 6xy + 3 + i(3x2 3y2 4): |
|||||||||||||||||||||||||||||||||
j |
0 |
j |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
, где |
|
|
|||
= |
(3 6xy) |
|
|
|
+ (3x |
|
|
2 |
|
|
2 |
|
|
|
|
(z) = ' |
|
|
||||||||||||||||
|
w |
(z) |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
3y2 |
|
4)2; arg w |
|
|
|
|
|||||||||||||
|
|
|
|
|
sin ' = |
|
|
|
|
|
|
|
|
|
3x |
|
3y |
|
4 |
|
|
|
|
; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
p(3 6xy)2 + (3x2 3y2 4)2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
cos ' = |
p |
|
|
|
|
3 6xy |
|
|
|
|
|
|
: |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
(3 6xy)2 + (3x2 3y2 4)2 |
|
|
|
|
|||||||||||||||||||
Учитывая, что ' = |
|
|
, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
p
3x2 3y2 4 = (3 6xy)2 + (3x2 3y2 4)2; 3 6xy = 0;
откуда 2xy = 1: Таким образом, искомое множество есть гипербола Im z2 = 1.
105
