Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гродненский государственный университет им. Я. Купалы

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ТФКП Детченя, Кулеш, Пецевич, Романовский.pdf

Скачиваний:

252

Добавлен:

18.02.2016

Размер:

18.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1714 15 16 17 > Следующая >>>

4.8. Тригонометрические функции

Перейдем к тригонометрическим функциям. Для действительных значений x из формулы Эйлера (1.12) следует, что

eix = cos x + i sin x; e ix = cos x i sin x:

Отсюда cos x =

eix + e ix

, sin x =

eix e ix

. Эти формулы

служат основой следующего определения.

Тригонометрические функции комплексного переменного z

определяются равенствами:

cos z =

eiz + e iz

;

sin z =

eiz e iz

;

(4.23)

tg z =

sin z

;

ctg z =

cos z

sin z

Определенные таким образом функции сохраняют многие свойства тригонометрических функций действительного переменного. Из периодичности функции ez следует, что функции sin z и cos z периодичны с периодом 2 , a tg z и ctg z с периодом . Функция sin z нечетна, a cos z четна, Действительно,

sin(	z) =	e iz e i( z)	=	eiz e iz	=	sin z:
		2i		2i
Аналогично доказывается			четность функций cos z. Для

функций, определенных равенствами (4.23), справедливы обычные тригонометрические соотношения. Например,

sin2 z + cos2 z = 1;		sin(z1 + z2) = sin(z1) cos(z2) + cos(z1) sin(z2);
и т.д. Докажем, например, последнюю формулу:
	sin(z1) cos(z2) + cos(z1) sin(z2) =
= eiz1 e iz1		eiz2 + e iz2	+ eiz1 + e iz1		eiz2	e iz2	=
	2i	2		2		2i

136

= ei(z1+z2) e i(z1+z2) = sin(z1 + z2): 2i

Функции sin z и cos z аналитичны во всей плоскости C, причем имеют место обычные формулы дифференцирования:

(sin z)0 = cos z;

(cos z)0 = sin z:

Например, для sin z имеем:

(sin z)0 =

eiz e iz

(eiz)

iz)

ieiz + ie iz =

eiz + e iz = cos z:

Используя формулы для производной частного, получим

(tg z)0 =	1		(ctg z)0	1
		;		=		:
	cos2 z				sin2 z

Однако не все свойства тригонометрических функций действительного переменного сохраняются при продолжении этих функций в комплексную плоскость. В частности, sin z и cos z могут принимать значения, по модулю превосходящие 1. Например,


cos i =	ei2 + e i2		=	e 1 + e1		1; 54; sin i =	e 1 e1	1; 17i:
							2i
2			2
Заметим,		что функция			w	= cos z является композици-

ей показательной функции w1 = eiz и функции Жуковского

	1	w1	1		. Следовательно функция w = cos z осуществ-
w =			+
	2			w1

ляет взаимно однозначное отображение полосы 0 6 Re z 6 на полную плоскость w с разрезами по лучам действительной оси [1; 1] и [1; 1].

137

Функции, обратные (4.23), называются обратными тригонометрическими функциями. Так как тригонометрические функции (4.23) периодичны, то обратные к ним функции будут бесконечнозначными. В силу того, что функции (4.23) достаточно просто выражаются через показательные, обратные к ним функции удается выразить через логарифмы. Получим такое выражение, например, для w = Arccos z. Из определения этой функции имеем:

z = cos w = eiw + e iw ; 2

откуда e2iw 2zeiw + 1 = 0. Решая это квадратное уравнение p

относительно eiw, находим eiw = z + z2 1 (мы опускаем перед знаком квадратного корня, поскольку понимаем корень как двузначную функцию, принимающую оба соответствующие значения). Из последнего равенства получаем

w = Arccos z = i Ln(z + z2 1): (4.24)

Аналогичные формулы можно дать и для других обратных тригонометрических функций:


	1 1			+ izp				(4.25)
							1 z2);
Arcsin z = i Ln(iz +
Arctg z =		Ln				;		(4.26)
	2i		1	iz
Arcctg z =	1	Ln	iz		1	:		(4.27)
	2i		iz +		1

Из элементарных функций комплексного переменного отметим также гиперболические функции sh z, ch z, th z и cth z,

определяемые равенствами:

sh z =

ez e z

; ch z =

ez + e z

;

(4.28)

sh z

ez e z

ch z

ez + e z

th z =

;

cth z =

sh z

ch z

ez + e z

ez e z

138

Они весьма просто выражаются через тригонометрические функции

sh z = i sin(iz); ch z = cos(iz); th z = i tg(iz); cth z = i ctg(iz);

и поэтому несущественно отличаются от последних.

4.9.Общие свойства конформных отображений

Впредыдущих разделах мы рассматривали некоторые элементарные функции и осуществляемые ими конформные отображения. Возникает вопрос: можно ли осуществить взаимноод-

нозначное конформное отображение произвольной области D на произвольную область D0? Используя непрерывность кон-

формного отображения нетрудно убедиться, что ответ на этот вопрос, вообще говоря, отрицательный. Например, многосвязную область нельзя взаимнооднозначно и непрерывно отобразить на односвязную. Для односвязных областей имеет место следующая теорема.

Теорема 4.5 (Теорема Римана). Пусть D и D0 односвязные области на расширенных плоскостях переменных z и w соответственно, причем границы этих областей состоят более чем из одной точки. Тогда существует аналитиче-

ская функция, взаимно-однозначно и конформно отображающая D на D0.

Из теоремы Римана следует, что односвязную область D нельзя конформно отобразить на единичный круг jwj < 1 только в двух случаях:

а) если D есть вся расширенная плоскость C (граница пустое множество);

б) если D есть расширенная плоскость, из которой удалена одна единственная точка (например, если D конечная плоскость C, когда из C удалена точка z = 1).

139

Отображение w = f(z) области D на D0, существующее по теореме Римана, не является единственным. Для однозначного определения конформного отображения нужно задать дополнительные условия, называемые условиями нормировки, содержащие три действительных параметра. Например, достаточно в какой-либо одной точке z0 области D задать значения

w0 = f(z0); = arg f0(z0):

(4.29)

Здесь в качестве параметров выступают две координаты точки w0 и действительное число . Условия (4.29) означают, что отображение w = f(z) является единственным, если для какойлибо точки z0 области D задать ее образ w0 в области D0 и угол поворота бесконечно малых векторов в точке z0.

Можно задавать и другие условия нормировки, отличные от (4.29). Например, задают образы одной внутренней и одной граничной точек области D:

f(z0) = w0; f(z1) = w1;

где z0, w0 внутренние точки областей D, D0; z1, w1 граничные точки этих областей. Здесь также присутствуют три действительных параметра: две координаты точки w0 и положение граничной точки wl, которая определяется одним действительным числом (например, расстоянием, отложенным по границе D0 от некоторой фиксированной граничной точки). Укажем еще один вариант условий нормировки:

f(zk) = wk; k = 1; 2; 3;

где zk и wk граничные точки областей D и D0.

Отметим, что для функции (4.10), конформно отображающей единичный круг jzj < 1 в единичный круг jwj < 1, тремя действительными параметрами являются координаты точки z0 и число .

140

Сформулируем следующее общее свойство конформных отображений.

При взаимно-однозначном и конформном отображении областей D и D0 сохраняется направление обхода их границ.

Другими словами, если при обходе границы область D остается слева, то и при соответствующем обходе границы области D0 эта область остается слева.

Большое значение для практики конформных отображений имеет принцип соответствия границ. Пусть односвязные области D и D0 ограничены кривыми и 0. Пусть, далее, функция w = f(z), аналитическая в D и непрерывная в D, отображает взаимнооднозначно на 0, причем, когда точка z обходит контур так, что область D остается слева, соответствующая точка w обходит контур 0 так, что область D0 также остается слева. Тогда функция w = f(z) осуществляет взаимно-однозначное конформное отображение области D на область D0.

Следовательно, для отыскания области, на которую функция w = f(z) отображает заданную область D, достаточно обойти границу области D и найти контур, на который эта граница отображается функцией f(z).

В заключение приведем еще одно общее свойство принцип сохранения области. Если функция w = f(z) аналитична в области D и отлична от постоянной, то множество D0, на которое она отображает D, также является областью (т.е. открытым связным множеством).

Пример 4.8. Отобразить область D, заключенную между
p			p
двумя окружностями M : jz 1j = 2 и N : jz + 1j =			2

конформно на верхнюю полуплоскость.

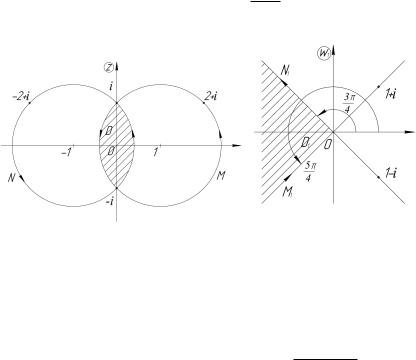
Решение. Указанные окружности пересекаются в точках i и i (рис. 4.19). Отобразим вначале область D в угол с вершиной в начале координат. Для этого нужно каждую из окружно-

141

стей, ограничивающих область D, отобразить в прямую, про-

z + i

ходящую через 0. Отображение w1 = z i переводит точку i в

1, а точку i в 0. Для уточнения уравнений прямых, в кото-

Рис. 4.19	Рис. 4.20

рые перейдут окружности M и N, найдем образы точек 2 + i и 2 + i, лежащих на соответствующих окружностях.

(2 + i) =

2 + i + i

= 1 + i; w

(

2 + i) =

2 + i + i

= 1

2 + i

Значит, M1 : Im w1 = Re w1, N1 : Im w1 = Re w1. При обходе точек i, 2 + i, i в плоскости z внутренность окружности M остается слева. При обходе их образов 0, 1 + i, 1 в плоскости w1 слева остается область Im w1 > Re w1. Аналогично, можно показать, что внутренность окружности N переходит в область

Im w1			< Re w1. Таким образом, область D перейдет в угол
D1 :			3	< arg w1	<	5	рис. 4.20. Повернув данный угол на
		4
	3				4
							3
		с помощью отображения w2 = e							iw1, получим область
								4
	4
D2 : 0 < arg w1 <					(рис. 4.21). Далее с помощью отображения

		2

142

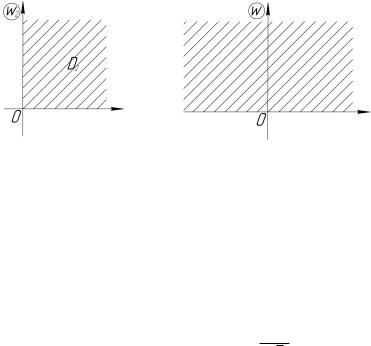
w = w22 область D2 перейдет в верхнюю полуплоскость (рис. 4.22). Составим композицию указанных выше отображений:

3 z + i

z + i

w = e

= e

= i

z i

Рис. 4.21

Рис. 4.22

Задания для аудиторных занятий к § 4

1. Указать геометрический смысл следующих преобразований.

1) w = z + 4; 2) w = z + 2i; 3) w = iz; 4) w = 3z;
	p		i	!z;		1p2

5) w =	3	+			6) w =		i	z + i:
	2		2

2.Найти функцию, отображающую треугольник с вершинами в точках 0, 1, i плоскости z в треугольник с вершинами 1 + i, 0, 2 плоскости w.

3.Найти линейное преобразование, оставляющее точку 1+i неподвижной, и переводящее точку i в точку 2 i.

4.Найти линейное преобразование, переводящее точки 0, 1 i в точки i, 3 2i соответственно.

143

5. Для указанных преобразований найти неподвижную точку z0 (если она существует), угол поворота вокруг нее и коэффициент растяжения.

1) w = 3z + 2 i; 2) w = iz + 1; 3) w = z + 1 2i:

6.Найти образ множества jz 1 + ij = 1 при отображении w = (2 + 5i)z 3 + 2i:

7.Найти общий вид линейного преобразования, отображающего

1) верхнюю полуплоскость в себя;

2) верхнюю полуплоскость на нижнюю полуплоскость;

3) верхнюю полуплоскость на правую полуплоскость; 4) полосу 0 < Re z < h в себя;

5) полосу 0 < Im z < h в себя;

6) полосу Re z < Im z < Re z + 1 в себя.

8.Найти линейную функцию, отображающую на полосу 0 < Re w < 1 при указанной нормировке, следующие множества (все параметры действительные, h > 0, b > 0, b2 > b1).

1) a < Re z < a + h, w(a) = 0; 2) a < Im z < a + h, w(ai) = 0;

3) k Re z < Im z < k Re z + b, w(0) = 0;

4) k Re z + b1 < Im z < k Re z + b2; w(ib1) = 0:

9. Указать геометрический смысл следующих отображений, раскладывая их на элементарные преобразования.

1) w =	(1 + i)z 4	;	2) w =	3iz + 1 5i	;
1) w =	z 3 + i	;	2) w =	z 2	;
	z 3 + i			z 2
3) w =	(3 + 4i)z + 5 4i		:
	z i

10.Найти дробно-линейное отображение, переводящее единичный круг jzj < 1 на нижнюю полуплоскость так, чтобы точки 1, i, 1 перешли соответственно в точки 1, 0, 1.

11.Найти дробно-линейное отображение, переводящее верхнюю полуплоскость на единичный круг так, чтобы точки1, 0, 1 переходили соответственно в точки 1, i, 1.

144

12. Найти дробно-линейное преобразование, переводящее точки z1, z2, z3 в точки w1, w2, w3 соответственно, если:

1 + i

1 + 2i

1 + i

1 + i 3 2i 8 + 6i 2 i 1 + 4i 2 + 3i:

13. Найти образы указанных областей при соответствую-

щих отображениях.

2iz

1) M : jz 1j < 2, w =

;

z + 3

2) M : jz + 1 + ij < 1, w =

iz + 2i

;

z 1 + i

3) M : jz ij < 2, w =

(3 + 4i)z + 1

;

z 2 i

4) M : 1 < jzj < 2, w =

z + 1

;

z + 2

M :

1 < Re z < 1

w =

z 1

;

z + 1

M :

< 1; Im z > 0

w =

2z i

iz + 2;

7) M : 0 < arg z <

w =

;

i < p

;

< p

w =

z 1

M :

z + i

z + 1

14. Отобразить верхнюю полуплоскость конформно на единичный круг так, чтобы точка 2i перешла в центр круга и

arg w0(2i) =

15. Отобразить единичный круг конформно на себя так,

чтобы

2 .

= 0

arg w

i 1

16. Отобразить конформно единичный круг jzj < 1 на верхнюю полуплоскость так, чтобы точка 0 перешла в точку 1 + i.

145

17. Найти функцию, отображающую первый квадрант

0 < arg z <

на круг jwj < 1 так, чтобы точкам

1 + i и 0 отве-

чали соответственно точки 0 и 1.

18. Отобразить сектор

< arg z <

, jzj < 2 конформно

на единичный полукруг jwj < 1, Im z

> 0

19. Отобразить угол 0 < arg z <

конформно на единич-

ный круг так, чтобы точка z1 = ei 6

перешла в центр круга

w1 = 0, а точка z2 = 0 в точку w2 = 1.

20. Найти образ области jzj < 1; 0 < arg z <

при отобра-

жении w = z2 + 1.

21. Найти функцию, отображающую область

< arg z <

на область 0 < arg w < 4 .

22. Отобразить конформно на верхнюю полуплоскость следующие области:

1)плоскость с разрезом по отрезку [ 1; 1];

2)плоскость с разрезом по отрезку [i; 3i];

3)плоскость с разрезами по лучам Im z = 0; 1 < Re z 6 a

иIm z = 0; b 6 Re z < +1; a < b;

4) jzj < 1, Im z > 0;			8) jzj < 1, jz + ij < 1;
5) jzj > 2, Im z > 1;			9) jzj < 1, jz + ij > 1;
6)	jzj > 1, Im z > 1;		10)	jzj > 1, jz + ij < 1;
7)	p	p	11)	jzj > 1, jz + ij > 1.
	jzj > 2, jz 2j <	2;

23.Найти функцию, отображающую горизонтальную полосу 0 6 Re z < +1, 0 6 Im z 6 на верхний полукруг jwj < 1,

Im w > 0.

24.Найти образ области D при отображении w, если


1) D : 0 < Im z < 2 ; Re z > 1, w = ez;
2) D : 0 < Im z <		; Re z < 0, w = e2z;

3)	4		w = ln z;
	D : r 6 jzj 6 R; 0 6 arg z 6 ,
4)	D : 1 < jzj < e; 0 < arg z < e,		w = ln z + 1.

146

	25.	Найти функцию	отображающую	полуполосу
0	< Im z < ; Re z > 0 на полуплоскость Im w > 0.
	26.	Найти функцию, отображающую область, ограничен-
ную окружностями jz 1j			= 1, jz 2j = 2,	на полосу
0	< Re w < 1.

27.Найти дробно-линейную функцию, отображающую область z + 1 > 1, jz + 2j < 2 на полосу 0 < Im w < 1.

28.Найти функцию, отображающую область, ограниченную окружностями jz 1j = 1, jz + ij = 1, на полуплоскость

Im w > 0.									1

29.	Отобразить круг jzj < 1 с разрезом по отрезку 1;
										4
на круг jwj < 1, то есть устранить разрез.
30.	Отобразить	на	верхнюю		полуплоскость				полосу
0 < Re z < 1 с разрезом			по лучу	Re z =		1	,	a 6 Im z < 1,
						2
a > 0.	Отобразить область jzj >			1,				i на	полосу
31.					Im z	>
0 < Re w < 1.		область jzj > 2,				> 2 на
32.	Отобразить				Re z				полосу

0< Im w < .

33.Записать в алгебраическом виде комплексные числа:

1)	Ln(1 + 2i);	5)	(1 + i)2+i;
2)	Ln(2 5i);	6)	5 2i;
3)	Ln( 1 + i);	7) ( 2 + 2i)i+1.
4) ii;		7) ( 2 + 2i)i+1.

34. Записать в алгебраическом виде решения уравнений:

1)	sin 2z = 8;	5)	tg z = 2 + 7i;
2)	sin 3z = 3i;	6)	tg iz = i;
3)	cos z = i;	7)	ctg z = 1 2i;
4)	cos 2z = 4;	8)	ctg 2z = 1 i.

147

ИДЗ 4

1. Найти образ множества M при линейном отображении

w = az + b, разложив его на элементарные

преобразования.

Указать геометрический смысл каждого преобразования.

1.1. w = (3 2i)z + 2 4i,

M : jz 1 + ij = 2;

1.2. w = ( 1 + 5i)z + 3 2i,

M : jz + 2 3ij = 1;

1.3. w = (5 5i)z 1 + 3i,

M : jz 1 2ij = 3;

1.4. w = ( 2 + 4i)z + 2i,

M : jz 2j = 4;

1.5. w = ( 3 + 2i)z 4 5i,

M : jz + 1 + 3ij = 1;

1.6. w = ( 3 3i)z + 4 + 5i,

M : jz 2 ij = 2;

1.7. w = (1 + 5i)z 2 6i,

M : jz 4 + 3ij = 2;

1.8. w = (4 2i)z + 1 2i,

M : jz 1 + 2ij = 3;

1.9. w = (3 i)z + 1, M : jz 2 ij = 4;

1.10. w = ( 3 + 4i)z 2 i,

M : jz 1 ij = 1;

1.11. w = 3iz + 2 5i,

M : 0 < Re z < 2;

1.12. w = (2 + 2i)z 4 2i,

M : 1 < Im z < 1;

1.13. w = 2iz + 1 3i,

M : Re z > 5;

1.14. w = 3z + 5 2i,

M : 2 < Im z < 3;

1.15. w = ( 3 + 3i)z 1 5i, M : 1 < Re z < 3;

1.16. w = 5iz+3+2i, M : 0 < Re z < 3; Im z > 0;

1.17. w = ( 1 i) + 2 iz,

;

M :

< arg z <

1.18. w = 3iz + 5 6i,

M : < arg z <

;

1.19. w = (2 2i)z 3 + 5i,

;

M :

< arg z <

1.20. w = 4iz + 3 5i,

M : 1 < Im z < 2;

1.21. w = (1 + i)z 2 + 4i,

M : jzj < 3; Im z > 0;

1.22.w = iz + 3 2i, M : jz 1 ij < 2; Re z > 0;

1.23.w = 3iz 2 + i, M : jzj < 1; 0 < arg z < 2 ;

1.24. w = (5 4i)z 6 2i, M : 1 < jz 2 + 3ij < 2;

1.25.w = 5iz + 1 + 3i, M : jzj < 3; 1 < Re z < 1;

1.26.w = 5iz + 1 3i, M : 2 < Re z < 2; 2 < Im z < 2;

148

1.27.w = 3iz 5 + 2i, M : 1 < Re z < 2; 1 < Im z < 4;

1.28.w = (1+i)z 2+4i, M : z = x+iy; x 2 < y < x+2;

1.29.w = ( 1 + i)z + 5, M : 0 < Re z < 2; 0 < Im z < 2;

1.30.w = 3z + 1 + 5i, M : 2 < Re z < 4; 0 < Im z < 5.

2.Найти линейное преобразование, переводящее точки z1, z2 в точки w1, w2 соответственно.

2.1. z1 = 2		+ i, z2 = 3i;	w1 = 4, w2 = 2 5i;
2.2. z1 = 1 + 2i, z2 = 3			i; w1 = 3 + 5i, w2 = 2i;
2.3. z1	= 0, z2 = 1 + i;		w1 = 3 2i, w2 = 7 + 2i;
2.4. z1	= 5	+ 2i, z2 = 1 + 4i; w1 = 1 3i, w2 = 8;
2.5. z1	= 6	+ i, z2 = 4i; w1 = 0, w2 = 2 i;
2.6. z1	= 3	+ 4i, z2 = 3	2i; w1 = 2i, w2 = 2 + 2i;

2.7.z1 = 1, z2 = 0; w1 = 6 + 5i, w2 = 3 5i;

2.8.z1 = 5 + i, z2 = 4; w1 = 1 + 4i, w2 = 3;

2.9. z1 = 2 + 5i, z2 = 1 + 3i;					w1 = 1 + i, w2 = 2i;
2.10. z1	= 4 2i,	z2	= i;	w1 = 3 + i, w2 = 1 + 8i;
2.11. z1	= 7 2i, z2 = 1			+ i;	w1 = 3 2i, w2 =	1;
2.12. z1	= 3 + 5i,	z2	= 2	+ 4i;	w1 = 1, w2 = 6	+ i;

2.13.z1 = 0, z2 = 3i; w1 = 2 + i, w2 = 1 + 2i;

2.14.z1 = 3 + 2i, z2 = 2; w1 = 5 3i, w2 = 4 + 3i;

2.15.z1 = 2 + i, z2 = 0; w1 = 0, w2 = 5 + 6i.

Найти линейное преобразование, оставляющее точку z0 неподвижной и переводящее точку z1 в точку w1.

2.16.z0 = 3, z1 = 2 + i, w1 = 1 3i;

2.17.z0 = 2 i, z1 = 3 + 4i, w1 = 2 i;

2.18.z0 = 4 + i, z1 = 1 + i, w1 = 2i;

2.19.z0 = 2 + 3i, z1 = 0, w1 = 3 + 2i;

2.20.z0 = 3 + i, z1 = 1 + i, w1 = 2i;

2.21.z0 = 5 + 3i, z1 = 2 + 4i, w1 = 1 6i;

2.22.z0 = 3, z1 = 2 + 5i, w1 = 1 2i;

2.23.z0 = 1 + 3i, z1 = 5 i, w1 = 3 + 2i;

2.24.z0 = 3 4i, z1 = 8 + 2i, w1 = 3 6i;

149

2.25.z0 = 4 5i, z1 = 4 + i, w1 = 6 + 3i;

2.26.z0 = 5 2i, z1 = 3 i, w1 = 2 + 3i;

2.27.z0 = 7 2i, z1 = 5 + 4i, w1 = 8i;

2.28.z0 = 3, z1 = 0, w1 = 4 + 2i;

2.29.z0 = 6i, z1 = 2 + 4i, w1 = 8 3i;

2.30.z0 = 1 + i, z1 = 1 + 3i, w1 = 2 + i.

3.Найти дробно-линейное отображение, переводящее точки z1; z2; z3 в точки w1; w2; w3 соответственно.

3.1. z1 = 1+i, z2 = 2+3i, z3 = 4 i;			w1 = 1 i, w2 = 5+2i,
w3 = 1 + 2i;			w1 = 1 + 2i, w2 = 1,
3.2. z1 = 0, z2 = 3 4i, z3 = 5 + i;
w3	= 2 3i;	= 1, z3 = 3 + i; w1	= 2 + 6i, w2 = 4 + 3i,
3.3. z1 = 0, z2
w3	= 5 i;
3.4. z1 = 1 + 4i, z2 = 3 + i, z3 = 5 i;			w1 = 7 + 2i, w2 = 4 + 5i,
w3	= 1;	z2 = 3 + 4i, z3 = 1 5i; w1 = 4 + 2i, w2 = 1,
3.5. z1 = 3 5i,
w3	= i;

3.6.z1 = 5i, z2 = 0, z3 = 8+4i; w1 = 3, w2 = 2 i, w3 = 3+4i;

3.7.z1 = 1 + 5i, z2 = i, z3 = 1; w1 = 0, w2 = 1, w3 = 2 + 3i;

3.8. z1 = 1 + i, z2 = 2 6i, z3 = 3 4i;		w1 = 5 + i, w2 = 4 3i,
w3	= 3 7i;			= 7 i,
3.9. z1 = 4 + 3i, z2 = 1 7i, z3 = 3i;		w1	= 2 + 4i, w2	= 7 i,
w3	= 1;			= 2 i,
3.10. z1 = 1, z2 = 4 + 2i, z3 = 2 + 3i;		w1	= 1 + 5i, w2	= 2 i,
w3	= 3 2i;

3.11. z1 = 4 + 3i, z2 = 1 + 3i, z3 = 1 5i; w1		= 3 5i,
w2 = 1 + 2i, w3 = 4;	w1 = 7 3i, w2 = 1,
3.12. z1 = 2 5i, z2 = 1 + 2i, z3 = 6 + 3i;	w1 = 7 3i, w2 = 1,
w3 = 4 5i;		= 4 2i,
3.13. z1 = 3 + 2i, z2 = 8, z3 = 1;	w1 = 0, w2	= 4 2i,
w3 = 5 3i;

150

3.14. z1 = 2 + 6i, z2 = 1 + 5i, z3	= 7 2i; w1 = 6 + i,
w2 = 2 i, w3 = 3 + 4i;
3.15. z1 = 1, z2 = 4 + i, z3 = 1 i;	w1 = 2 + 3i, w2 = 1 + 6i,
w3 = 2 + 4i;

3.16. z1 = 1 + i, z2 = 4 + 5i, z3 = 2 + i; w1 = 0, w2 = 3 2i, w3 = 4 + 3i;

3.17. z1 = 5 2i, z2 = 6 + 2i, z3 = 4 + i; w1 = 3 2i, w2 = 0, w3 = 3 + i;

3.18. z1 = 4 + i, z2 = 2 i, z3 = 3 + 4i; w1 = 1, w2 = 7 + i, w3 = 1 + 4i;

3.19. z1 = 2 + 3i, z2 = 1, z3 = 4 3i;	w1 = 1 i, w2 = 3 + 2i,
w3 = 6 + 5i;		w1 = 3 4i, w2 = 7i,
3.20. z1 = 2 + 7i, z2 = 0, z3 = 4 5i;
w3 = 3 + 2i;	= 5 3i;
3.21. z1 = 5 + 2i, z2 = 4 + 2i,z3			w1 = 3 + 4i,
w2 = 2 4i, w3 = 1;	w1 = 4 + 2i, w2 = 2 + 3i,
3.22. z1 = 0, z2 = 1 + 2i, z3 = 3 i;
w3 = 8i;			w2 = 4 + 5i,
3.23. z1 = 1, z2 = 2 5i, z3 = 3 + 5i;		w1 = i,
w3 = 1 + 7i;	w1 = 1 i, w2 = 3 i,
3.24. z1 = 4 3i, z2 = 0, z3 = 9 2i;
w3 = 4 + 5i;	w1 = 3 + 7i, w2 = 4 + 3i,
3.25. z1 = 0, z2 = 4 i, z3 = 2 + 5i;
w3 = 7i;		w1 = 1+4i, w2 = 3 5i,
3.26. z1 = 2 4i, z2 = 3+3i, z3 = 6 5i;
w3 = 2 4i;		w1 = 5 4i, w2 = 1,
3.27. z1 = 3 + i, z2 = 2 + 7i, z3 = 0;
w3 = 2 3i;	w1 = 1+5i, w2 = 3+4i,
3.28. z1 = 1, z2 = 3+5i, z3 = 2+4i;
w3 = 1 2i;
3.29. z1 = 1 i, z2 = 3i, z3 = 4 i;		w1 = 3, w2 = 1 + i,

w3 = 5 4i;

3.30. z1 = 2i, z2 = 2 + 3i, z3 = 0; w1 = 1, w2 = 4i, w3 = 5i.

151

4.Найти образ множества M при отображении w = z1.

4.1.M : z = x + iy; y = x + 4;

4.2.M : z = x + iy; y = 2x 3;

4.3.M : z = x + iy; y = 12x + 4;

4.4.M : z = x + iy; y = x + 5;

4.5.M : z = x + iy; y = 2x 4;

4.6.M : z = x + iy; y = x 3;

4.7.M : z = x + iy; y = 2x + 2;

4.8.M : z = x + iy; y = 3x 6;

4.9.M : z = x + iy; y = x + 4;

4.10.M : z = x + iy; y = 12x + 6;

4.11.M : jz 1 + ij = 1;

4.12.M : jz + 3 ij = 1;

4.13.M : jz 2 + 3ij = 2;

4.14.M : jz 1 ij = 3;

4.15.M : jz 1 + 2ij = 1;

4.16.M : jz 3 + 4ij = 2;

4.17.M : jz 2 + 2ij = 1;

4.18.M : jz 4 2ij = 3;

4.19.M : jz 1 + ij = 2;

4.20.M : jz 4 + 5ij = 2;

4.21.M : jz 3j = 3;

4.22.M : jz + 2ij = 2; p

4.23. M : jz 1 + ij = 2; p

4.24. M : jz + 2 3ij =p 13;


4.25. M : jz 2 + ij =		5;
4.26. M : jz 4	3ij =p5;
4.27. M : jz 1	ij =	2;
4.28. M : jz 5ij = 5;			p
4.29. M : jz + 2	+ 2ij = 2 2;
4.30. M : jz 1	+ 4ij =	p
		17:

5. Найти образ множества M при отображении w, разложив его на элементарные преобразования. Указать геометрический

смысл каждого преобразования.

5.1.

w =

(4 + 2i)z 7 + 5i

M :

= 1

;

z 2 + i

5.2.

w =

(3 4i)z + 6 + i

M :

2 + i = 2

z +

1 + i

;

5.3.

w =

(1 + 2i)z 9 + 2i

M :

3 + i

= 1

;

3 + 4i

152

5.4.

w =

(1 2i)z + 14 + 3i

M :

1 + 5i

= 1

;

z + 2 + 5i

5.5.

w =

(2 + 5i)z 16 3i

M :

= 3

;

z 1 + 3i

5.6.

w =

( 1 + 3i)z + 2 + 11i

M :

= 4

;

z + 4 i

5.7.

w =

(4 2i)z + 13 + 7i

M :

1 + 2i

= 3

;

z + 3 + 2i

5.8.

w =

( 2 + 2i)z + 1 5i

M :

i = 2

z 2 + 3i

;

5.9.

w =

(1 + 5i)z 15 + i

M :

1 + i

= 1

;

z 1 + 4i

w =

(3 i)z + 9 + 2i

M :

1 + i

= 3

5.10.

z + 3 + i

;

5.11.

w =

(1 + 2i)z 3 5i

M : z = x + iy; y = 2x

;

z + 4 i

5.12.

w =

( 1 3i)z + 5 4i

M : z = x + iy; y =

x + 2

;

z 2 + i

w =

(3 + 2i)z 1 i

M : z = x + iy; y = 3x

5.13.

z + 3 + 4i

;

5.14. w =

(2 + 4i)z 3 + 5i

M : z = x + iy; y = x + 3;

z 1 + i

5.15.

w =

(5 + 3i)z + 1 2i

M : z = x + iy; y =

2x + 1

;

z + 4 i

5.16.

w =

( 1 + 2i)z + 3 2i

M : z = x + iy; y = 2x

;

z 2 + 3i

5.17. w =

(3 4i)z 1 3i

M : z = x + iy; y = x + 2;

z + 5 i

5.18.

w =

(1 + 5i)z 4 3i

M : z = x + iy; y = x

;

z + 2 + 3i

5.19.

w =

(4 i)z + 1 i

M : z = x + iy; y =

x + 2

;

z 3i

5.20. w =

( 2 2i)z + 3 5i

, M : z = x + iy; y = 3x + 1;

z + 4 3i

5.21.

w =

(2 + 3i)z 1 4i

M : z = x + iy; y = x

;

4 + 2i

153

w =

( 3 + i)z 2 + 2i

M : z = x + iy; y =

5.22.

z + 3 2i

;

w =

(1 5i)z + 3 4i

M : z = x + iy; y = 2x

5.23.

z 2 + i

;

5.24.

w =

(2 + i)z + 5 2i

M : z = x + iy; y =

x + 1

;

z 4 + 3i

5.25.

w =

( 4 5i)z + 2 + 3i

M : z = x + iy; y = 3x

;

z 1 2i

5.26.

w =

( 1 + 2i)z 5 6i

M :

3 + 2i

= 2

;

z 3 + 4i

5.27.

w =

(2 + i)z 5 + 2i

M :

z + 2 + 3i

= 3

;

z 1 + 3i

w =

(1 + 3i)z 1 + 9i

M :

z + 1 + i

= 1

5.28.

z + 2 + i

;

5.29.

w =

(3 2i)z 7 i

M :

z + 1

= 2

;

z 1 i

5.30.

w =

(2 + 2i)z 6 + i

M :

1 + i

= 1

2 + i

6. Найти дробно-линейное отображение, отображающее область M на единичный круг так, чтобы точка z0 перешла в

центр круга.
6.1. M : Im z > 4;	z0 = 5i;
6.2. M : Im z > 5;	z0 = 2 + 6i;
6.3. M : Im z > 3;		z0 = 4i;
6.4. M : Im z > 2;	z0 = 3 + 3i;
6.5. M : Im z > 3;	z0 = 5i;
6.6. M : Im z > 2;		z0 = 2 + 3i;
6.7. M : Im z > 1;		z0 = 4 + i;
6.8. M : Re z < 1;	z0 = 2 + i;
6.9. M : Re z > 0;	z0 = 5 3i;
6.10. M : Re z > 3;		z0 = 4 i;
6.11. M : Re z > 2;		z0 = 2i;
6.12. M : Re z > 5;		z0 = 6 + 3i;
6.13. M : Re z > 4;		z0 = 1 + 2i;

154

6.14. M : Re z > 2;

z0 = 3 4i;

6.15. M : Re z > 1;

z0 = 1 + 3i;

6.16. M : jz 2 ij < 3;

z0 = 1 + i;

6.17. M : jz + 2 + 3ij < 2;

z0 = 1 2i;

6.18. M : jz 3 + ij < 2;

z0 = 2 + 2i;

6.19. M : jz + 1 + ij < 3;

z0 = 1 i;

6.20. M : jz 2 3ij < 3;

z0 = 1 + 2i;

6.21. M : jz 4ij < 2; z0 = 1 + 3i;

6.22. M : jz 3 2ij < 4;

z0 = 3 + i;

6.23. M : jz 1 ij < 3;

z0 = 1 i;

6.24. M : jz + 3 + 2ij < 2;

z0 = 2 i;

6.25. M : jz + 1 4ij < 3;

z0 = 1 + 2i;

6.26. M : jz + 2 ij < 4;

z0 = 1 + 3i;

6.27. M : jz 4 + 3ij < 5;

z0 = 2 3i;

6.28. M : jz + 3 + ij < 2;

z0 = 2 2i;

6.29. M : jz + 1 + 2ij < 2;

z0 = 3i;

6.30. M : jz 3 4ij < 3;

z0 = 1 + 5i.

7. Найти образ области M при отображении w.

7.1. w = z2;

M : jzj < 3;

0 < arg z < ;

7.2. w = z4;

M : jzj < 2;

0 < arg z <

;

7.3. w = z5;

M : jzj < 1;

< arg z <

;

7.4. w = z3;

M : jzj < 4;

0 < arg z <

;

7.5. w = z2;

M : jzj > 1;

< arg z < ;

7.6. w = z4;

M : jzj > 2;

Re z > 0; Im z > 0;

7.7. w = z3;

M : jzj < 1;

< arg z <

;

M : jzj < 2;

Re z

< 0; Im z > 0

;

7.8. w = z

7.9. w = z3; M : 1 < jzj < 2;

< arg z < ;

155

7.10. w = z4;

M : jzj > 3;

0 < arg z <

;

7.11. w = z3;

M : 2 < jzj < 4;

0 < arg z <

;

7.12. w = z4;

M : jzj < 2;

< arg z <

;

7.13. w = z5;

M : jzj > 1;

0 < arg z <

;

7.14. w = z6;

M : jzj > 2;

0 < arg z <

;

7.15. w = z2;

M : jzj < 3;

< arg z <

;

7.16. w = z2;

M : Im z > 0;

Im z > 0;

7.17. w = z3;

M : Re z > 0;

7.18. w = z4;

M : Re z > 0;

Im z > 0;

7.19.w = z3; M : 0 < arg z < 4 ;

7.20.w = z2; M : 4 < arg z < 34 ;

7.21.w = z3; M : 0 < arg z < 6 ;

7.22.w = z4; M : 4 < arg z < 2 ;

7.23.w = z2; M : 6 < arg z < 3 ;

7.24. w = z4;

M : jzj > 2;

0 < arg z <

;

7.25. w = z5;

M : jzj > 1;

0 < arg z <

;

7.26. w = z4;

M : jzj < 2;

< arg z <

;

7.27. w = z3;

M : 2 < jzj

< 3;

0 < arg z <

;

7.28. w = z2;

M : 2 < jzj

< 4;

0 < arg z <

;

156

7.29. w = z3;

M : 2 < jzj < 3;

0 < arg z <

;

7.30. w = z4;

M : jzj > 3;

0 < arg z <

множество

Найти

отображение,

переводящее

M : 0 < Re(inz) < a, где n

номер варианта,

коли-

чество букв в вашей фамилии, на единичный круг.

Найти

отображение,

переводящее

множество

M :

< arg z <

, где n

номер варианта,

множе-

a количество букв

в вашей

ство

N : 0 < Re w < a, где

фамилии, на полосу 0 < Re z < 1:

10. Найти отображение, переводящее область D на верхнюю полуплоскость, если область D задана системой нера-

венств.		+ 2ij > 2;
10.1. jz 2 + 3ij < 3; jz 2
10.2. jz 1 4ij < 2; jz 1		3ij > 1;
10.3. jz + 1	2ij < 3; jz 1	2ij > 1;
10.4. jz 2	+ ij < 2; jz 3 + ij > 1;
10.5. jz 1	p		p
	+ ij < 2; jz 1 ij < 2;

10.6.jz 1j < 1; jz ij < 1;

10.7.jz + 2j < 2; jz 2ij > 2;

10.8. jz 1j < 1;pjz + ij > 1; p

10.9. jz 2ij < 2 2; jz + 2ij > 2 2; p

10.10. jz + ij > 2; jzj < 1;

10.11.jz 2 2ij > 2; Re z > 0;

10.12.jz 1 + 3ij > 3; Re z > 2;

10.13.jz + 3 2ij > 1; Re z > 3;

10.14.jz 3 + ij > 2; Re z > 1;

10.15.jz 2 + ij > 3; Re z > 1;

10.16.jz 4 2ij < 4; Re z > 0;

10.17.jz + 1 + 3ij < 2; Re z < 1;

10.18.jz + 2 ij < 3; Re z < 1;

10.19.jz 3 + ij < 1; Re z > 3;

10.20.jz 1 + 2ij < 4; Re z < 1;

157

10.21.jz 1 + 2ij < 3; Im z > 2;

10.22.jz 3 ij > 1; Im z > 1;

10.23.jz + 2 3ij > 2; Im z < 5;

10.24.jz + 1 2ij < 4; Im z < 2;

10.25.jz 4 + ij < 3; Im z > 1;

10.26.jz + 2 ij > 4; Im z > 3;

10.27.jz + 1 2ij > 1; Im z < 3;

10.28.jz 4 + 2ij > 2; Im z < 0;

10.29.jz 5 3ij < 5; Im z < 3;

10.30.jz + 2 + ij > 2; Im z > 1.

11.Представить комплексное число ab в алгебраической

форме.

11.16. a = 1 + p

11.1. a = 2 +

2i, b = 3 + i;

i, b = 2 + i;

11.2. a = p

+ i, b = 1 2i;

11.17. a = 1 + i, b = 8i;

11.3. a = 5 + 5i, b = 2 3i;

11.18. a = 4 4p

i, b = 5 + 2i;

11.4. a = 2

11.19. a = 3 3i, b = 1 + 7i;

2 3i, b = 1 + i;

11.5. a = 3

3i, b = 5i;

11.20. a = i, b = 8 + 2i;

11.6. a = 1

3i, b = 7 + 2i;

11.21. a = 2 3 2i, b = 4 7i;

11.7. a = 2i, b = 4 + 3i;

11.22. a = 5 5i, b = 3 + 6i;

11.8. a = p

+ i, b = 4 3i;

11.23. a = 1+p

3i, b = 7+2i;

11.9. a = 3 i, b = 3 + 5i;

11.24. a = 4 4 3i, b = 3 + 2i;

11.10.a = 2 2i, b = 8 + 3i; 11.25. a = 2 + 2i, b = 4 i;

11.11.a = 7 + 7i, b = 1 5i; 11.26. a = 8 8i, b = 3 + 5i; p p

11.12. a = 3		3 3, b = 4 + i;	11.27. a = 7 + 7		3i, b = 2 4i;
11.13. a = 3i, b = 1 2i;			11.28. a = 2 + 2i, b = 4 i;
p		p	p
11.14. a =	6+ 2 , b = 3+3i;		11.29. a = 2	3 + 2i, b = 3i;

11.15.a = 4 4i, b = 2 + 5i; 11.30. a = 7 7i, b = 1 + 2i.

12.Решить уравнения sin z = a, cos z = b, tg z = c, ctg z = d.

12.1.a = 2, b = 3i, c = 2 3i, d = 1 + 2i;

12.2.a = 3, b = 2i, c = 4 i, d = 1 + 3i;

12.3.a = 5i, b = 4, c = 5 + 3i, d = 4 2i;

12.4.a = 2i, b = 5, c = 3 + i, d = 4 + 2i;

158

12.5.a = 3, b = 2i, c = 1 3i, d = 2 + i;

12.6.a = 7i, b = 4, c = 2 5i, d = 1 + 2i;

12.7.a = 4, b = 3i, c = 2 + 3i, d = 4 i;

12.8.a = 2i, b = 5, c = 3 + 5i, d = 1 + i;

12.9.a = 7i, b = 2, c = 2 2i, d = 7i;

12.10.a = 3, b = 5i, c = 1 + 3i, d = 3 4i;

12.11.a = i, b = 3, c = 2 + i, d = 3 4i;

12.12.a = 4, b = 2i, c = 3 2i, d = 1 + i;

12.13.a = 2, b = 4i, c = 3 + 5i, d = 7 i;

12.14.a = 8i, b = 2, c = 1 + i, d = 2 + 3i;

12.15.a = 3, b = 5i, c = 1 i, d = 2 + 4i;

12.16.a = 5i, b = 3, c = 1 + 2i, d = 3 5i;

12.17.a = 2i, b = 4, c = 3 i, d = 2 + 7i;

12.18.a = 3, b = i, c = 4 + 6i, d = 3i;

12.19.a = 2, b = i, c = 4 2i, d = 1 + i;

12.20.a = 2i, b = 3, c = 5 + 2i, d = 3 + 7i;

12.21.a = 3i, b = 4, c = 3 5i, d = 1 + 2i;

12.22.a = 4i, b = 3, c = 1 i, d = 2 7i;

12.23.a = 3i, b = 2, c = 5 i, d = 2 + i;

12.24.a = 3i, b = 2, c = 2 i, d =;

12.25.a = 5, b = 4i, c = 1 + 3i, d = 2 i;

12.26.a = 4, b = i, c = 2 i, d = 3 + 3i;

12.27.a = 5i, b = 2, c = 2 + 3i, d = 4 + 5i;

12.28.a = 2i, b = 5, c = 3 i, d = 2 + 6i;

12.29.a = 3i, b = 6, c = 1 4i, d = 2 5i;

12.30.a = 2, b = 3i, c = 3 4i, d = 1 + i.

Решение типового варианта

Пример 1. Найти образ множества M : jz 1j = 2 при отображении w = (2 + 2i)z + 1 3i, разложив его на элементарные преобразования. Указать геометрический смысл каждого преобразования.

159

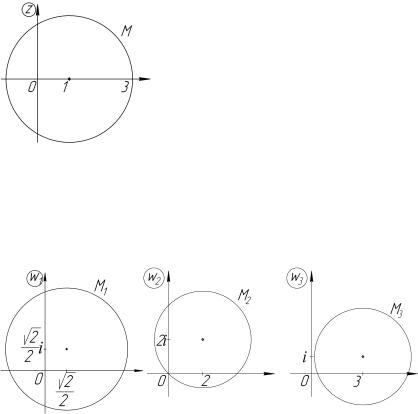
Решение. Множество M представляет собой круг с центром в точке c = 1 и радиусом 2 (рис. 4.23). Разложим отображение w на элементарные составляющие. Для этого представим число 2 + 2i

	в показательной форме. Очевидно,
	p	4 i	. Тогда отображение
	p	4 i
	2 + 2i = 2 2e
Рис. 4.23	w можно представить в виде компо-
Рис. 4.23	зиции следующих преобразований:
	w1 = e 4 iz поворот на угол			про-
	w1 = e 4 iz поворот на угол			про-
тив часовой стрелки;			4
тив часовой стрелки;
p			p

w2 = 2 2w1 подобие с коэффициентом 2 2;

w3 = w2 + 1 3i параллельный перенос на вектор 1 3i.

Рис. 4.24	Рис. 4.25	Рис. 4.26
Рис. 4.24

Найдем образы множества M при каждом из этих преобра-

зований. При повороте радиус круга не изменится, а центр сме-

стится в точку c1 = c e 4 i =

i: Таким образом, множе-

ство M1 примет вид: jw1

ij = 2 (рис. 4.24). При по-

добии радиус круга станет 4

, а центр c2 = 2

c1 = 2 + 2i;

160

то есть M2 : jw2 2 2ij = 4 2 (рис. 4.25). При параллельном переносе центр круга сместитсяpв точку c3 = c2 + 1 3i = 3 i: Итак, получили jw 3 + ij = 4 2 искомый образ (рис. 4.26).

Пример 2. Найти линейное преобразование, оставляющее точку z0 = 1 + 4i неподвижной и переводящее точку z1 = 1 i в точку z2 = 6 6i.

Решение. Искомое линейное преобразование имеет вид w = az + b, где a и b комплексные числа. Для нахождения коэффициентов a; b необходимо решить систему

(

a(1 + 4i) + b = 1 + 4i; a(1 i) + b = 6 6i:

Вычитая из первого уравнения второе и подставляя найденное выражение для a, например в первое уравнение, получим

a =	5 + 10i	= 2	i; b = 1 + 4i	(2	i) = 3 + 5i:
	5i

Таким образом, w = (2 i)z + 3 + 5i.

Пример 3. Найти дробно-линейное отображение, переводящее точки z1; z2; z3 в точки w1; w2; w3 соответственно:

а) z1 = 0; z2 = 1 + i; z3 = i; w1 = 4 + 2i; w2 = 1; w3 = 0; б) z1 = 1 + 2i; z2 = i; z3 = 4; w1 = 3; w2 = 1 2i; w3 = 3i.

Решение. Искомое дробно-линейное отображение имеет вид w = azcz ++ db, где a; b; c; d комплексные числа.

а) Коэффициенты a; b; c; d находим из условий

azk + b = wk; k = 1; 2; 3: czk + d

Получим систему

8 db = 4 + 2i;

c(1 + i) + d = 0;

> ai + b = 0:

161

Разрешив ее относительно a, b и c, найдем

a = (2 4i)d; b = (4 + 2i)d; c = (

i)d:

Следовательно,

w =

(2 4i)dz + (4 2i)d

(4 8i)z + 8 + 4i

( 1 + i)z + 2

(

i)dz + d

б) Воспользуемся ангармоническим соотношением трех то-

чек (4.7) и выразим w.

z 1 2i

4 1 2i

w 3

3i 3

;

z i

4 i

w 1 + 2i 3i 1 + 2i

z 1 2i

4 i

w 3

1 + 5i

;

3 2i

w 1 + 2i

z i

3 + 3i

(z i)(3 2i)(w 3)( 1 + 5i) =

= (z 1 2i)(w 1 + 2i)(4 i)( 3 + 3i);

(z i)(w 3)(7 + 17i) = (z 1 2i)(w 1 + 2i)( 9 + 15i);

w((z i)(7 + 17i) (z 1 2i)( 9 + 15i)) = = (z i)((21 + 51i) + (z 1 2i)( 21 33i));

w(z(16 + 2i) 22 10i) = 18zi + 6 + 54i;
			18iz + 6 + 54i
	w =								;
	w =	(16 + 2i)z 22 10i							;
			9iz + 3 + 27i
	w =							:
	w =		(8 + i)z 11 5i					:
Пример	4. Найти образ множества M : z = x + iy;
	1
y = 2x + 1	при отображении w =						.
y = 2x + 1	при отображении w =					z	.
Решение. I способ. Множество M представляет собой пря-
мую (рис. 4.27). Так как w =				1	, то можно записать z =					1	: Вы-
мую (рис. 4.27). Так как w =					, то можно записать z =						: Вы-
				z						w
	162

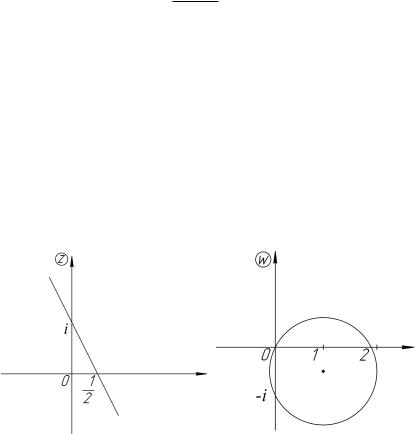
делим действительную и мнимую части последней функции, считая w = u + iv.

x + iy =	1	=	u iv	=	u	i	v	:
	u + iv		u2 + v2		u2 + v2		u2 + v2

Подставляя x = u=(u2 + v2) и y = v=(u2 + v2) в уравнение y = 2x + 1, найдем

+ 1; u2 + v2 2u + v = 0:

u2 + v2

Выделяя полные квадраты, представим последнее уравне-

ние в виде

(u 1)2 + v +

Таким образом,

прямая M

перейдет в окружность

N :

w 1 +

(рис. 4.28).

	Рис. 4.27				Рис. 4.28
	Рис. 4.27
II способ. Отображение w =				1	является композицией ин-
II способ. Отображение w =				z	является композицией ин-
		1		z
версии w1	=		и зеркального отображения w2 =				.
						w1
						w1
		z

163

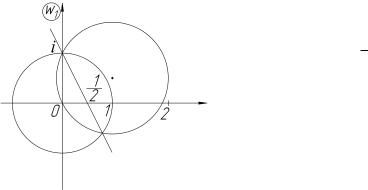
Найдем образы множества M при каждом из этих преобразований. Так как прямая M не проходит через начало координат, то образом ее при отображении w1 будет окружность. Так как при инверсии бесконечно удаленная точка перейдет в начало координат, то искомая окружность пройдет через 0. Значит, уравнение ее будет иметь вид

x2 + ax + y2 + by = 0; a 2 R; b 2 R:

Для нахождения коэффициентов a и b необходимо знать две точки окружности. Най-

дем: w1(i) = i, w1 2 = 2.

Таким образом, решив систему

(

4 + 2a = 0;

1 + b = 0;

получим

a = 2,

b = 1.

Следовательно,

уравнение

Рис. 4.29

окружности примет вид

+ y

(x 1)2

;

т.е.

(рис. 4.29).

1 2

При

отображении

w2 данная окружность отобразится зер-

2 :

кально относительно действительной оси:

w2 1 +

Итак, получили образ N : w

1 +

M :

z + 1

Пример 5. Найти образ

множества

= 3

при отображении w =

3z + 2i

, разложив его на элементар-

iz 1 + i

164

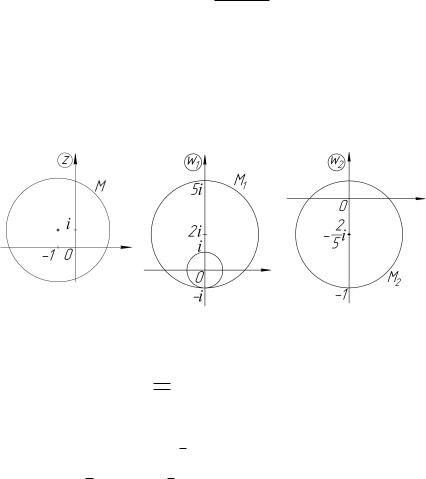
ные преобразования. Указать геометрический смысл каждого преобразования.

Решение. Разложим отображение w на элементарные преобразования. Для этого выделим целую часть

w = 3i + 1 + 3i : z + 1 + i

Множество M представляет собой окружность радиуса 3 с центром в точке c0 = 1 + i (рис. 4.30).

Отображение w1 = z + 1 + i задает параллельный перенос на вектор 1 + i. Множество M при этом отображении перейдет в окружность M1 : jw1 2ij = 3 радиуса 3 с центром в точке c1 = 2i (рис. 4.31).

Рис. 4.30	Рис. 4.31	Рис. 4.32
	Рис. 4.31

Отображение w2 = 1 инверсия. Окружность M1 не про- w1

ходит через начало координат, значит, ее образом при отображении w2 будет окружность M2. Точка i останется неподвиж-

ной, а точка 5i перейдет в 15i. Следовательно, диаметр окружности равен 65, а радиус 35. Таким образом, центр окружности

165

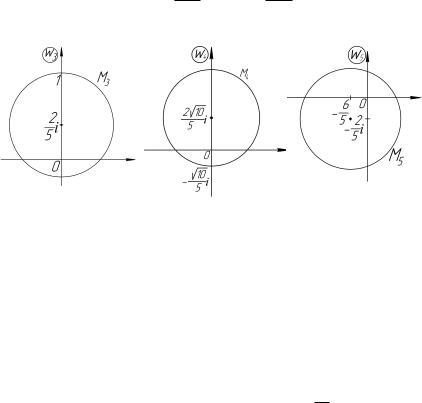
M2 находится в точке c2 =

i. В итоге получим множество

: w2

i =

(рис. 4.32).

Отображение

w3 =

(зеркальное отображение) переведет

множество M2 в M3 : w3 +

i =

(рис. 4.33).

Представим число 1 + 3i в показательной форме. Для это-

го

вычислим j

1 + 3ij =

. Следовательно, 1 + 3i =

10 e

, где

cos ' =

, sin ' =

, ' угол второй

четверти.

Рис. 4.33

Рис. 4.34

Рис. 4.35

Преобразование

(подобие

с коэффи-

циентом

)

переводит

окружность

M4,

радиуса

центром

точке c4

2 10

i, т.е.

: w

i =

(рис. 4.34).

w5 = e

осуществляет поворот на угол

Преобразование

' вокруг начала координат. Окружность M при этом отобра-

4 p

жении перейдет в окружность M5 радиуса	3 10	с центром в
	5

166

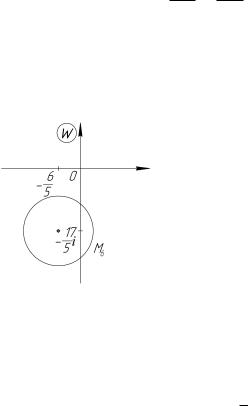
точке

c5 = c4 ei' =

i (cos ' + i sin ') =

i (

i) =

: w5 +

i =

т.е. M5

(рис. 4.35).

задает

параллель-

Преобразование

w = w6 = w5

ный перенос

на

вектор

3i. Окружность M5 при этом

перейдет в окружность M6 радиуса

c центром в точке

c6 =

i 3i =

В результате образом исходной

окружности

при

отображении

будет окружность M6

: w6 +

i =

(рис. 4.36).

Рис. 4.36

Пример 6. Отобразить область Re z > 1 в единичный круг так, чтобы точка z = 2 перешла в центр круга.

Решение. Отобразим сперва заданную область (рис. 4.37) на верхнюю полуплоскость. Для этого необходимо выполнить сдвиг влево на 1 и поворот на угол 2 ; т.е.

w1 = e 2 (z 1) = i(z 1):

Точка 2 при этом перейдет в точку w1(2) = i(2 1) = i (рис. 4.38). Отображение верхней полуплоскости на единичный круг (рис. 4.39) выполним по формуле (4:9). Таким образом,

167

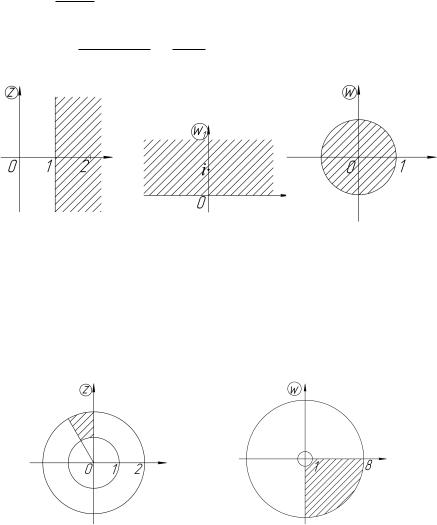
w2 = ei w1 i; где можно выбрать произвольно, так как до- w1 + i

полнительных условий не задано. Возьмем = 0: В итоге по-

лучим w =	i(z 1)	i	=	z 2	:
	i(z 1)	+ i		z

	Рис. 4.37		Рис. 4.38	Рис. 4.39
	Пример		7. Найти образ области	1 < jzj < 2;
	< arg z <	2	при отображении w = z3:
2
	3
	Решение. Так как степенная функция w = z3 увеличи-

вает аргумент в три раза, а модуль возводит в куб, то ис-

Рис. 4.40

Рис. 4.41

168

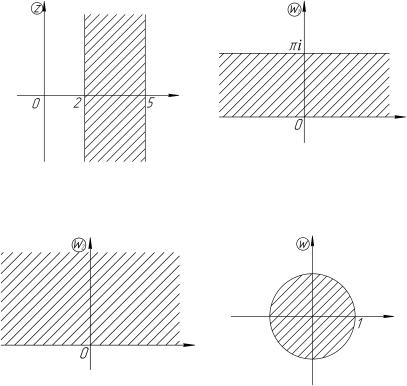
ходная область (рис. 4.40) отобразится в область 1 < jzj < 8,

3		< arg z < 2 (рис. 4.41).
	2
		Пример 8. Отобразить полосу 2 < Re z < 5 на единичный

круг.
		Решение. Показательная функция w = ez отобража-
ет		полосу 0 < Im z < на верхнюю полуплоскость. Значит,

Рис. 4.42	Рис. 4.43

Рис. 4.44

Рис. 4.45

вначале отобразим полосу 2 < Re z < 5 (рис. 4.42) на полосу

169

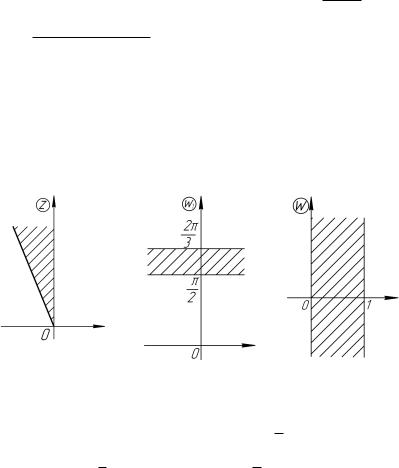
0 < Im z < (рис. 4.43). Для этого выполним сдвиг на 2 вле-

во, подобие с коэффициентом

и поворот на угол

, т.е.

1 + p

= ei

(z 2) =

w1 = i

(z 2): Тогда w2 = ew1

ez 2:

Верхняя полуплоскость (рис. 4.44) отобразится на единичный круг (рис. 4.45) с помощью дробно-линейного отображе-

ния (4:9), где возьмем = 0, а z0 = i, тогда w =

w2 i

, откуда

w2 + i

w = (1 + p

i)ez 2 2i:

1 + p

i)ez 2 + 2i

Пример 9. Отобразить

угол

< arg z <

на

полосу

0 < Re z < 1:

Решение. Функция w1 = ln z отображает указанный угол

(рис. 4.46) на полосу

< Im z <

шириной

(рис. 4.47).

6iw

Далее функция w = w1

e 2 i = =

+ 3 осу-

Рис. 4.46	Рис. 4.47	Рис. 4.48
	Рис. 4.47

ществляющая параллельный перенос на 2 вниз, подобие с коэффициентом 6 , и поворот на угол 2 переведет полученную

170

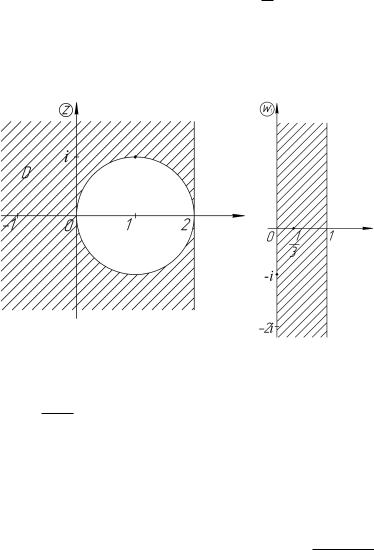
полосу на заданное множество 0 < Re z < 1 (рис. 4.48). Таким образом, окончательно получим w = 6i ln z + 3.

Пример 10. Отобразить область D : jz 1j > 1; Re z < 2, конформно на верхнюю полуплоскость.

Решение. Прямая Re z = 2 касается указанной окружности в точке z = 2 (рис. 4.49). Дробно-линейное отображение

Рис. 4.49

Рис. 4.50

w1 = z 2 переводит точку 2 в 1. Значит, в силу кругового

свойства дробно-линейной функции и окружность jz 1j = 1, и прямая Re z = 2 перейдут в две параллельные прямые.

Образом окружности будет прямая, проходящая через 0. Для того чтобы уточнить положение этой прямой, достаточно найти образ еще одой точки окружности.

(1 + i) =

1 + i

(1 + i)2

1 + 2i 1

1 + i

171

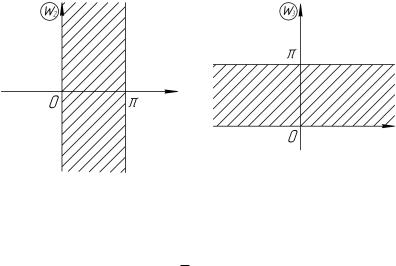
Значит, образом окружности будет мнимая ось. Чтобы определить положение образа прямой Re z = 2 в плоскости w1,

достаточно знать одну точку.
w1(2 + i) =	2 + i	=	2 + i	= i(2 + i) = 1 2i:

	2 + i 2		i

Следовательно, образом будет прямая Re w1 = 1. Найденные две параллельные прямые разбивают плоскость w1 на три

части. Так	как	образом точки z = 1 является			1		,
					w1 =
						3
то область	D отобразится		в полосу	0 < Re w1	< 1 (рис.
4.50). Функция		w2 = w1	отобразит	эту полосу	на полосу

Рис. 4.51	Рис. 4.52

0 < Re w2 < (рис. 4.51), а функция w3 = e 2 iw2 = iw2 повернет последнюю на угол 2 . В результате получим полосу

0 < Im w3 < (рис. 4.52), которая отобразится на верхнюю полуплоскость отображением w4 = ew3 . Составив композицию указанных выше отображений, получим:

w = ez 2 :

172

Пример 11. Представить комплексное число (1 + i)2+i в алгебраической форме.

Решение. Воспользуемся формулой (4.18).

(1 + i)2+i = e(2+i)Ln(1+i) = e(2+i)(ln j1+ij+iArg(1+i)) =

p p p

= e(2+i)(ln 2+i( 4 +2 k)) = e2 ln 2 4 2 k+i(ln 2+ 2 +4 k) =

= eln 2

2 k cos ln 2 +

+ 4 k + i sin ln 2 +

+ 4 k =

2 cos(ln 2 +

+ 4 k)

2 sin(ln 2 +

+ 4 k)

+ i

;

e 4 2 k

где k 2 Z:

Пример 12. Решить уравнения a) sin z = 2i, б) cos 2z = 9, в) tg z = 4 + i, г) ctg z = 7i:

Решение. а) Очевидно z = Arcsin( 2i): Представим это число в алгебраической форме. По формуле (4.25) найдем

Arcsin( 2i) = i Ln i ( 2i) p

= i Ln(2 p

1 ( 2i)2

5):

Далее воспользуемся формулой (4.17):

Ln(2 + 5)=ln j2 +

5j+ i(arg(2 + 5) + 2 k)=ln(2 + 5) + 2 ki;

Ln(2

5) = ln j2 5j + i(arg(2

5) + 2 k) =

= ln( 5 2) + i( + 2 k) = ln(

5 2) + i (2k + 1):

В итоге получим

z = 2 k i ln(2 +

5) и z = (2k + 1) i ln(

5 2):

б) По формуле (4.24) найдем

Ln(9 + p92

12) =

p80) =

z =

Arccos 9 =

Ln(9

173

=2i (ln j9 p80j + i(arg(9 p80) + 2 k)) =

=2i (ln(9 p80) + i2 k) = k 2i ln(9 p80);

где k 2 Z:

в) По формуле (4.26) найдем

z = Arctg(

4 + i) =

1 + i( 4 + i)

4 + i) 2i

1 + 2i

= 2i Ln

2i)

= 2i Ln

2i(1

= 2i ln

+ i arg

+ 2 k ;

где k

2 Z

: Найдем

p42 + 22 =

;

arg	4	2	i	= '; cos ' =	2	5	;	sin ' =	5	:

	5	5				5			5
				p

Таким образом, ' = + arcsin												5		: Окончательно получим

					2p						5						p				+ 2 k!! =

1						5													5
z =				ln			+ i				+ arcsin
	2i				5													5
														p									2p
				(2k + 1) 1												5				i					5
=								+			arcsin										ln					;
				2						2					5					2				5
где k 2 Z:
г) Используя (4.27), получим
z =		1	Arcctg 7i =						1		Ln		i 7i 1						=			1		Ln			4	=
									6i
3												i 7i + 1 6i														3

	1		4		k	i		4
=		ln		+ 2 ki =			ln		;
	6i		3		3	6		3

где k 2 Z:

174

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1714 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.02.201627.65 Кб96ТТХ БМП-2.doc
#
18.02.201626.62 Кб231ТТХ ПЗРК Игла.doc
#
18.02.201610.64 Mб50Туник, Креативные тесты.doc
#
14.04.2019246.27 Кб2Туроперейтинг.doc
#
11.09.201929.06 Кб2ТУРОПЕРЕЙТИНГ.docx
#
18.02.201618.41 Mб252ТФКП Детченя, Кулеш, Пецевич, Романовский.pdf
#
18.02.201669.12 Кб47Тэма.doc
#
18.02.201631.71 Кб5Тэматыка практычных заняткаў.docx
#
18.02.2016108.28 Кб10тэн.docx
#
20.12.201861.65 Кб62Тэорыя.docx
#
25.09.20191.58 Mб25ТЭЦ для чтения.docx