Решение. Воспользуемся формулой (4.18).

(1 + i)2i = e2i Ln(1+i) = e2i(ln j1+ij+i Arg(1+i)) =

p

= e2i(ln 2+i( 4 +2 k)) = e 2 4 k+i ln 2 =

= e 2 4 k cos ln 2 + ie 2 4 k sin ln 2;

где k 2 Z:

4.7. Функция Жуковского

Функцией Жуковского называется функция вида

С помощью этой функции Жуковский нашел идеальную форму для крыла самолета, чтобы уменьшить турбулентные движения воздуха.

Функция (4.20) является аналитической на всей комплексной плоскости, за исключением точки z = 0. Вычисляя производную функции (4.20), получаем:

Отсюда следует, что производная функции Жуковского отлична от нуля во всех точках плоскости z, кроме точек 1: Тем самым отображение, осуществляемое этой функцией, является конформным в окрестности любой точки z, за исключением этих двух точек.

Найдем области однолистности функции Жуковского. Предположим, что две различные точки комплексной плоскости z1 6= z2 переводятся функцией (4.20) в одну и ту же точку плоскости w, т.е.

131

или

z1 z2 = z1 z2 : z1 z2

Так как z1 6= z2, то из последнего соотношения следует z1 z2 = 1. Полученное условие означает, что областями однолистности функции Жуковского будут такие области, которые не могут содержать подобных точек. В частности, единичный круг jzj < 1 и область jzj > 1. Обе эти области конформно отображаются функцией (4.20) на одну и ту же область плоскости w. Чтобы определить эту область, рассмотрим отображение окружностей jzj = r0, осуществляемое функцией (4.20). Для этого перейдем к показательной форме записи комплексных чисел z = rei' и выделим действительную и мнимую части функции (4.20):

Из соотношения (4.21) следует, что функция (4.20) отображает концентрические окружности jzj = r0 в эллипсы, при этом фокусы всех этих эллипсов лежат в точках c = 1 действительной оси u. Следовательно, функция (4.20) производит отображение семейства концентрических окружностей jzj = r0 плоскости z на семейство софокусных эллипсов плоскости w. При этом, если r1 < 1, то положительному направлению обхода окружности jzj = r1 соответствует отрицательное направление обхода

эллипса (4.21), если r2 = 1 > 1, то положительному направле- r1

нию обхода окружности jzj = r2 положительное направление

132

обхода эллипса (4.21). При r1 ! 1 эллипс (4.21) вырождается в отрезок [ 1; 1] действительной оси u, проходимый дважды. При r1 ! 0 эллипс (4.21) переходит в окружность бесконечно большого радиуса.

Значит, функция Жуковского производит конформное отображение области внутри единичного круга jzj < 1 комплексной плоскости z на плоскость w с разрезом по отрезку [ 1; 1] действительной оси. Граница области окружность jzj = 1 отображается на этот отрезок, при этом верхняя полуокружность отображается на нижний, а нижняя на верхний берег разреза. Аналогично, внешность круга jzj > 1 плоскости z отображается на второй экземпляр плоскости w, разрезанный по отрезку [ 1; 1] действительной оси, причем верхняя полуокружность jzj = 1, Im z > 0, отображается на верхний берег, а нижняя полуокружность jzj = 1, Im z < 0 на нижний берег разреза. Тем самым, функция Жуковского (4.20) осуществляет конформное отображение полной плоскости z на риманову поверхность обратной функции

p

z = w + w2 1: (4.22)

Риманова поверхность функции (4.22) представляет собой двулистную поверхность, составленную из двух экземпляров плоскости w, разрезанной вдоль отрезка [ 1; 1] действительной оси. Точки w = 1 являются точками ветвления функции (4.22).

Следует также отметить, что функция Жуковского (4.20) отображает отрезки лучей arg z = '0 в семейство софокусных гипербол:

причем фокусы этих гипербол лежат в точках c = 1 действительной оси u.(Проверку последнего утверждения предлагается выполнить читателю).

133

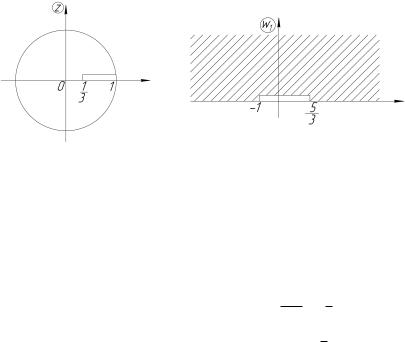
Пример 4.7. Отобразить круг jzj < 1 с разрезом по отрез-

Длина этого отрезка равна 8=3, а центр его находится в точке

w1 = 1=3. Отобразим полученную область на всю плоскость с разрезом по отрезку [ 1; 1] (рис. 4.17). Для этого нужно центр

образование подобия с тем, чтобы длина отрезка стала равной 2

(следовательно, коэффициент подобия равен 82=3 = 34). Таким

образом, плоскость w1 с разрезом по отрезку 1; 53 отобра-

134

жается на плоскость w2 с разрезом по отрезку [ 1; 1] функцией

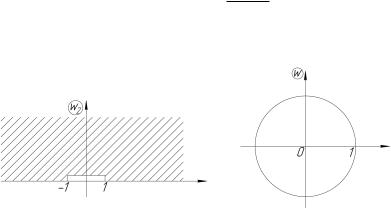
а эта последняя область отображается, как мы знаем, на внутренность единичного круга (рис. 4.18) функцией, обратной по отношению к функции Жуковского,

q

w = w2 + w22 1

(точнее, одной из ветвей этой функции).

Рис. 4.17

Рис. 4.18

135