1. Теорема Ролля

Теорема 1.1. Если функция непрерывна на отрезке, дифференцируема во всех его внутренних точках, а на концах отрезка,обращается в ноль, то существует, по крайней мере, одна точка, в которой.

Следует отметить, что данная теорема справедлива и в том случае, когда на концах отрезка функция не обращается в ноль, но принимает равные значения.

Геометрический смысл данной теоремы следующий: если непрерывная кривая пересекает ось в двух точках,или принимает в них равные значения, то, по крайней мере, в одной точке междуикасательная к кривой параллельна оси.

Необходимо отметить, что если не во всех точках у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции  (риДанная функция непрерывна на отрезкеи обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.

2. Теорема Лагранжа

Теорема. Если функция непрерывна на отрезкеи дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка, в которой.

Согласно теореме Ролля в точке производная, то естьи,

что и требовалось доказать.

Геометрический смысл теоремы Лагранжа следующий: внутри отрезка существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, притеорема переходит в теорему Ролля.

3. Теорема Коши

Теорема. Если функции инепрерывны на отрезкеи дифференцируемы во всех его внутренних точках, причемне обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка, в которой.

Данная функция непрерывна на отрезке и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точкахидает:. Значит, функцияудовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка, в которой.

В случае, когда , теорема Коши переходит в формулировку теоремы Лагранжа.

4. Правило Лопиталя

Теорема. Пусть функции инепрерывны и дифференцируемы во всех точках полуинтервалаи присовместно стремятся к нулю или бесконечности. Тогда, если отношение их производных имеет предел при, то этот же предел имеет отношение и самих функций, то есть.

50ВОПРОСФормула Тейлора и различные формы её остаточного члена. Основные разложения элементарных функций по формуле Тейлора.

Теорема:

Пусть функция имеетпроизводную в некоторой окрестности точки , Пусть  Пусть — произвольное положительное число, тогда: точкаприилипри:

Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

[править]Различные формы остаточного члена

В форме Лагранжа:

В форме Коши:

В интегральной форме:

Разложение основных элементарных функций

- Положив x₀=0 и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций:

• ; 

• ;

• ;

• ;

• ; 

• ;

• 

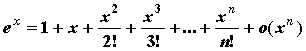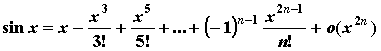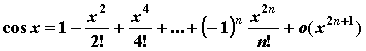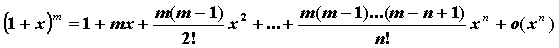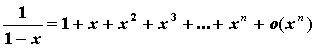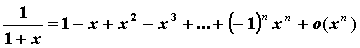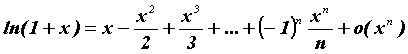
51 ВОПРОСЭкстремумы функции. Теорема Ферма. Необходимые и достаточные условия экстремума.

в точке x₀ функция достигает экстремума, если для любых x из некоторой окрестности точки x₀ выполняется неравенство f (x) ≤ f (x₀) (минимум) илиf (x) ≥ f (x₀) (максимум).

Теорема Ферма. Если функция f (x) дифференцируема в точке x0 и достигает в ней экстремума, то

Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю.

Обратное, вообще говоря, неверно. Так, точка x = 0 функции y = x³ не является ни максимумом, ни минимумом.

Точки, в которых производная функции равна нулю, называются стационарными точками функции. Точки, в которых производная функции равна нулю или не существует, называются критическими точками. Таким образом, все экстремумы являются критическими точками

Достаточные условия экстремума.

Пусть функция дифференцируема в некоторой окрестности точки x₀, кроме, быть может, самой этой точки, и непрерывна в точке x₀. Если производная функции меняет знак с минуса на плюс при переходе через эту точку слева направо, то x₀ – точка минимума. Если производная функции меняет знак с плюса на минус при переходе через эту точку слева направо, то x₀ – точка максимума.

52ВОПРОСВыпуклость и точки перегиба. Асимптоты графика функции.

Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x₁ и x₂ из этого отрезка 

Другими словами, если для любых точек x₁ и x₂ отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх.

Аналогично определяется функция, выпуклая вниз.

Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого

Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого 

Так, вторая производная функции равнаоткуда следует, что квадратичная функция выпукла вниз на всей области определения.

Пусть функция f (x) непрерывна в точке и имеет в этой точке конечную или бесконечную производную. Тогда точканазываетсяточкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.

Необходимое условие наличия точки перегиба. Если – точка перегиба функцииf (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то 

Достаточные условия наличия точки перегиба.

Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке Еслименяет знак при переходе через точкуто– точка перегиба функцииf (x).

Если то– точка перегиба функцииf (x).

Асимптоты графика функции

Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение 7.1   Вертикальной асимптотой графика функции называется вертикальная прямая, еслиилипри каком-либо из условий:,,. Заметим, что мы при этом не требуем, чтобы точкапринадлежала области определения функции, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:или, где.

Наклонной асимптотой графика функции приназывается прямая, если выполнены два условия: 1) некоторый луч целиком содержится в; 2) расстояние по вертикали между графиком и прямой стремится к 0 при :

(7.1)

Наклонной асимптотой графика функции приназывается прямая, если 1) некоторый луч целиком содержится в; 2) расстояние по вертикали между графиком и прямой стремится к 0 при 

В случае, если наклонная асимптота расположена горизонтально, то есть при , она называетсягоризонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая является горизонтальной асимптотой графикаприили, еслиилисоответственно.

53ВОПРОСОбщая схема исследования функции и построения её графика.

При построении графиков функций более сложного вида можно примерно придерживаться следующего плана.

1. Найти область определения и область значений функции.

2. Выяснить, является ли функция четной (нечетной).

3. Выяснить, является ли функция периодической.

4. Найти точку пересечения графика функции с осью ординат.

5. Найти нули функции и промежутки знакопостоянства.

6. Вычислить производную функции 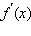и определить точки, в которых могут существовать экстремумы.

7. Найти промежутки монотонности функции.

8. Определить экстремумы функции.

9. Вычислить вторую производную 

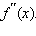
10. Определить точки перегиба.

11. Найти промежутки выпуклости функции.

12. Найти асимптоты графика.

13. Найти значения функции в нескольких контрольных точках.

14. Построить эскиз графика функции.

54ВОПРОСКривизна плоской кривой. Радиус кривизны. Понятие об эволюте и эвольвенте.

Плоскую кривую линию можно рассматривать как траекторию движения точки в плоскости; точка движется по касательной к кривой линии, обкатывая эту кривую без скольжения.

Движение точки вдоль кривой а связано с непрерывным изменением двух величин: расстояния S, на которое удалена точка от начального положения и угла a  поворота касательной  относительно начального положения.

Если с увеличением пути  S непрерывно увеличивается и a , кривая называется простой.

Угол a  (угол смежности) между касательными в двух бесконечно близких точках кривой, отнесенный к длине дуги между этими точками, определяет степень искривленности кривой линии, т.е. определяет кривизну кривой k.

,

предел отношения угла смежности касательных к соответствующей дуге.

Кривизна прямой в любой её точке равна нулю.

Кривизна произвольной кривой линии в различных точках различна, в отдельных точках она может быть равна нулю. Такие точки называются точками спрямления.

Кривизна в каждой из точек плоской кривой а определяется с помощью соприкасающейся в этой точке окружности

Соприкасающейся окружностью или кругом кривизны в данной точке называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки.

Центр соприкасающейся окружности называется центром кривизны кривой в данной точке, а радиус такой окружности – радиусом кривизны кривой линии в данной точке.

Множеством центров кривизны кривой является кривая линия - её называют эволютой данной кривой, а кривая по отношению к своей эволюте называется эвольвентой.

 

55ВОПРОСВекторная функция скалярного аргумента: определение, предел, непрерывность. Дифференцирование векторной функции. Геометрический и механический смысл производной.

Вектор-функция скалярных аргументов

     На множесве U задана вектор-функция, если с каждой его точкой M сопоставлен вектор . ЕслиU - множество точек на прямой и на ней введена декартова координата t, то вектор-функция на U является вектор-функцией одного скалярного аргумента ; еслиU - множество точек на плоскости и на ней введена декартова система координат Ouv, то имеем вектор-функцию двух скалярных аргументов.     Предел вектор-функции 

     - предел в точке, еслиЗапись:

     Если 

    Непрерывность вектор-функции 

     непрерывна в точке , еслиВектор-функция, непрерывная в каждой точке множестваU, называется непрерывной на множестве U.

     Дифференцирование вектор-функции       Производные вектор-функции 

     Если идифференцируемы, то:

     Дифференциал вектор-функции 

 Дифференцирование вектор-функции двух скалярных аргументов 

     Если инепрерывны, то=и