22. Правила Кирхгофа: физическое обоснование, формулировка, правила знаков; применение для расчета линейных электрических цепей, баланс мощностей.

Правила Кирхгофа— соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.^[1] Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U₁, I₁ есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает. i₂ + i₃ = i₁ + i₄Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

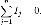
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений

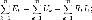
для переменных напряжений

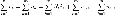
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Баланс мощности – система показателей, характеризующая соответствие суммы значений нагрузок потребителей энергосистемы (ОЭС) и необходимой резервной мощности величине располагаемой мощности энергосистемы.

23. Классическая теория проводимости: природа носителей тока в металлах; постулаты теории, дифференциальная форма законов Ома и Джоуля-Ленца.

Основные положения этой теории сводятся к следующим:

1). Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.

2). Поведение электронов подобно поведению молекул идеального газа (электронный газ).

3). При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.

4). При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.

При включении электрического поля на хаотическое движение электронов накладывается упорядоченное движение (называемое иногда «дрейфовым»), происходящее с некоторой средней скоростью ; возникает направленное движение электронов –электрический ток. Плотность тока определяется по формуле.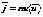

Оценки показывают, что при максимально допустимой плотности тока в металлах j = 10⁷ А/м² и концентрации носителей 10²⁸ – 10²⁹м^-3, . Таким образом, даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов.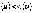

закона Ома в дифференциальной форме.

Здесь 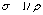–удельная электропроводность.

Размерность σ – [].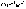

      Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость :

.

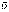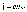      Обозначим 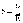, тогда;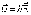

Теперь, если удельную электропроводность σ выразить через е, n и b: 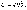то вновь получим выражениезакона Ома в дифференциальной форме:

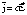
24. Собственная и примесная проводимость полупроводников: механизмы электронной и дырочной проводимости, донорные и акцепторные примеси, зависимость концентрации носителей тока от температуры. Терморезисторы.

Терморезистор — полупроводниковый резистор, в котором используется зависимость электрического сопротивления полупроводникового материала от температуры^[1]. Для терморезистора характерны большой температурный коэффициент сопротивления (ТКС) (в десятки раз превышающий этот коэффициент у металлов), простота устройства, способность работать в различных климатических условиях при значительных механических нагрузках, стабильность характеристик во времени. Терморезистор был изобретён Самюэлем Рубеном (SamuelRuben) в 1930 году. Различают терморезисторы с отрицательным (термисторы) и положительным (позисторы) ТКС. Их ещё называют NTC-термисторы и PTC-термисторы соответственно. У позисторов с ростом температуры растет и сопротивление, а у термисторов —- наоборот: при увеличении температуры сопротивление падает.

Режим работы терморезисторов зависит от того, на каком участке статической вольт-амперной характеристики (ВАХ) выбрана рабочая точка. В свою очередь ВАХ зависит как от конструкции, размеров и основных параметров терморезистора, так и от температуры, теплопроводности окружающей среды, тепловой связи между терморезистором и средой

Виды проводимости полупроводников

Полупроводниковые материалы имеют твердую кристаллическую структуру и по своему удельному сопротивлению, ) занимают промежуточную область между проводниками электрического тока, ) и диэлектриками.

Донорные примеси - атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию электронов. Донорными примесями являются химические элементы, внедренные в полупроводник с меньшей, чем у примеси, валентностью.

Акцепторные примеси - атомы химических элементов, внедренные в кристаллическую решетку полупроводника и создающие дополнительную концентрацию дырок. Акцепторными примесями являются химические элементы, внедренные в полупроводник с большей, чем у примеси, валентностью.