6. Поток и дивергенция векторного поля. Электростатическая теорема Гаусса для вакуума: интегральная и дифференциальная формы теоремы; ее физические содержание и смысл.

Электростатическая теорема Гаусса

Поток векторного поля

Гидростатическая аналогия:

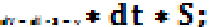
Для электростатического поля:

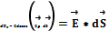
Поток вектора напряженности электростатического поля через поверхность пропорционален числу силовых линий, которые пересекают эту поверхность

Дивергенция векторного поля

Определение:

Единицы измерения:

Теорема Остроградского: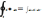

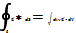
Физический смысл: расходимость вектора, указывает на наличие источников поля

Формулировка:

-Поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы пропорционален алгебраической сумме электрических зарядов тел или частиц, которые находятся внутри этой поверхности.

Физическое содержание теоремы:

*закон Кулона, поскольку является его прямым математическим следствием;

*полевая трактовка закона Кулона на основе концепции близкодействия электростатических взаимодействий;

*принцип суперпозиции электростатических полей

7.Применение электростатической теоремы Гаусса для расчета электростатических полей: общие принципы; расчет поля равномерно заряженной бесконечно длинной тонкой прямой нити и равномерно заряженной безграничной плоскости.

Применение электростатической теоремы Гаусса

Линейное распределение электрических зарядов

Расчет электростатического поля бесконечно длинной тонкой равномерно заряженной нити:

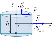
Алгоритм расчета электростатических полей:

• из соображений симметрии системы определяем форму силовых линий поля;

• выбираем удобную для нахождения потока форму замкнутой поверхности;

• находим поток вектора напряженности электростатического поля через эту поверхность;

• находим суммарный электрический заряд, который находится внутри этой поверхности;

• подставляем полученные значения в теорему Гаусса и находим напряженность поля

8. Циркуляция и ротор векторного поля. Работа сил электростатического поля: потенциальный характер электростатического поля; разность потенциалов между двумя точками поля, потенциал в заданной точке поля; эквипотенциальные поверхности; расчет потенциала поля, создаваемого неподвижным точечным зарядом; принцип суперпозиции для потенциала.

Потенциал электростатического поля в вакуме

Работа силы:

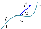
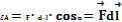
-криволинейный интеграл.

- циркуль вектора (интегральная хар.)

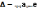
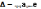; ; в-диф=бесконечно малому приращению.

Ротор векторного поля : (локальная характеристика). Разбираем поверхность, ограниченную , на элементарные площадки;

- циркуляция по контуру ;

- ротор вектора.

Rot векторной величины является вектор. Rot – вихрь.

Циркуляция приходящая на поверхность rot=0 когда проекция =0.

Если работа силы = 0, то и rot=0 и циркуляция.

Теорема Стокса:

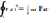
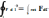циркуляция вектора по замкнутому контуру =потоку. Rot через поверхность ограниченную этим контуром.

циркул=0, то поле без вихревое.

Потенцианальный характер электрического поля.

Поскольку работа силы поля по перемещению в нем подобного электрический заряд не зависит от (перемещения) траектория движения, то электрического поля является потенциальной(безвихревым). Работа силы = 0.

только для поля неподвижного точечного заряда.

Разность потенциалов между 2-мя точками поля.

Разностью потенциалов или напряжением между 2-мя точками электростатического поля наз.отношение работы сил поля по перемещению пробного электрического заряда между данными точками к величине пробного заряда:

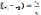
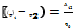
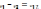
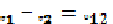
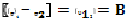
Потенциал в данной точке поля:

Если электростатическое поле создало точечным электрическим зарядом q тогда

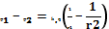
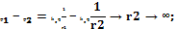
Потенциалом электростатического поля в точке называется отношение работы сил поля по перемещению пробного электрического заряда из данной точки в к величине этого пробного заряда:

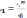– потенциал поля в точке определен только для поля тех зарядов, которые ограничены в пространстве; если не ограничены, то

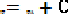
Эквипотенциальной поверхностью наз. совокупность точек поля с равным потенциалом.

Они применяют для графика изображения полей.

Вычисление потенциала:

Если электростатическое поле создано точечным электрическим зарядом q, тогда:

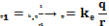
В соответствии с принципом суперпозиции электростатического поля потенциалы должны алгебраически суммированы:

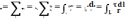
9. Градиент скалярной функции. Связь между напряженностью электростатического поля и его потенциалом: математическая запись и физический смысл для однородного и неоднородного полей; применение для расчета полей. Уравнение Пуассона.

ГРАДИЕНТ ФУНКЦИИ

и = f(x, у, z), заданной в некоторой обл. пространства (X Y Z), есть вектор с проекциями 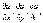обозначаемый символами: grad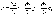гдеi, j, k — координатные орты. Г. ф. — есть функция точки (х, у, z), т. е. он образует векторное поле. Производная в направлении Г. ф. в данной точке достигает наибольшего значения и равна: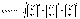 

Уравнение Пуассона— эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает

*электростатиче ское поле,

*стационарное поле температуры,

*поле давления,

*поле потенциала скорости в гидродинамике.

Это уравнение имеет вид: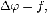 

В трёхмерной декартовой системе координат  уравнение принимает форму:

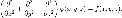
Нахождение φ для данного f — важная практическая задача, поскольку это обычный путь для нахождения электростатического потенциала для данного распределения заряда. В единицах системы СИ:

где — электростатический потенциал (ввольтах), — объёмнаяплотность заряда (в кулонах на кубический метр), а —диэлектрическая проницаемость вакуума (в фарадах на метр).