26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).

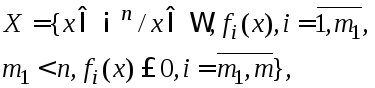Рассм.задачу(1), (2)

где - заданное мн-во и ф-ииопределены на.

Для задачи (1), (2) рассмю нормированную ф-цию Лагранжа: 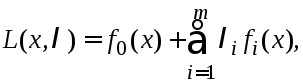(3)определенную на мн-ве (4)

Опр. Точканаз. седловой точкой функции Лагранжа (3), в области, если

Теорема1 (о седловой точке ф-ии Лагранжа) Пусть точка явлю седловой точкой ф-ции Лагранжа (3), тогда явлюрешение задачи (1)-(2).

Док-во: 1.Покажем сначала, что в условия теоремы точка уд. ограничениям (2) задачи (1)-(2). Т.к.-седловая точка ф-ции Лагранжа, то выполняется нер-ва:

(5)

Рассмю левое из (5):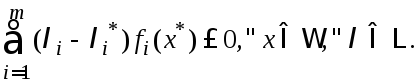(6)

В нер-во (6) подставляем

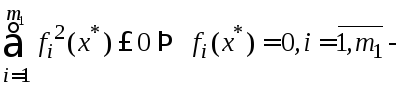вып-ся огранич. рав-ва.

Выберем некоторый индекс положимостальные. Подставим это в (6):выполняются ограничения неравенства.

Точка , т.к. она является седловой точкой функции Лагранжа. Т.е.удовл-ет огр-ям задачи (1)-(2).

2.Покажем, что для значения выполняется условие дополнительной нежесткости, а имеено, если

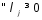Предположим противное: пусть для некоторого индексаВ нер-ве (6) положим, тогда получимпоследнее нер-во будет вып-ся дляа не длячто противоречит определению седловой точки.

3.Покажем, что точка - решение задачи (1)-(2). Рассмотрим правое из нер-в (5), из которого в силу условия дополнительной нежесткости

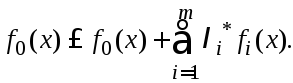
Рассмотрим последнее нер-во для:

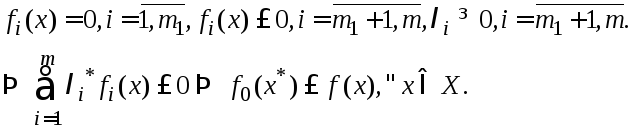Доказан

27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.

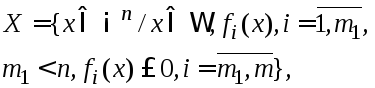Рассм.задачу (1), (2)

где -заданное мн-во и ф-ииопределены на.

Для задачи (1), (2) рассм. нормированную ф-ию Лагранжа: 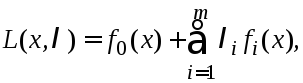(3) определенную на мн-ве

(4)

Теор2 (Критерий сущ.седловой точки ф-ии Лагранжа для задачи выпуклого прогр-ния) Пусть в задаче (1)-(2) функции являются выпуклыми, т.е задача (1)-(2)-задачи выпуклого программирования, (-выпуклое мн-во) и функцииявл. дифференцируемыми в точкеТогда точкаявл.седловой точкой ф-ции Лагранжа тогда и только тогда, когда

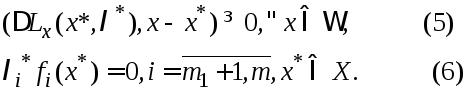
Док-во: (Необходимость). Пусть точка - седлова точка ф-ии Лагранжа, тогдаТ.к. ф-иидиф-мы, то ф-ия Лагранжа диф-ма:

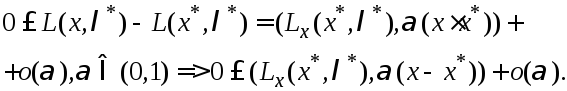
Последнее нер-во разделим на ,получим (5)

Покажем, что для значения вып-ся условие доп-ной нежесткости, а именно, если

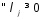Предположим противное: пусть для некоторого индексаВ нер-ве (6) положим, тогда получимпоследнее нер-во будет вып-ся дляа не длячто противоречит определению седловой точки.

Достаточность: Пусть вып-ся соотношения (5)-(6), покажем тогда, что точка явл-ся седловой точкой ф-ии Лагранжа. Т.к. ф-ии -выпуклые по условию теоремы, то ф-ия Лагранжа выпуклая по х.

По св-ву неотр-ти остатка для выпуклой ф-ии вып-ся:

т.е. правая точка из опр. седловой точки. Точка

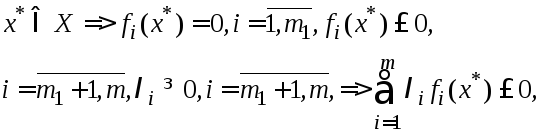
а из условия (6)

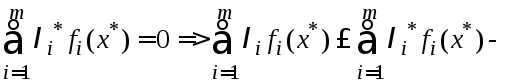отсюда следует правая часть нер-ва из определения седловой точки. Теорема доказана.

28.Определение двойственной задачи к задаче математического программирования.

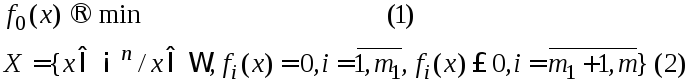
где заданное мн-во, ф-цииопределены на мн-веПереформулируем задачу (1) при помощи нормальной классической ф-ции Лагранжа: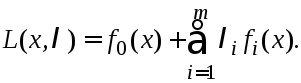Ф-ция Лагранжа определяется на мн-ве. Переформулируем задачу (1) при помощи нормальной классической ф-ции Лагранжа: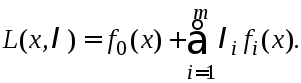

Ф-ция Лагранжа определена на мн-ве Рассм. Ф-цию

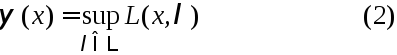
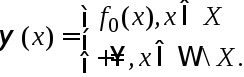
Рассм. задачу .

Точную нижнюю грань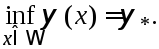В силу зависимости ф-иис задачей (1):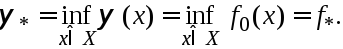В предположении, чтои мн-во решений задачи (1) не пусто, т.е.Задача (3) то же будет иметь мн-во решенийс тем жеmin значением.

Аналогично с функцией (2) рассмотрим ф-цию 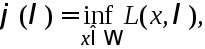которая будет определена наИ рассм. задачу

Задача (4) наз. двойственной к задаче (3) или к задаче (1). Переменные двойственные переменные,наз. основными.

При подстановке задачи (1) предполаг., что ф-ия приним. Конечные значения на мн-ве, поэтому ф-ия. Однако определение ф-иине исключает возможности принятия значений разных. Чтобы подчеркнуть конечность ф-ииговорят, что рассматривается задача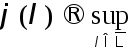(5)

гдеОбозначим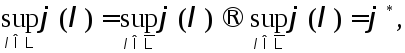и через

Теор Дляимеет место нер-во(6)

Док-во: По определению функции Если

то 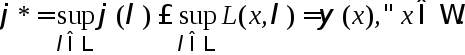Переходя в последнем нер-ве к точной нижней грани по мн-ву, получаем нер-воОстальные два нер-ва в (6) очевидны.

Теорема доказана.