
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
![]() (1)
(1)
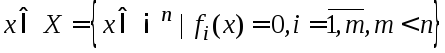 (1)
(1)
Т-ма1 Пусть
в задаче (1),(2) ф-ции
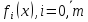 дважды
непр-но диф. Пусть точка
дважды
непр-но диф. Пусть точка![]() удовл. класс-му правилу множ-лей Л., т.е.
сущ.
удовл. класс-му правилу множ-лей Л., т.е.
сущ.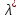 ,
что
,
что и пусть квадр-я форма вторых произв.
ф-ции Л. в т.
и пусть квадр-я форма вторых произв.
ф-ции Л. в т.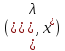 строго полож. опред. для всех ненулевых
векторов
строго полож. опред. для всех ненулевых
векторов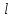 удовл. усл.
удовл. усл.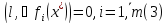 ,
т.е. для всех в-в
,
т.е. для всех в-в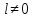 удовл.(3) выполн. нер-во
удовл.(3) выполн. нер-во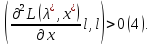 Тогда
Тогда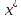 явл. т-кой строгого лок. минимума по
задаче (1)-(2).
явл. т-кой строгого лок. минимума по
задаче (1)-(2).


21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
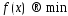 (1)
(1)
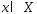 (2)
(2)
Если ф-ция
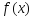 явл. выпуклой на выпуклом мн-веX,
то задача (1), (2) наз. задачей выпуклого
программирования.
явл. выпуклой на выпуклом мн-веX,
то задача (1), (2) наз. задачей выпуклого
программирования.
Опр:
Мн-во
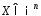 наз выпуклым, если для любых двух точек
наз выпуклым, если для любых двух точек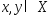 отрезок, соединяющий эти точки полностью
принадлежит этому мн-ву, т.е.
отрезок, соединяющий эти точки полностью
принадлежит этому мн-ву, т.е.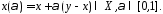 Примерами выпуклых мн-в могут служить
шар произвольного радиуса, гиперплоскоть,
все пр-ва.
Примерами выпуклых мн-в могут служить
шар произвольного радиуса, гиперплоскоть,
все пр-ва.
Опр:
Ф-ция
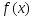 ,
определенная на выпуклом мн-ве Х, наз.
выпуклой, если для
,
определенная на выпуклом мн-ве Х, наз.
выпуклой, если для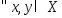 выполняется
выполняется
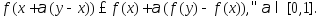 (1)
(1)
Замеч1: Если мн-во X явл. пустым или состоит из одной точки, то ф-цию, определенную на таком мн-ве, считают выпуклой.
Замеч2: Если знак нерав-ва в (1) заменить на противоположный, то ф-ции наз.вогнутой. При выполнении строгого неравенства ф-ция наз. строго выпуклой(Соответственно строго вогнутой ).
Примеры.
Ф-ция
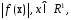 выпукла
выпуклаЛинейная ф-ция одновременно выпукла и вогнута.
Ф-ция
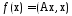 где А – симметричная неотрицательно
определенная матрица размерности
где А – симметричная неотрицательно
определенная матрица размерности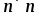 , и х – вектор размерности n, выпукла
, и х – вектор размерности n, выпукла
УТВ:сумма пересеч и умнож мн-ва на число явл. выпуклым мн-вами,если исходные мн-ва-выпуклые.
Пустое мн-во и мн-во состоящ из 1 точки удобно считать выпуклыми.
УТВ: сумма выпуклых ф-ций есть вып ф-ия.
Т1(сво-во
неотрицательности остатка)Пусть
ф-ция
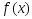 явл. выпуклой, дифференцируемой на
выпуклом мн-ве Х, тогда
явл. выпуклой, дифференцируемой на
выпуклом мн-ве Х, тогда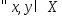 выполняется
выполняется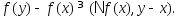
Док-во:
Т.к. ф-ция
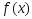 явл.выпуклой, то
явл.выпуклой, то
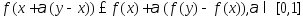 .
.
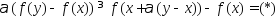
Т.к. ф-ция
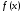 явл. дифференцируемой, то приращение
этой ф-ции можно разложить в ряд Тейлора:
явл. дифференцируемой, то приращение
этой ф-ции можно разложить в ряд Тейлора:
(*)=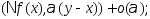
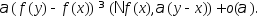
Последнее неравенство
делим на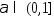 и устремим
и устремим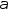 к 0. Теорема доказана.
к 0. Теорема доказана.
22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
Теор(о т. мин
в-ой ф-ии): Пусть
в задаче
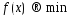 (1)
(1)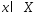 -(2)
ф-ия
-(2)
ф-ия
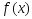 выпукла, определена на выпуклом мн-ве
Х, тогда:1)
каждая точка ее локального минимума
(если такая сущ-ет), явл-ся точкой
глобального минимума;
выпукла, определена на выпуклом мн-ве
Х, тогда:1)
каждая точка ее локального минимума
(если такая сущ-ет), явл-ся точкой
глобального минимума;
2)
Мн-во
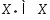 решений задачи (1), (2) явл-ся выпуклым;3)
если ф-ия
решений задачи (1), (2) явл-ся выпуклым;3)
если ф-ия
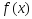 строго выпукла, то она может достичь
своегоmin
не более чем в одной точке.
строго выпукла, то она может достичь
своегоmin
не более чем в одной точке.
Док-во:
1)
Пусть
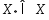 есть точка глобальнmin
ф-ии
есть точка глобальнmin
ф-ии
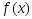 ,
т.е.
,
т.е. окрестность
этой точки
окрестность
этой точки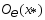 ,
так что
,
так что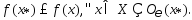 Пусть
Пусть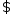 точка
точка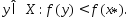 Соединим эти точки отрезком
Соединим эти точки отрезком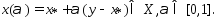 Т.к.
мн-во Х явл-ся выпуклым , то при всех
Т.к.
мн-во Х явл-ся выпуклым , то при всех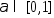 :
: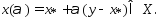
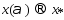 при
при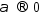 ,
след-но найдется такое значение
,
след-но найдется такое значение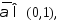 что
что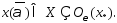 Поэтому
Поэтому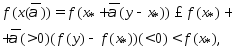
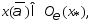 что противоречит
тому, что т.
что противоречит
тому, что т.
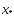 явл-ся точкой локальнmin.
явл-ся точкой локальнmin.
2)
Мн-во
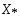 -
мн-во решений задачи
-
мн-во решений задачи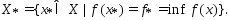 Пусть мн-во
Пусть мн-во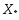 состоит более чем из одной точки. Возьмем
состоит более чем из одной точки. Возьмем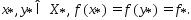
Рассм.
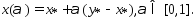 Т.к.ф-ия
Т.к.ф-ия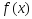 -выпукла,
то
-выпукла,
то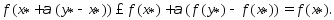
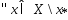 выполняется нер-во
выполняется нер-во
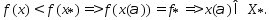
3)Предположим
сущ-ет точка
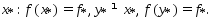 Соединим точки
Соединим точки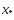 и
и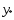 отрезком:
отрезком: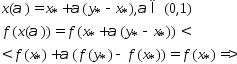
мы нашли точку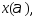 в которой
в которой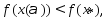 что противоречит тому, что
что противоречит тому, что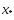 явл-ся точкой локальногоmin.
явл-ся точкой локальногоmin.
Т 2
(о ст-ной точке в-ой ф-ции):
Каждая стационарная точка выпуклой
ф-ции
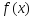 ,
определенная на выпуклом множестве Х,
явл. ее точкой минимума.
,
определенная на выпуклом множестве Х,
явл. ее точкой минимума.
Док-во:
Пусть
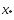 стационарная точка ф-ции
стационарная точка ф-ции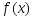 ,
т.е.
,
т.е.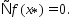 Рассмотрим произвольную точку
Рассмотрим произвольную точку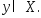 Для точек
Для точек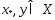 в силу выпуклости ф-ции
в силу выпуклости ф-ции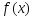 выполняется:
выполняется: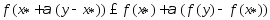 (3)Т.к.
ф-ция
(3)Т.к.
ф-ция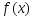 дифференцируема, то приращение (из
(3))=>
дифференцируема, то приращение (из
(3))=>
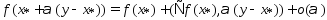 .
.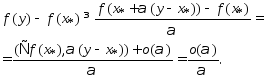 по
св-ву неотр
по
св-ву неотр
остатка
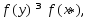
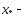 точка
минимума..
точка
минимума..
23. Необходимые усл. минимума дифференцируемой ф-ции на выпуклом мн-ве, выраженные через скалярное произведение. Критерий минимума выпуклой дифференцируемой функции на выпуклом множестве, сформулированный через скалярное произведение.
Замеч1.Если
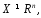 ф-ция
ф-ция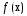 дифференцируема, но не обязательно
выпукла, то усл.
дифференцируема, но не обязательно
выпукла, то усл.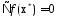 может не выполняться в точке минимума
ф-ции
может не выполняться в точке минимума
ф-ции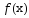 ,
т. к. возможна ситуация, когда точка
,
т. к. возможна ситуация, когда точка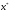 принадлежит границе мн-ваX.
принадлежит границе мн-ваX.
Теор1. Пусть
ф-ция
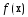 непрерывно дифференцируема на выпуклом
мн-веX.
Если точка
непрерывно дифференцируема на выпуклом
мн-веX.
Если точка
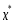 явл. ее точкой минимума, то для всех
явл. ее точкой минимума, то для всех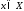 выполняется нерав-во
выполняется нерав-во
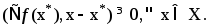 (1)
(1)
Док – во. Пусть
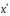 - точка минимума ф-ции
- точка минимума ф-ции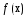 .
Тогда сущ.
.
Тогда сущ.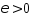 ,
такое что
,
такое что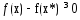 для всех
для всех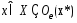 .
Выберем произвольную точку
.
Выберем произвольную точку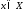 и рассмотрим отрезок
и рассмотрим отрезок
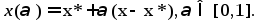
Т. к. мн-во X
выпукло, то этот отрезок принадлежит
мн-ву X
и при малых
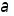
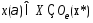 .
Для таких
.
Для таких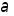 рассм.
рассм.
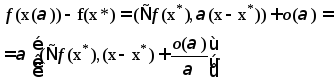 (2)
(2)
Последнее выражение
является неотрицательным, так как x*
есть тока минимума. Но тогда
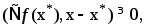 как
и в противном случае при достаточно
малых
как
и в противном случае при достаточно
малых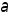 приращение (3) изменит свой знак на
противоположный. Теор. доказана.
приращение (3) изменит свой знак на
противоположный. Теор. доказана.
Следстивие 1.Если
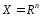 или
или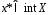 ,то
нер-во (1) превращается в равенство
,то
нер-во (1) превращается в равенство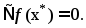
Следствие 2.Усл(2) можно записать в виде
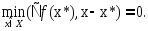 (3)
(3)
Теор2.
Для того, чтобы выпуклая, непрерывно
дифференцируемая ф-ция
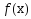 , определенна на выпуклом, замкнутом
мн-ве Х, достигала своего минимума в
точке
, определенна на выпуклом, замкнутом
мн-ве Х, достигала своего минимума в
точке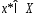 ,
необходимо и достаточно, чтобы выполнялось
нерав-во
,
необходимо и достаточно, чтобы выполнялось
нерав-во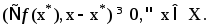
Док-во: Необходимость
следует из теор1. Докажем достаточность.
Пусть точка x*
такова, что выполнена усл.
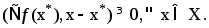 Возьмем
произвольную точку
Возьмем
произвольную точку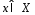 и рассмотрим
и рассмотрим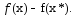 По св-ву неотрицательного остатка имеем
По св-ву неотрицательного остатка имеем
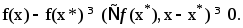
Замечание 4.Форма (3) необходимого усл. минимума непрерывно дифференцируемой ф-ции на выпуклом замкнутом мн-ве используется для построения метода усл. градиента.
24.Задача проектирования на выпуклое и замкнутое множество. Свойства проекции. Примеры.
Опр.
Расстояние от точки
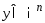 до
мн-ва
до
мн-ва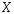 определ.
формулой
определ.
формулой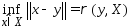 .Ф-ция
.Ф-ция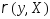 непр.
поy.
непр.
поy.
Опр.
Проекцией точки y
на мн-во X
наз. такая точка
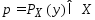 ,
для кот.
,
для кот.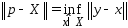
Задача нахождения
точки p
наз задачей
проектирования точки y
на мн-во X.
Если решение задачи проектирования
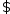 ,
то норма
,
то норма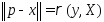
 Задачу
проектир. обычно заменяют равносильной
задачей
Задачу
проектир. обычно заменяют равносильной
задачей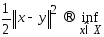 (1)
(1)
Задача (1) предст. собой задачу min-ции квадратичной ф-ции
Утв1.
Если мн-во
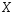 явл.
Замкнутым и не пустым, то
явл.
Замкнутым и не пустым, то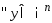
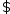
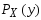 и
если
и
если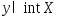 ,
то
,
то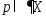
Док-во.
Пусть
 .
В противном сл.
.
В противном сл.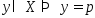 .
Рассм. произв. точку
.
Рассм. произв. точку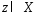 и
построим мн-во
и
построим мн-во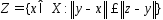 .
Мн-во
.
Мн-во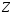 не
явл. пустым, явл. замкнутым и огранич.
Поэтому по теор. Вейерштрасса
не
явл. пустым, явл. замкнутым и огранич.
Поэтому по теор. Вейерштрасса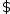 проекция точкиy
на Z.
В силу постр. мн-ва Z:
проекция точкиy
на Z.
В силу постр. мн-ва Z: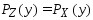 .
Пусть
.
Пусть
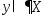
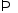
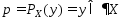 ,
,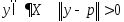 .
.
Предп. противное.
 .
Тогда
.
Тогда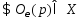 .
Рассм. отрезок, соед. точкиy
и p:
.
Рассм. отрезок, соед. точкиy
и p:
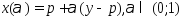 .
Найдется такое
.
Найдется такое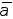 ,
что при
,
что при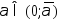
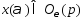 .
Рассм. расстояние
.
Рассм. расстояние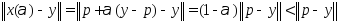
След-но, p не явл. проекцией.
Утв2.
Если
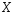 непустое,
выпуклое и замкнутое, то
непустое,
выпуклое и замкнутое, то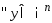
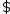 ед. проекция
ед. проекция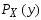
Док-во.
Пусть
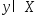 .
Тогда очевидно, что
.
Тогда очевидно, что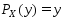 ,
поэтому явл. ед. Рассм., когда
,
поэтому явл. ед. Рассм., когда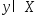 .
Предп., что
.
Предп., что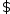 более одной проекции
более одной проекции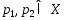 ,
,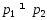 ,
,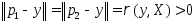
Вектора
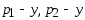 не
явл. коллинеарными. Действ-но, если
не
явл. коллинеарными. Действ-но, если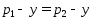 ,
то
,
то .
Если
.
Если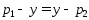 ,
то
,
то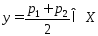 .
Это противоречит тому, что
.
Это противоречит тому, что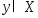 .Рассм.
.Рассм.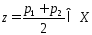 .
.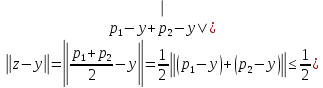
Нашли точку
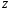 ,
такую
,
такую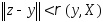 ,
что противор., что
,
что противор., что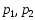 -проекции.Замеч.
Если мн-во не явл. выпуклым, то может
сущ. две проекции. Рассм. примеры
нахождения проекций точек на мн-ва для
некот. конкр. мн-в
-проекции.Замеч.
Если мн-во не явл. выпуклым, то может
сущ. две проекции. Рассм. примеры
нахождения проекций точек на мн-ва для
некот. конкр. мн-в
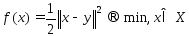
1)
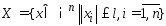 ;
2)
;
2)
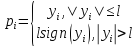 ;
;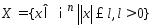
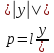 ;3)
;3)
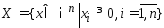
 ;
4)
;
4)
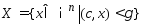
Т.к. проекция в
любой точке, не принадл. X,
будет принадл. границе мн-ва X,
то от данной задачи можно перейти к
задаче min-ции
ф-ции f(x)
при ограничении
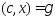 .
Т.к.c-ненулевой
вектор, сост. классич. ф-цию Лагранжа
.
Т.к.c-ненулевой
вектор, сост. классич. ф-цию Лагранжа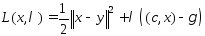 .Система
необх. усл:
.Система
необх. усл: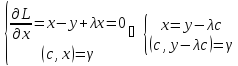 ;
;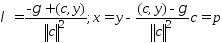
25. Критерий построения проекции на выпуклое замкнутое множество. Необходимые усл. минимума диф. ф-ции на выпуклом мн-ве, выраженные в терминах проекции точки на мн-во. Критерий минимума выпуклой диф. ф-ции на выпуклом мн-ве, сформулированный с помощью оператора проектирования.
Теор1.Пусть
непустое мн-во X
явл. выпуклым и замкнутым. Тогда точка
р
явл. проекцией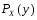 точки у на мн-воX
только тогда, когда выполняется усл.
точки у на мн-воX
только тогда, когда выполняется усл.
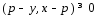 для всех
для всех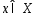 .
.
Док-во.
Рассм.
ф-цию
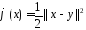 .
Эта ф-ция явл. квадратичной, выпуклой.
Мн-воX
по усл. Тео. замкнуто и выпукло. Поэтому
.
Эта ф-ция явл. квадратичной, выпуклой.
Мн-воX
по усл. Тео. замкнуто и выпукло. Поэтому
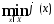 достигается в точке
достигается в точке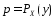 эта точка явл.единственной. Тогда по
теореме о необходимых и достаточных
условиях минимума выпуклой ф-ции на
замкнутом, выпуклом мн-ве выполняется
усл.
эта точка явл.единственной. Тогда по
теореме о необходимых и достаточных
условиях минимума выпуклой ф-ции на
замкнутом, выпуклом мн-ве выполняется
усл. для всех
для всех .
.
Но
в данном случае
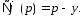 Тем самым теор. доказана.
Тем самым теор. доказана.
В следующих теоремах выясняется зависимость решения задачи математического программирования и решения задачи проектирования.
Теор2.
Пусть точка
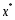 есть точка локального минимума ф-ции
есть точка локального минимума ф-ции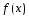 на
множестве X.
Функция
на
множестве X.
Функция
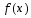 предполагается
непрерывно дифференцируемой, а мн-во X
выпуклым и замкнутым. Тогда для
произвольного
предполагается
непрерывно дифференцируемой, а мн-во X
выпуклым и замкнутым. Тогда для
произвольного
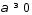 справедливо равенство
справедливо равенство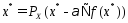 .Док-во.
Пусть
.Док-во.
Пусть
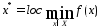 .
Тогда
выполняется усл.
.
Тогда
выполняется усл.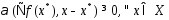 (1)Пусть
(1)Пусть
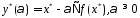 .
Преобразуем последнее равенство к виду
.
Преобразуем последнее равенство к виду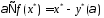 и подставим в формулу (1). Получим
и подставим в формулу (1). Получим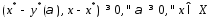 .
Тогда по теор1 заключаем, что
.
Тогда по теор1 заключаем, что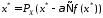 .
Теорема доказана.
.
Теорема доказана.
Теор3.
Пусть ф-ция
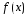 явл. выпуклой, непрерывно дифференцируемой,
мн-воX
выпуклым и замкнутым. Точка
явл. выпуклой, непрерывно дифференцируемой,
мн-воX
выпуклым и замкнутым. Точка
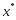 есть точка локального минимума
есть точка локального минимума для
произвольного
для
произвольного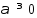 справедливо рав-во
справедливо рав-во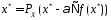 .
.
Док-во. Необходимость следует из теоремы 2.
Докажем
достаточность. Пусть выполняется усл.
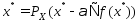 .
Тогда по теореме 1 имеем
.
Тогда по теореме 1 имеем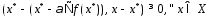 из чего следует
из чего следует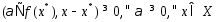 и
и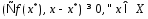 .
.
Тогда
по критерию локального минимума выпуклой
ф-ции на замкнутом выпуклом мн-ве
заключаем, что
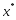 есть
точка локального минимума ф-ции
есть
точка локального минимума ф-ции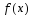 на мн-веХ.
Теорема доказана.
на мн-веХ.
Теорема доказана.
