
- •1.Понятие решения задачи мат. Программиров.
- •2. Основн. Формы злп. Правила сведения злп к канон.Форме. Геометр.Интерпретация злп. Понятие угловой точки мн-ва.
- •4. Определение базиса угловой точки. Невырожденные угловые точки. Примеры.
- •5. Связь между переменными задачи лп
- •6. Формула приращения целевой функции злп.
- •7. Достаточное условие оптимальности в злп. Достаточное условие неразрешимости злп
- •8. Итерация симплекс–метода
- •11. Нахождение базиса угловой точки. Пример
- •12. Постановка тз. Построение нач. Плана перевозок методом северо-западного угла, методом мин. Элемента.
- •13. Определение закрытой модели тз. Критерий существования решения тз.
- •14. Исследование мн-ва клеток транспортной таблицы
- •15. Достаточное условие минимальности стоимости перевозок
- •16. Классический метод решения задачи безусловной минимизации функции многих переменных. Пример.
- •17. Метод исключения решения задачи на условный минимум. Пример.
- •18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
- •19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
- •20. Достаточные условия экстремума в задаче оптимизации с ограничениями типа равенств
- •21.Опр-ия выпуклого мн-ва, выпуклой функции. Св-ва выпуклых множеств. Сумма выпуклых функций. Св-во неотрицательности остатка выпуклой функции
- •22.Теорема о точках минимума выпуклой функции. Теорема о стационарной точке выпуклой функции
- •26.Теорема о седловой точке функции Лагранжа (достаточные условия оптимальности).
- •27. Критерий существования седловой точки функции Лагранжа для задачи выпуклого программирования.
- •28.Определение двойственной задачи к задаче математического программирования.
- •29. Связь между двойственной и прямой задачами математического программирования.
- •30.Пример решения задачи оптимизации с помощью теории двойственности
- •31.Основные определения в задаче одномерной минимизации. Примеры.
- •33. Метод золотого сечения решения задачи одномерной минимизации.
- •34. Обоснование метода ломаных решения задачи одномерной минимизации.
- •35. Алгоритм и условия сходимости метода ломаных решения задачи одномерной минимизации. Пример. Описание метода ломаных
- •36.Алгоритм метода скорейшего спуска решения змм.
- •37.Алгоритмы метода условного градиента и метода проекции градиента решения задачи многомерной условной минимизации.
- •38.Алгоритм метода покоординатного спуска решения задачи многомерной минимизации. Геометрическая иллюстрация.
- •39.Сходимость метода скорейшего спуска.
- •41. Метод вариаций Лагранжа
- •42. Уравнение Эйлера
- •43. Случаи интегрируемости ур-ния Эйлера. Примеры.
- •44.Задача вариационного исчисления с незакрепленными концами и фиксированным отрезком интегрирования.
- •45.Задача вариационного исчисления с незакрепленными концами и нефиксированным отрезком интегрирования
- •46. Задача вариационного исчисления с движущимся по кривой концом.
- •47. Примеры задач динамического программирования, их особенности
- •48.Принципы динамического программирования и функциональные уравнения Беллмана.
18. Обобщенное правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств.
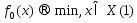
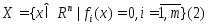
Ф-ей Лагранжа в з.(1), (2) наз. ф-ия
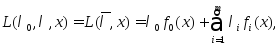
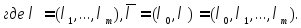
Вектор
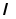 наз.
в-ом множ-лей Лагранжа,
наз.
в-ом множ-лей Лагранжа,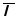 -обобщенным
в-ом мн-лей Лагранжа.
-обобщенным
в-ом мн-лей Лагранжа.
Т-ма1(обобщ.правило
мн.Л.) Пусть
точка
![]() явл
реш-м з.(1),(2), и пусть ф-ции
явл
реш-м з.(1),(2), и пусть ф-ции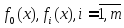 непр-но диф. В окрестности т.
непр-но диф. В окрестности т.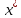 ,тогда
сущ. Такие числа
,тогда
сущ. Такие числа
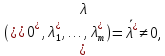 что
что
Д-во.
Т.к. в рав-ах (3)
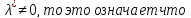
![]()
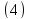 - ЛЗ.Предпол-м прот-ое. Пусть система
векторов (4) ЛНЗ.Тогда их кол-во не
превосходит размерности пространства,
т.е.
- ЛЗ.Предпол-м прот-ое. Пусть система
векторов (4) ЛНЗ.Тогда их кол-во не
превосходит размерности пространства,
т.е.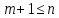 .
Если
.
Если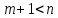 ,
то систему в-ов(4) дополним нек-ми векторами
так обр., чтобы получ.с-ма в-ов
,
то систему в-ов(4) дополним нек-ми векторами
так обр., чтобы получ.с-ма в-ов
![]() (5)оставалась ЛНЗ. Построим ф-ии, зав-щие
от переменныхx
и t:
(5)оставалась ЛНЗ. Построим ф-ии, зав-щие
от переменныхx
и t:
![]() ,
,![]() ;
;![]() .Рассм.
.Рассм.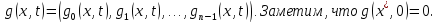
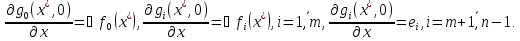 Тогда по т-ме о
неявныхдля ф-циях найд.
Тогда по т-ме о
неявныхдля ф-циях найд.
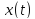 ,для
которой вып.усл.1)
,для
которой вып.усл.1)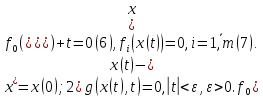 Т.е.
ф-ия
Т.е.
ф-ия
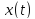 удовлетворяет ограничениям з-чи и при
удовлетворяет ограничениям з-чи и при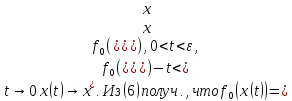 т.е.
нашли такую ф-ю
т.е.
нашли такую ф-ю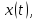 удовл-щую
огран-ям з-чи в кот., знач. цел.ф-ии
строго<чем
удовл-щую
огран-ям з-чи в кот., знач. цел.ф-ии
строго<чем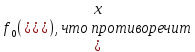 тому ,что
тому ,что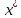 -явл.
реш-м з.(1),(2).
Зам1.
Поиск точек мин-ма начинается с реш-я
с-мы уравн-й относительно
-явл.
реш-м з.(1),(2).
Зам1.
Поиск точек мин-ма начинается с реш-я
с-мы уравн-й относительно
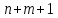 -переменной
величины, состоящей из урав-й(3) и урав-й
из (2).
-переменной
величины, состоящей из урав-й(3) и урав-й
из (2).
Если
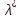 есть решение с-мы(3), то
есть решение с-мы(3), то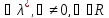 явл. реш-м ур.(3). Т.е.множ-ли Лагранжа
удовл-щие соотнош.(3) опред-ся с точностью
до постоянного множителя, поэтому при
реш-ии с-мы необ-х условий согласно
обобщ-му правилу множ-лей Лагранжа
дост-но рассм-ть случаи
явл. реш-м ур.(3). Т.е.множ-ли Лагранжа
удовл-щие соотнош.(3) опред-ся с точностью
до постоянного множителя, поэтому при
реш-ии с-мы необ-х условий согласно
обобщ-му правилу множ-лей Лагранжа
дост-но рассм-ть случаи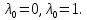
19. Классическое правило множителей Лагранжа в задаче оптимизации с ограничениями типа равенств. Необходимые условия второго порядка в задаче оптимизации типа равенств.
![]() (1)
(1)
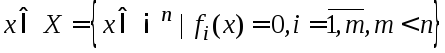 (2)
(2)
Опр.
Задача (1),(2) наз нормальной в точке
![]() ,
если среди обобщенных векторов множ-лей
Л., соотв. в точке
,
если среди обобщенных векторов множ-лей
Л., соотв. в точке![]() нет таких для кот.
нет таких для кот.![]() ,
то вектор
,
то вектор![]() в таком случае наз. норм-ным.
в таком случае наз. норм-ным.
Опр. Точка
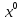 наз. обыкновенным планом для задачи
(1)-(2), если
наз. обыкновенным планом для задачи
(1)-(2), если
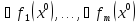 -ЛНЗ(3).
Усл. (3) наз. условием Люстерика.
-ЛНЗ(3).
Усл. (3) наз. условием Люстерика.
Т-ма1Оптим.
план
![]() для з.(1),(2) явл нормальнам тогда и только
тогда, когда он обыкновенный.
для з.(1),(2) явл нормальнам тогда и только
тогда, когда он обыкновенный.
Д-во:Пусть
![]() -оптим.
норм. план. Это значит, что сущ. вектора
-оптим.
норм. план. Это значит, что сущ. вектора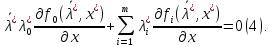 Среди которых
Среди которых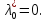 Предположим, что при этом
Предположим, что при этом
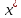 не явл. обыкновенным, это означает
не явл. обыкновенным, это означает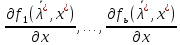 – ЛЗ.
– ЛЗ.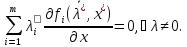 Тогда
соотнош.(4) возможно при усл.
Тогда
соотнош.(4) возможно при усл.
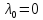 ,
что
,
что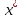 -нормальный
план.
-нормальный
план.
Пусть план
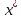 явл. обыкнов., тогда вектора
явл. обыкнов., тогда вектора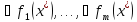 -ЛНЗ.
План
-ЛНЗ.
План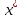 явл. оптимальным, то согласно обобщ-му
правилу множ-лей Лагранжа сущ. множитель
(
явл. оптимальным, то согласно обобщ-му
правилу множ-лей Лагранжа сущ. множитель
(![]() ,)
,)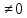 ,что
вып. рав-во
,что
вып. рав-во
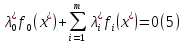 .
.
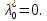 Предпол.,
что план
Предпол.,
что план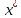 не явл. не явл. нормальным. Но в силу
того, что среди множ-лей Л. есть не нулевые
из (5) следует что градиенты огран-ий ЛЗ,
что противоречит обыкновенности плана
не явл. не явл. нормальным. Но в силу
того, что среди множ-лей Л. есть не нулевые
из (5) следует что градиенты огран-ий ЛЗ,
что противоречит обыкновенности плана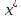 .
.
Т-ма2(классич.
правило мн. Л.)
Пусть
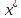 оптим. План з-чи (1),(2) и пусть при
оптим. План з-чи (1),(2) и пусть при
 ,
,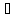 ограничений
ограничений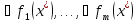 -ЛНЗ. Тогда сущ. ед-ный в-р множ-лей Л.
(
-ЛНЗ. Тогда сущ. ед-ный в-р множ-лей Л.
(![]() ),
такой, что справедливы рав-ва
),
такой, что справедливы рав-ва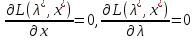 (6).
(6).
Док-во.
В усл. т-мы 2 план
![]() явл обыкн., след-но по т-ме 1 норм., тогда
1 из усл.(6) есть усл. из обобщ-го правила
множлей Л. при условии,
явл обыкн., след-но по т-ме 1 норм., тогда
1 из усл.(6) есть усл. из обобщ-го правила
множлей Л. при условии,![]() .
, 2 из (6) совпадает с системой ограничений.
.
, 2 из (6) совпадает с системой ограничений.
Т-ма3.(необх. Усл.
2-го порядка) Пусть
ф-я
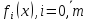 зад. (1)-(2) дважды непрерывно диф., если
т.
зад. (1)-(2) дважды непрерывно диф., если
т.
![]() явл. т. лок. мин-ма этой з-чи и явл. обыкн-й
т. с-мы огран-й и
явл. т. лок. мин-ма этой з-чи и явл. обыкн-й
т. с-мы огран-й и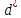 есть соотв. В-р множ-лей Л., тогда квадр-я
форма, составленная по вторым произ.
ф-ции Л. по переменным задачи выполненным
в т.
есть соотв. В-р множ-лей Л., тогда квадр-я
форма, составленная по вторым произ.
ф-ции Л. по переменным задачи выполненным
в т.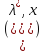 не отриц. опред. Для всех в-ров
не отриц. опред. Для всех в-ров
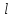 удовл. условиям
удовл. условиям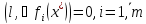 (7),
т.е. для всех в-ров
(7),
т.е. для всех в-ров
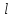 удовл.(7) выполн.(8)
удовл.(7) выполн.(8)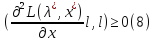 .
.
