Перевод чисел из любой системы счисления в 10 чную систему счисления

При переводе числа из любой системы счисления в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Пример

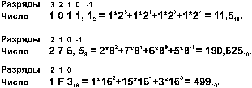
Перевод чисел из 8, 16-чной системы счисления в 2-чную систему счисления

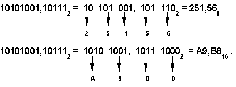
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Пример

Перевод чисел из 2-чной системы счисления в 8,16-чную систему счисления

Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

Пример

Арифметические действия над числами в любой позиционной системе счисления

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе счисления, т.к.все они основываются на правилах выполнения действий над соответствующими полиномами.

Пример 1 Сложим числа 15 и 6 в 10-чной, 2-чной, 8-чной, 16-чной системах счисления.

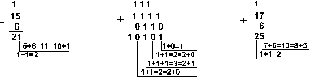
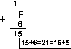
Пример 2 Вычтем число 59,75 из числа 201,25 в 10-чной, 2-чной, 8-чной, 16-чной системах счисления.

Пример 3 Перемножим числа 115 и 51 в 10-чной, 2-чной, 8-чной системах счисления.

Пример 4 Разделим число 30 на число 6 в 10-чной, 2-чной, 8-чной системах счисления.

Перевод чисел из десятичной системы в восьмеричную

Для перевода чисел из десятичной системы счисления в восьмеричную используют тот же "алгоритм замещения", что и при переводе из десятичной системы счисления в двоичную, только в качестве делителя используют 8, основание восьмеричной системы счисления:

1. Делим десятичное число А на 8. Частное Q запоминаем для следующего шага, а остаток a записываем как младший бит восьмеричного числа.

2. Если частное q не равно 0, принимаем его за новое делимое и повторяем процедуру, описанную в шаге 1. Каждый новый остаток записывается в разряды восьмеричного числа в направлении от младшего бита к старшему.

3. Алгоритм продолжается до тех пор, пока в результате выполнения шагов 1 и 2 не получится частное Q = 0 и остаток a меньше 8.

Например, требуется перевести десятичное число 3336 в восьмеричное. В соответствии с приведенным алгоритмом получим:

333610 : 8 = 41710

333610 - 333610 = 0, остаток 0 записываем в МБ восьмеричного числа.

41710 : 8 = 5210

41710 - 41610 = 1, остаток 1 записываем в следующий после МБ разряд восьмеричного числа.

5210 : 8 = 610

5210 - 4810 = 4, остаток 4 записываем в старший разряд восьмеричного числа.

610 : 8 = 010, остаток 0, записываем 6 в самый старший разряд восьмеричного числа.

Таким образом, искомое восьмеричное число равно 6410₈.