
- •Пособие по математике
- •Глава 1. Производная
- •§1. Определение производной.
- •§2. Правила дифференцирования
- •1. Дифференцирование явных функций.
- •2. Дифференцирование неявной функции.
- •3. Дифференцирование функций, заданных параметрически.
- •4. Производные высших порядков.
- •Глава 2. Приложение производной
- •§1. Дифференциал функции
- •§2. Правило лопиталя
- •§3. Возрастание и убывание функции. Экстремум функции
- •5. Второе достаточное условие экстремума.
- •3.5. 3.6.
- •3.7. 3.8.
- •§4. Наибольшее и наименьшее значения функции на отрезке
- •§5. Выпуклость графика функции. Точки перегиба
- •2. Достаточное условие выпуклости вверх (вниз).
- •4. Необходимое условие точки перегиба.
- •5. Достаточное условие точки перегиба.
- •§6. Исследование функций и построение их графиков
- •6.4. 6.5.
- •6.6. 6.7.
- •6.8. 6.9.
- •§7. Задачи для самостоятельной работы
§5. Выпуклость графика функции. Точки перегиба
1.
График функции
![]() имеет на интервале
имеет на интервале![]() выпуклость
вверх (вниз),
если на этом интервале график расположен
не выше (не ниже) касательной к графику
функции, проведенной к любой точке этого
интервала.
выпуклость
вверх (вниз),
если на этом интервале график расположен
не выше (не ниже) касательной к графику
функции, проведенной к любой точке этого
интервала.
Изобразим графики выпуклых вверх и вниз функций:
Выпуклость вверх Выпуклость вниз


Допустимо называть выпуклую вверх функцию просто выпуклой, а выпуклую вниз функцию вогнутой.
При краткой записи используются обозначения
-

Выпуклая вверх функция

Выпуклая вверх функция
2. Достаточное условие выпуклости вверх (вниз).
Если функция
![]() в каждой точке интервала
в каждой точке интервала![]() имеет
имеет![]()
![]() то график функции имеет на интервале
то график функции имеет на интервале![]() выпуклость вверх (вниз).
выпуклость вверх (вниз).
3.
Если в точке
![]() график функции
график функции![]() выпуклость вверх меняет на выпуклость
вниз или наоборот, то точка
выпуклость вверх меняет на выпуклость
вниз или наоборот, то точка![]() называетсяточкой
перегиба.
называетсяточкой
перегиба.
На графиках укажем точки перегиба:


![]() - точка перегиба.
- точка перегиба.
4. Необходимое условие точки перегиба.
Если в точке
![]() график функции
график функции![]() имеет точку перегиба, а сама функция
имеет непрерывную вторую производную,
тогда
имеет точку перегиба, а сама функция
имеет непрерывную вторую производную,
тогда![]() в точке
в точке![]() обращается в ноль:
обращается в ноль:
![]()
Точки графика, в которых вторая производная равна нулю, или не существует, называются критическими точками II рода.
5. Достаточное условие точки перегиба.
Пусть функция
![]() дважды дифференцируема в некоторой
окрестности точки
дважды дифференцируема в некоторой
окрестности точки![]()
![]() и при переходе через эту точку вторая
производная меняет знак. Тогда точка
и при переходе через эту точку вторая
производная меняет знак. Тогда точка![]() является точкой перегиба графика функции
является точкой перегиба графика функции![]()
Запишем схематически достаточное условие точки перегиба:


знак
![]() знак
знак![]()
поведение поведение
графика y графика y
![]()
![]() - точка перегиба.
- точка перегиба.
5.1.
Найти точки перегиба, интервалы выпуклости
вверх и выпуклости вниз графика функции
![]()
Решение. Имеем
![]() функция дважды дифференцируема на всей
числовой оси. Определим критические
точки второго рода:
функция дважды дифференцируема на всей
числовой оси. Определим критические
точки второго рода:![]()
![]() т.е.
т.е.![]()
![]()
Для определения
знака второй производной проведем
разложения
![]()
Определим знак второй производной:
з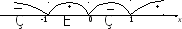 нак
нак![]()
поведение графика
На множестве
![]() график функции выпуклый вверх. На
множестве
график функции выпуклый вверх. На
множестве![]() график функции выпуклый вниз. Точки
график функции выпуклый вниз. Точки![]()
![]()
![]() являются точками перегиба. ►
являются точками перегиба. ►
Найти интервалы выпуклости и точки перегиба графиков функций:
5.2.
![]()
5.3.
![]()
5.4.
![]()
§6. Исследование функций и построение их графиков
При построении графиков функций рекомендуется последовательно рассматривать следующие вопросы:
Найти область определения функции.
Исследовать функцию на четность.
Исследовать функцию на периодичность.
Исследовать функцию на непрерывность.
Исследовать функцию на наличие асимптот.
Исследовать функцию на монотонность и экстремум.
Исследовать функцию на выпуклость и точки перегиба.
Найти точки пересечения графика функции с осями координат.
Для уточнения графика вычислить координаты дополнительных точек.
Пункты 2, 3 и 5 для некоторых видов функций опускаются.
6.1.
Исследовать функцию
![]() и построить ее график.
и построить ее график.
Решение.
Функция определена на всей числовой оси.
 т.е. функция четная,
ее график симметричен относительно
оси
т.е. функция четная,
ее график симметричен относительно
оси
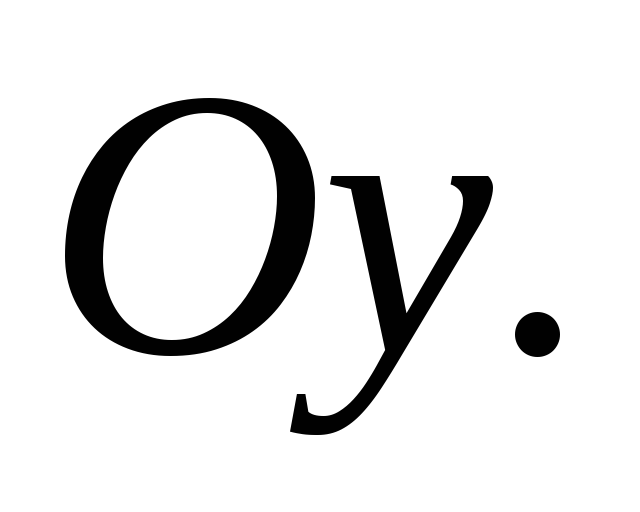
Исследование на периодичность не проводится.
Функция непрерывна во всех точках. Вертикальных асимптот нет.
 Горизонтальных
асимптот нет.
Горизонтальных
асимптот нет.
Так как
![]() то наклонных асимптот нет.
то наклонных асимптот нет.
Точки
![]()
![]() являются критическими. Покажем знак
первой производной:
являются критическими. Покажем знак
первой производной:

знак
![]()
поведение y
Функция y
возрастает
на множестве
![]()
Функция y
убывает на множестве
![]()
Точки
![]() и
и![]() являются точками максимума функций.
Точка
являются точками максимума функций.
Точка![]() является точкой минимума функции.
Находим значения функции в точках
локального экстремума:
является точкой минимума функции.
Находим значения функции в точках
локального экстремума:![]()
![]()
![]()
7 .
.![]()
![]() при
при![]() Определяется знак второй производной:
Определяется знак второй производной:
знак
![]()
поведение y
Функция выпукла
вверх на множестве
![]() Функция выпукла вниз на множестве
Функция выпукла вниз на множестве![]() Точки
Точки![]()
![]() являются точками перегиба. Находим
значения функции в точках перегиба
являются точками перегиба. Находим
значения функции в точках перегиба![]()
8. Определим точки пересечения с осями координат:
1)
![]() График функции проходит через начало
координат.
График функции проходит через начало
координат.
2)
![]()
![]() т.е.
т.е.![]()
![]() Точками пересечения с осью абсцисс
являются точки
Точками пересечения с осью абсцисс
являются точки![]()
![]()
![]()
Строим график функции

►
6.2.
Исследовать функцию
![]() и построить ее график.
и построить ее график.
Решение.
Область определения функции

Функция не является четной или нечетной.
Функция не является периодической

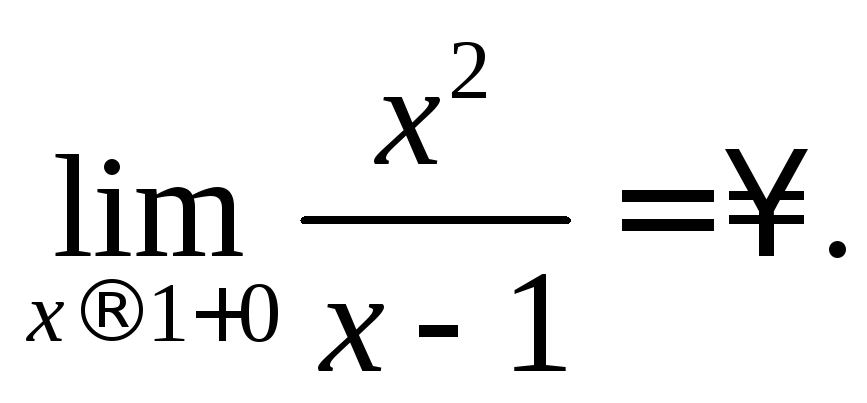
Прямая
![]() является вертикальной асимптотой.
является вертикальной асимптотой.
 Возможна наклонная
асимптота, так как
Возможна наклонная
асимптота, так как

 Тогда
Тогда и
и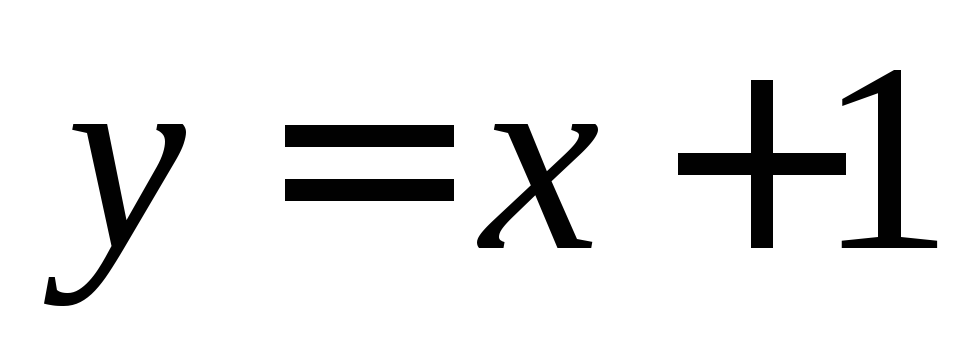 является наклонной асимптотой.
является наклонной асимптотой.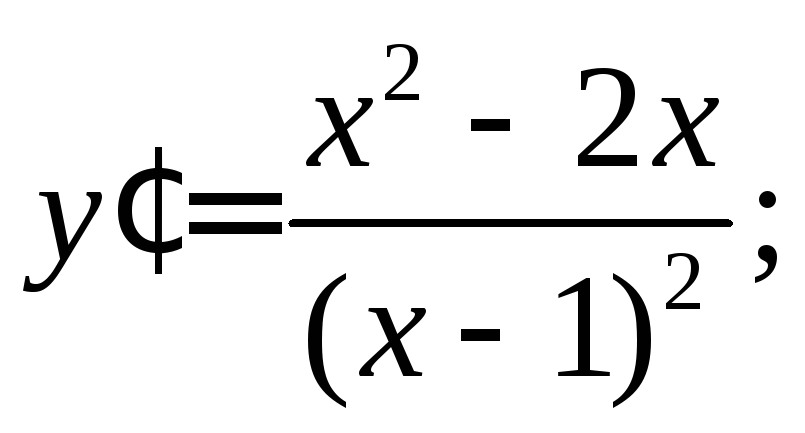
 при
при
 и
и Покажем знаки производной:
Покажем знаки производной:
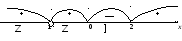
знак
![]()
поведение y
На множестве
![]() функция возрастает. На множестве
функция возрастает. На множестве![]() функция убывает. Точка
функция убывает. Точка![]() является точкой локального максимума,
а точка
является точкой локального максимума,
а точка![]() является точкой локального минимума.
Значения функции в точках экстремума
является точкой локального минимума.
Значения функции в точках экстремума![]()
![]()

 решения нет. При
решения нет. При
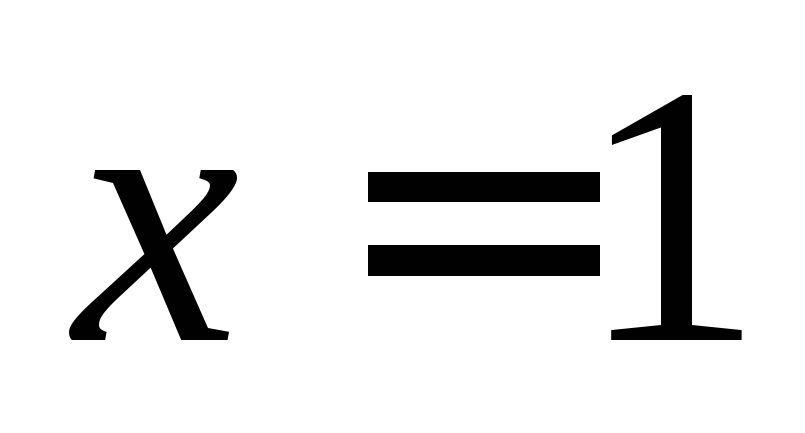 вторая производная не определена, но
в этой точке и сама функции не определена.
Укажем знак второй производной:
вторая производная не определена, но
в этой точке и сама функции не определена.
Укажем знак второй производной:

знак
![]()
поведение y
На множестве
![]() график функции выпуклый вверх, а на
множестве
график функции выпуклый вверх, а на
множестве![]() график функции выпуклый вниз. Точек
перегиба нет.
график функции выпуклый вниз. Точек
перегиба нет.
Точка пересечения с осями единственная – начало координат

Нарисуем график функции

►
6.3.
Исследовать функцию
![]() и построить ее график.
и построить ее график.
Решение.
1. Функция определена
на множестве
![]()
2. 3. Исследование на четность и периодичность не проводится.
4. Функция непрерывна на области определения.
5.
![]() и
и![]() является вертикальной асимптотой.
является вертикальной асимптотой.
![]() Поэтому
Поэтому
![]() является горизонтальной асимптотой.
является горизонтальной асимптотой.
6.
![]()
![]() при
при![]() Покажем знаки производной:
Покажем знаки производной:

знак
![]()
поведение y
Функция возрастает
на интервале
![]() и убывает на множестве
и убывает на множестве![]() Точка
Точка![]() является точкой максимума,
является точкой максимума,![]()
7.
![]()
![]() при
при![]() Определяем знак второй производной:
Определяем знак второй производной:

знак
![]()
поведение y
График функции
выпуклый вверх на множестве
![]() и выпуклый вниз на множестве
и выпуклый вниз на множестве![]() Точка
Точка![]() является точкой перегиба,
является точкой перегиба,![]()
8.
![]() при
при![]()
Построим график функции

Исследовать функции и построить их графики:
