38

Пособие по математике

ТЕМА «ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ»

СОДЕРЖАНИЕ

Введение 4

Глава 1. Производная 5

§ 1 Определение производной. 5

§ 2. Правило дифференцирования. Таблица дифференцирования основных элементарных функций. 7

§ 3.Геометрическое, механическое и экономическое приложения производной. 16

§ 4.Задачи для самостоятельной работы. 19

Глава 2 Приложения производной. 21

§ 1.Дифференциал функций. 21

§ 2.Правило Лопиталя. 23

§ 3.Возрастание и убывание функций. Экстремум функции. 24

§ 4.Наибольшее и наименьшее значения функции на отрезке. 28

§ 5.Выпуклость графика функции. Точки перегиба. 29

§ 6.Исследование функций и построение их графиков. 31

§ 7.Задачи для самостоятельной работы. 36

ВВЕДЕНИЕ

Данная работа предназначена для студентов экономических специальностей ТГУСа; может быть полезна для всех категорий студентов, изучающих курс «Математика». Рассматривается раздел «Дифференциальное исчисление». В данной части излагаются темы: производная, приложение производной.

В каждом параграфе изложен теоретический материал, содержатся типовые задачи с решениями и для практических заданий, позволяющие достаточно полно охватить учебный материал. В последних параграфах каждой главы приводятся задачи для самостоятельного решения. В работе имеется подборка заданий для расчетно-графической работы по разделу «Дифференциальное исчисление». Кроме того, излагается тестовый материал для самостоятельной проверки усвоения знаний.

Пособие должно помочь студенту для самостоятельного изучения материала, когда он что-то не усвоил на практических занятиях, какие-то занятия пропустил.

Нумерация задач единая по каждой главе. Конец решения задачи обозначается знаком ►.

Глава 1. Производная

§1. Определение производной.

1. Пусть функция определена на интервале. Аргументузададим приращение, соответствующее приращение функции.

Производной функции в точкеназывается предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю (предполагается, что этот предел существует и конечен).

Производную функции обозначают одним из символов.

Производная функции в точке может быть вычислена по одной из формул:

;

;

2. Функция, имеющая производную в каждой точке интервала называетсядифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.

Значение производной функции в точкеобозначается одним из символов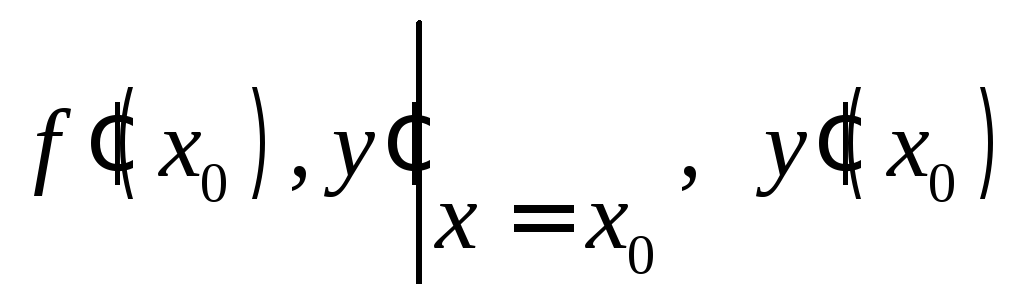

3. Если функция дифференцируема в точке(или на множестве), то она в этой точке (или на множестве) непрерывна. Если функция непрерывна в точке, то она не обязательно дифференцируема в этой точке.

1.1. Используя определение производной, найти производную функции .

Решение. Придавая аргументу приращение, найдем приращение функции:

.

Найдем предел отношения приращения функции к приращению аргумента при :

.

Таким образом: . ►

1.2. Доказать, что функция непрерывна, но не дифференцируема в точке .

Решение.

1. Функция определена на всей числовой оси, причем . Предел функциипри, стремящимся к нулю, равен значению функции в нуле:. Поэтому функциянепрерывна в точке

2.Составим отношение

Производная функции в точке

.

Предел зависит от знака :

,

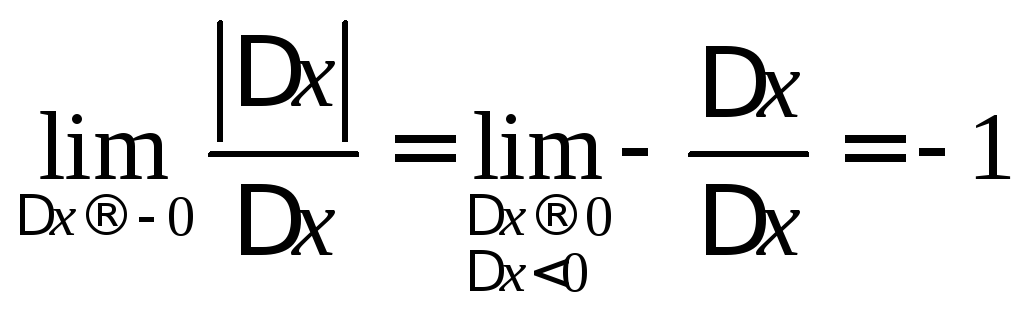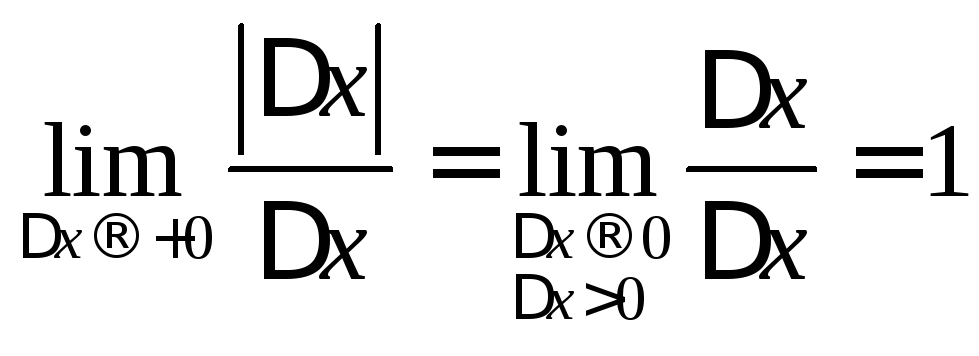
Тогда . Поэтомуне существует и функциине дифференцируема в точке►

1.3. Доказать, что функция не дифференцируема в точке.

Решение. Функция определена в любой окрестности точки. Производная функции

т.е. функция не является дифференцируемой в точке . ►

Используя определения производной, найти производную функций;

1.4.1.6.

1.5. 1.7.

Доказать, что функция непрерывна и дифференцируема при

1.8.1.9.