3.1. Визначення вихідного опорного плану

У наступному прикладі розглядається один з можливих алгоритмів одержання опорного плану.

Задача 3.1. Знайти вихідний опорний план для задачі

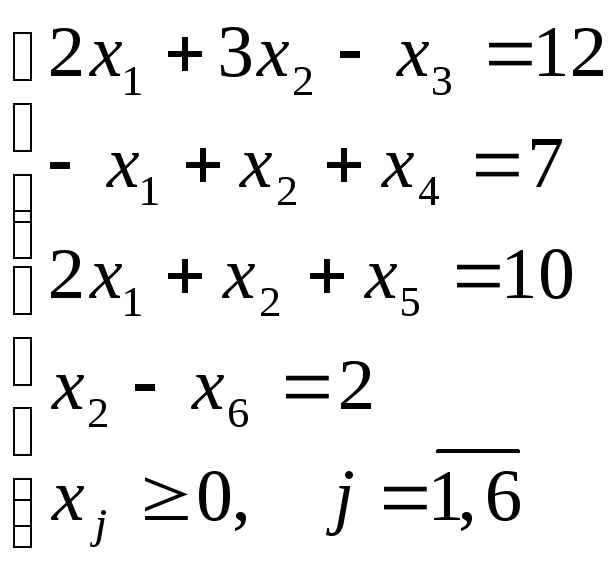
Рішення

Дана задача подана у канонічному виді. Побудуємо вихідний опорний план. З коефіцієнтів при змінних і вільних членах рівнянь системи обмежень складаємо розширену матрицю (її j-й стовпець відповідає вектору-стовпцю коефіцієнтів при змінній x_j (j=1,2,3,4,5), останній стовпець – вектору-стовпцю вільних членів). Приводимо дану матрицю до одиничного базису (за допомогою елементарних перетворень рядків матриці виділяємо максимальну кількість попарно різних одиничних векторів-стовпців). Помножимо перший і четвертий рядки на (–1):

.

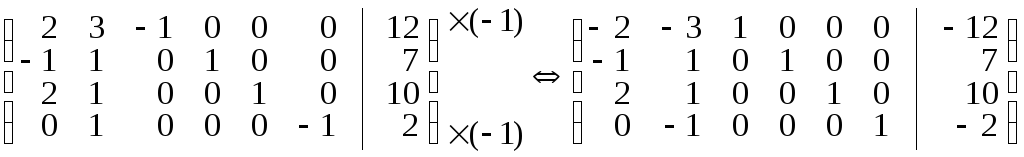Змінні, яким відповідають одиничні вектори-стовпці у перетвореній матриці, будемо вважати базисними, інші змінні – вільними.

У нашому випадку

I крок. Базисні змінні: x₃, x₄, x₅, x₆; вільні змінні: x₁, x₂.

Тому базисний розв’язок (у силу його визначення): . Цей розв’язок не є допустимим, тому що він містить дві від’ємні компоненти (виділені).

Знаходимо новий базисний розв’язок. Визначаємо базисну змінну, що виводиться з базису, і вільну змінну, що вводиться замість неї до базису. Для цього розглянемо рядки матриці, де містяться від’ємні вільні члени і(перший і четвертий), і від’ємні коефіцієнти при вільних зміннихx₁ і x₂ у цих рядках: ,, . Знаходимо

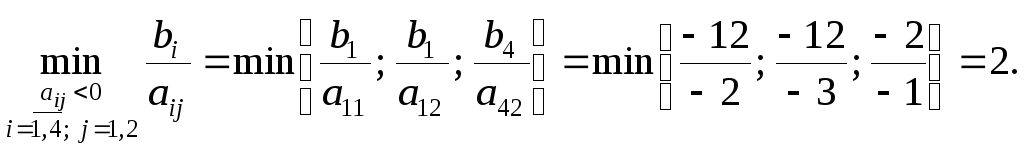
Мінімум досягається на елементі . Цей елемент будеключовим. Його перший індекс визначає ключовий рядок IV (який вказує на базисну змінну x₆, що виводиться з базису), другий індекс – ключовий стовпець II (змінну x₂, що вводиться до базису). За допомогою елементарних перетворень рядків матриці в стовпці II будуємо одиничний вектор, в якому 1 знаходиться в рядку IV. (Помножимо рядок IV на (–1), одержимо . Потім додамо до рядка I рядок IV, помножений на 3, і віднімемо з рядків II і III рядок IV).

.

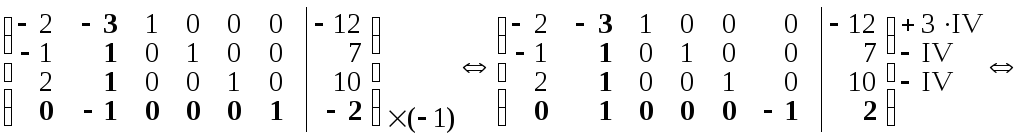
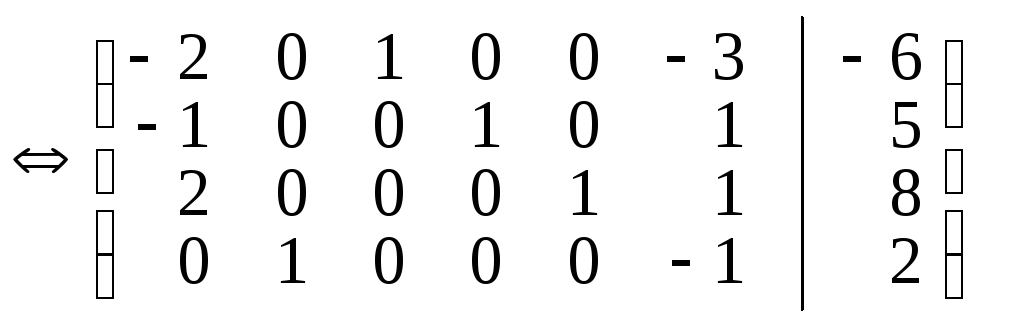Після перетворення

II крок. Базисні змінні: x₂, x₃, x₄, x₅; вільні змінні: x₁, x₆.

Тому базисний розв’язок: . Цей розв’язок не є допустимим, тому що він теж містить від’ємну компоненту.

Знову виконуємо перетворення. Рядок I (з від’ємним вільним членом ) має від’ємні коефіцієнти при вільних зміннихx₁ і x₆ у цьому рядку: ,. Знаходимо

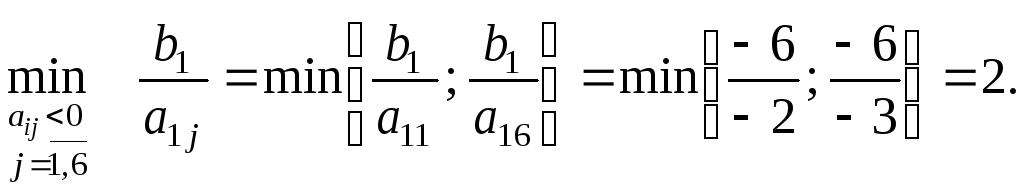
Мінімум відповідає елементу , тому базисною змінною, що виводиться з базису, єx₃ (третій стовпець містить одиничний вектор, в якому 1 розташована у ключовому рядку I), вільною змінною, що вводиться до базису, є x₆. За допомогою елементарних перетворень у стовпці VI будуємо одиничний вектор, в якому 1 розташована в рядку I.

.

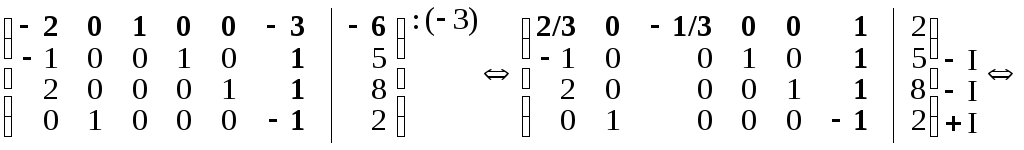
Після другого перетворення

III крок. Базисні змінні: x₂, x₄, x₅, x₆. Вільні змінні: x₁, x₃.

Базисний розв’язок: . Цей розв’язок вже є опорним планом задачі, тому що всі його компоненти невід’ємні.

Зауваження 3.1. Якщо базисний розв’язок не є допустимим, а в рівнянні, що містить від’ємний вільний член, немає вільної змінної з від’ємним коефіцієнтом, то в цьому випадку опорний план одержати неможливо, тобто умови задачі суперечливі.